Mg-Ti-H体系晶体结构与相稳定性的第一性原理计算

杜晓明 李武会 黄 勇 吴尔冬

(1沈阳理工大学材料科学与工程学院,沈阳110159;2中国科学院金属研究所,沈阳110016)

Mg-Ti-H体系晶体结构与相稳定性的第一性原理计算

杜晓明1,*李武会2黄 勇1吴尔冬2

(1沈阳理工大学材料科学与工程学院,沈阳110159;2中国科学院金属研究所,沈阳110016)

采用基于密度泛函理论的第一性原理赝势平面波方法计算了不同Ti含量的MgxTi(1-x)H2(x=0.25,0.5, 0.75,0.875)体系的平衡晶格结构、总能量及稳定性.结果表明:氢原子在晶胞中的位置接近于四面体间隙位置;H―Ti原子间距小于H―Mg原子间距,表明Ti较Mg具有更强的“亲氢性”,Ti原子在吸引周围H原子的同时削弱了H―Mg键的强度;随Ti含量的增加,体系的稳定性和脱氢温度均降低,且MgxTi(1-x)H2体系与MgH2相比,稳定性更差,脱氢温度更低,表明Ti可降低MgxTi(1-x)H2体系的分解温度并加速其脱氢动力学过程,表现出脱氢催化活性.

MgxTi(1-x)H2; 晶体结构; 赝势平面波; 稳定性

1 引言

Mg及其合金因其密度小、储氢能力高(7.6%)、价格低、储量丰富而使之成为一种很有前途的储氢合金.1然而镁基合金储氢的主要缺点是吸放氢温度高(＞300°C),吸放氢速度较慢,反应动力学和热力学性能较差,严重妨碍了氢的吸附,这些缺点都成为其实用化的障碍.近年来国内外众多研究人员为发展高性能镁基储氢材料从实验和理论方面开展了广泛的研究.多数研究表明,在镁基合金中添加部分过渡族金属元素可有效改善其吸放氢动力学性能.2-4最近,Choi等5通过研发摩尔比分别为7:1和4:1的MgH2+TiH2混合物的高能球磨发现,该体系的脱氢温度在399-586 K之间.Vermeulen等6在纯镁中加入金属Ti后,Mg-Ti合金薄膜的储氢量可达到5.3%(w).为了揭示Ti对镁基合金储氢过程的热力学及动力学性能的影响机制,Song等7采用全势线性平面波(FLAPW)方法计算了Ti固溶于MgH2时合金稳定性的变化,发现合金化后体系的相稳定性变差,并由此预测Ti具有改善MgH2的脱氢动力学行为的作用.Xiao等8的计算结果表明,Mg7TiH16的脱氢温度低于MgH2的原因是Ti与氢原子间形成的强烈共价键,削弱了Mg与氢原子间的作用.张健等9进一步计算了Ti掺杂MgH2体系的脱氢性能,也表明掺杂Ti后体系相稳定性降低.

尽管人们针对添加过渡金属元素改善MgH2体系的脱氢性能做了一定的实验和理论探索,却没有系统研究不同含量Ti固溶于MgH2体系中形成Mg-Ti-H体系的相稳定性及Ti对该体系脱氢难易程度的影响.本文采用基于密度泛函理论的第一性原理赝势平面波方法,构造不同含Ti量的Mg-Ti-H超晶胞模型,系统研究Mg-Ti-H体系的几何构型、相稳定性及脱氢动力学性能,为改善镁基合金的储氢性能提供理论指导.

2 计算方法与模型

2.1 计算方法

计算采用Quantum-ESPRESSO10第一性原理密度泛函量化软件包.Quantum-ESPRESSO是基于密度泛函理论的第一性原理平面波赝势方法.11采用周期性边界条件,晶体波函数由平面波基组展开.计算过程中原子赝势采用超软赝势12计算,交换关联势采用广义梯度近似(GGA)13处理.动能截断点取310.0 eV,总能量计算采用自洽迭代(SCF)法.k点网格数如下:对于MgH2晶胞,取12×12×16;对于TiH2晶胞,取12×12×12;对于MgxTi(1-x)H2晶胞,取8×8×8.计算Mg、Ti、H的赝波函数分别为Mg 2p63s2,Ti 3s23p63d24s2和H 1s1.采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法对所有晶胞模型进行结构优化,以求得它们的局域最稳定结构.结构优化时,总能量的收敛值取2.0×10-5eV·atom-1,每个原子上的力低于0.05 eV-1,应力偏差小于0.1 GPa.

2.2 计算模型

MgH2晶体结构如图1(a)所示,晶格常数a= 0.4501 nm,c=0.3010 nm,空间群为P42/mnm,晶胞中各原子坐标为:+2Mg:(0,0,0);+4H:(0.304,0.304, 0).14TiH2的晶体结构如图1(b)所示,晶格常数a= 0.4454 nm,空间群为Fm3m,晶胞中各原子坐标为: +4Ti:(0,0,0);+8H:(0.25,0.25,0.25).15对于MgxTi(1-x)H2(x=0.25,0.5,0.75和0.875)晶体结构,目前仅有Mg7TiH16结构(即Mg0.875Ti0.125H2)在高温高压条件下合成出来,具有Ca7Ge晶体结构(a=0.9535(2) nm,空间群为Fm3m),晶胞中有96个原子,H原子占据四面体间隙位置.16我们以此为起点来构建本研究中的MgxTi(1-x)H2晶体结构.对于x=0.875的结构,采用Ca7Ge晶体结构确定金属原子位置.对于x= 0.25,0.75,采用Cu3Au(L12)结构,而对于x=0.5,采用CuAu(L10)结构.在以上所有结构中,H原子置于四面体间隙位置附近.四种MgxTi(1-x)H2超晶胞模型分别如图1(c,d,e,f)所示.

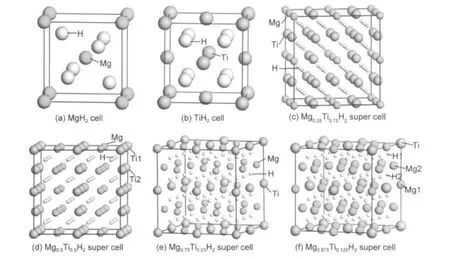
图1 计算所用模型Fig.1 Models of calculation

3 计算结果与讨论

3.1 氢化物结构及总能量

首先计算了单质金属Mg、Ti,气态H2分子及MgH2和TiH2晶胞的晶格常数和总能量.计算结果列于表1.由表1可见,计算所得Mg、Ti的平衡晶格常数,气态H2分子键长及MgH2和TiH2晶胞参数均与实验值15,17-20符合得较好.表明本文所用的计算模型及计算方法合理.此外,表1也给出了上述各种单质及化合物的总能量的计算结果.

然后采用相同的计算条件分别对x=0.25,0.5, 0.75,0.875四种MgxTi(1-x)H2超晶胞模型进行几何结构优化.所得各模型的平衡晶格常数、晶胞体积、总能量及原子坐标列于表2和表3中.由表2可知,除Mg0.5Ti0.5H2外,其余三种结构都属于立方晶系. Rousselot等21采用高能球磨法制备的Mg0.5Ti0.5二元亚稳态合金的晶体结构为密排六方相结构(空间群为P63/mmc,晶格常数a=0.303 nm,c=0.484 nm),而经过吸氢后,氢化物结构转变为面心立方结构.而Pauw等22采用密度泛函理论计算Mg0.5Ti0.5H2结构为金红石型结构,与本文的计算结果接近.此外,随Ti含量的增加,四种晶胞模型的晶格常数变小,这是由较小的Ti原子固溶于较大的Mg晶格中引起了晶格收缩.这一点从四种结构的晶胞体积计算值(表2)也得到了证实,即随晶胞中Ti原子数的增加,晶胞体积发生收缩.在实验中也观察到了这种变化, Liang和Schulz23采用球磨法制备的Mg-Ti二元合金中发现Ti固溶于Mg晶格中引起了Mg晶格的收缩. Mitchell等24采用物理气相沉积法制备的六方晶格Mg-Ti合金也发现随Ti含量的增加,晶格常数a、c及a/c均变小.但他们认为这种变化是由原子尺寸因素和价电子因素共同作用的结果.通过比较表2中Mg0.875Ti0.125H2结构晶格常数的计算值和实验值16可知,计算值比实验值偏小1.3%.分析其原因,本文的理论计算结果是绝对零度下的晶体几何结构参量;而实验数据则来自有限温度下的实验测试.因此,两者之间存在差异是必然的.这一点从表1中MgH2和TiH2的计算值与实验值之间的差异也得到了证实.总之,对MgxTi(1-x)H2晶体系统的几何结构优化结果表明,所用的理论方法是可靠的.利用此种方法计算其他体系的物理性质可为我们提供有价值的参考数据.

对MgxTi(1-x)H2晶体(x=0,0.25,0.5,0.75,0.875,1)系统而言,MgH2和TiH2是两个极端情况.将MgH2和TiH2的单胞能量值折算成超晶胞能量值后(见表1),以MgH2和TiH2的超晶胞能量值为端点连线,如图2所示.再将各MgxTi(1-x)H2晶体(x=0.25,0.5,0.75, 0.875)系统的能量值(见表2)标于图2中,这些点基本上位于连线的两侧.由此可见,这六个晶体系统的总能量基本为线性关系.

表1 Mg、Ti、H2气态、MgH2和TiH2的平衡晶格常数和总能量Table 1 Equilibrium lattice constants and total energy of Mg,Ti,H2(gas),MgH2,and TiH

表2 四种MgxTi(1-x)H2晶胞模型几何优化后的平衡晶格常数、晶胞体积及总能量Table 2 Optimized equilibrium lattice constants,cell volume and total energy of four MgxTi(1-x)H2structures

表3 四种MgxTi(1-x)H2超晶胞模型结构优化后的原子位置Table 3 Optimized atomic positions of four MgxTi(1-x)H2supercells

图2 总能量(Etot)与Mg含量(xMg)的关系Fig.2 Relationship between total energy(Etot)and Mg content(xMg)

表3给出了四种MgxTi(1-x)H2超晶胞结构优化后的原子位置.从表3可以看出,本文计算所得的Mg0.875Ti0.125H2结构中金属原子的位置与实验中确定的位置吻合得较好,而氢原子的位置与实验值稍有偏差,其绝对偏差值为0.01-0.02 nm.这一偏差对于确定氢原子的位置几乎没有影响,因为在进行结构优化时不论采用实验晶格参数还是计算所得的晶格参数,所得的氢原子的位置是相同的.另外,从TiH2和MgH2晶胞中氢原子占据四面体间隙位置来看,15,16比较表3中四种MgxTi(1-x)H2晶胞中氢原子的位置可知,这四种晶胞中氢原子的位置接近于四面体间隙位置.Kyoi等25对高压合成的Mg7TiHx结构的XRD精细结果表明,晶胞中的氢原子并未占据理想的四面体位置,而是一种变形的四面体间隙位置.Pauw等22在采用密度泛函理论计算Mg-TM (TM=Sc,Ti,Zr,Hf)氢化物结构时认为,氢化物中氢原子明显偏离了理想四面体间隙位置,最大偏移量为14.8%,是一种变形的四面体间隙位置.然而Kohta等26对球磨法制备的Mg-Ti-H化合物(FCC结构)的晶体结构分析时认为,Mg-Ti-H化合物中的氢原子位置与TiH2中的氢原子位置相同,都占据四面体间隙位置.从上述文献的研究结果看,本文的研究结果与Kyoi等和Pauw等的结果相符.

由表3可知,氢原子在Mg0.875Ti0.125H2结构中占据两种四面体间隙位置,而在其余三种Mg-Ti-H结构中仅有一种四面体间隙位置.对于Mg0.875Ti0.125H2结构,H1原子占据由Ti原子和3个Mg2原子形成的四面体间隙,其中H1原子与Ti原子和Mg2原子的距离分别为0.1952和0.2076 nm,而实验值分别为0.1557和0.2293 nm;16H2原子占据由Mg1原子和3个Mg2原子形成的四面体间隙,其中H2原子与Mg1原子和Mg2原子的距离分别为0.2083和0.2076 nm,而实验值分别为0.2236和0.2021 nm.16对于Mg0.25Ti0.75H2、Mg0.5Ti0.5H2、Mg0.75Ti0.25H2结构中的H―Ti原子间距的计算值分别为0.1919、0.1931和0.1946 nm.在TiH2中H原子占据理想的四面体间隙位置,且H―Ti原子间距为0.1916 nm.15本文中H―Ti原子间距的计算值为0.186-0.196 nm,与TiH2中H原子的四面体间隙位置接近,这也再次表明这四种结构中氢原子的位置接近于四面体间隙位置.图3给出了四种MgxTi(1-x)H2化合物(x=0.25,0.5,0.75, 0.875)中Ti含量对金属(Mg和Ti)与H原子间距的影响.由图3可知,随Mg-Ti-H结构中Ti含量的增加,H―Ti和H―Mg原子间距均减小,这与前述的晶胞体积减小结果一致.另外,从图3中也可知, MgxTi(1-x)H2结构中的H―Ti原子间距均小于H―Mg原子间距,并且MgH2结构中H―Mg原子间距也明显小于MgxTi(1-x)H2结构中的H―Mg原子间距,这表明Ti较Mg具有更强的“亲氢性”,氢原子在Ti原子的“吸引力”下向其靠近,却使H与周围临近Mg原子间距增大,从而削弱了H―Mg键的强度.

3.2 氢化物的形成焓

合金形成焓是衡量金属氢化物吸放氢性能的一个重要热力学参数,通过计算合金的形成焓,即可对金属氢化物的结构稳定性和放氢性能进行评价和预测,即氢化物的负合金形成焓越大,生成的氢化物稳定性越高,体系的放氢能力越差.为了研究Ti含量对MgxTi(1-x)H2结构相稳定性及放氢能力的影响,采用式(1)对MgH2、TiH2以及MgxTi(1-x)H2体系的每摩尔氢分子的合金形成焓ΔH进行计算:

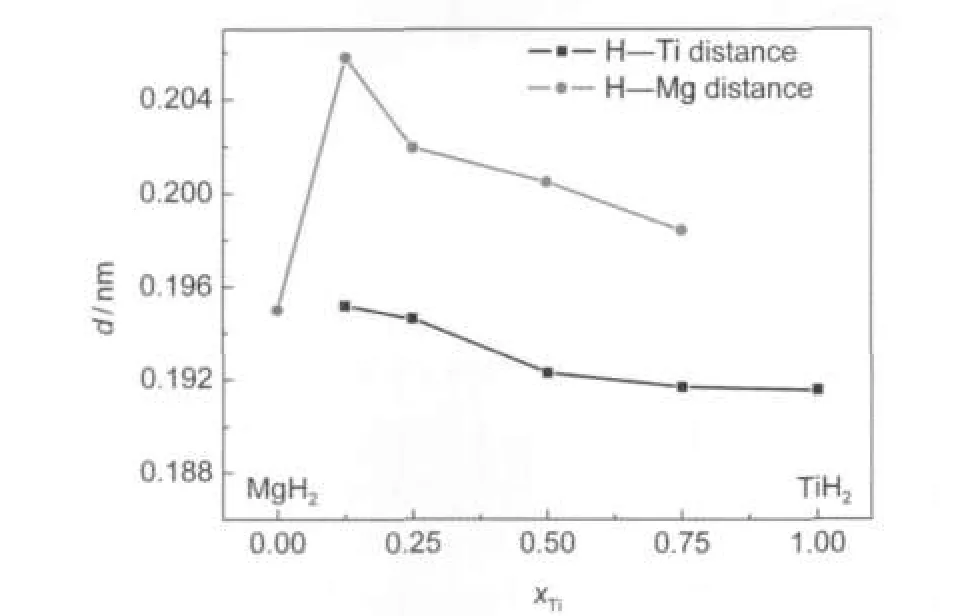
图3 金属-氢原子间距(d)与Ti含量(xTi)的关系Fig.3 Relationship between metal-hydrogen inter-atomic distance(d)and Ti content(xTi)

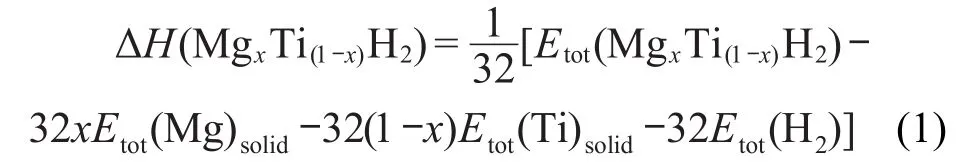
式中,Etot(MgxTi(1-x)H2)为MgxTi(1-x)H2超晶胞的总能量;x为氢化物中Mg的摩尔分数(x=1,0.875,0.75, 0.5,0.25,0);Etot(Mg)solid、Etot(Ti)solid、Etot(H2)分别为固态单质Mg原子、固态单质Ti原子、气体H2分子的总能量.Mg、Ti晶体单原子能量由晶胞总能量换算得到,计算结果见表1.H2分子总能量采用Barth-Hedin交换关联势函数27得到,计算值为-2.320 Ry (-31.5652 eV).由式(1)计算的不同氢化物形成焓结果列于表4.由表4可见,MgH2氢化物的形成焓的计算值为82.693 kJ·mol-1,而Bogdanović等28采用量热法在673 K测得的实验值为-73.5 kJ·mol-1,本文计算的MgH2氢化物的形成焓ΔH值比实验值略高,但与Yamaguchi和Akiba29的实验值(-66.95--85.35 kJ·mol-1)极为接近.文献30中报道的TiH2氢化物的形成焓的实验值为-1.30--1.50 eV(约为-125.37--144.66 kJ·mol-1),与本文表4中TiH2氢化物的形成焓的计算结果符合得很好.对于MgxTi(1-x)H2体系,氢化物的形成焓ΔH值在-56--47 kJ·mol-1范围,均低于MgH2的形成焓,且随Ti含量的增加,氢化物的形成焓呈现明显的下降趋势,这表明不同含量Ti固溶于MgH2中,使体系的相结构稳定性变差,有利于改善其放氢能力.这是由于Ti的加入改变了合金的晶格间隙环境,使氢化物分解更为容易.因此,较小的氢化物形成焓意味着氢化物生成时的氢能损失较少,这对于储氢合金的实际应用有非常重要的意义.周惦武等31计算的不同含量Ti固溶于MgH2后的形成焓为-54.29--41.29 kJ·mol-1,Song等7的计算值为-51.614 kJ·mol-1,由此可见,本文的计算结果较为可靠.

通过氢化物形成焓的计算,不但可以定性评价和预测氢化物相结构的稳定性,而且还可以定量估算氢化物的脱氢温度.氢化物的脱氢反应热力学过程可由Gibbs公式描述:

式中,ΔG、ΔH、ΔS分别为脱氢反应体系的标准吉布斯自由能、形成焓和熵变.由于在吸放氢反应中反应物和产物以固相为主,反应系统的压力与体积变化较小,因此在式(2)中忽略了外界功对体系吉布斯自由能的贡献.在氢化物分解温度及恒定压力条件下,体系的标准吉布斯自由能ΔG=0,因此脱氢温度为

由于固态材料在加热过程中的熵变与气体相比很小,因此脱氢反应过程的熵变以H原子向H2分子转变过程为主,即ΔS≈ΔS(H2).对于大多数简单金属氢化物体系(如MgH2、TiH2等),ΔS(H2)为130.7 J· K-1·mol-1,32而对于其他金属氢化物体系,ΔS(H2)在95-140 J·K-1·mol-1.33由式(3)计算的上述六种金属氢化物的脱氢温度列于表4中.由表4可知,在MgH2中加入Ti形成MgxTi(1-x)H2体系后,其脱氢温度与MgH2相比都明显降低,且随Ti加入量的增加, MgxTi(1-x)H2体系的脱氢温度呈现下降趋势,特别是对于Mg0.25Ti0.75H2,比MgH2的脱氢温度约低134-295 K.这表明Ti对MgxTi(1-x)H2体系的脱氢动力学起到催化作用,即降低其分解温度与加速其脱氢动力学过程.Kyoi等25测定的Mg7TiHx体系的脱氢温度实验值为605 K.Choi等5对研发摩尔比分别为7:1和4:1的MgH2+TiH2混合物的高能球磨发现,该体系的脱氢温度在399-586 K之间.与本研究中的Mg0.875Ti0.125H2和Mg0.75Ti0.25H2的脱氢温度较为接近.

表4 MgH2、TiH2和MgxTi(1-x)H2体系的氢化物形成焓和放氢温度Table 4 Formation enthalpy of hydrides and dehydrogenation temperature of MgH2,TiH2,and MgxTi(1-x)H2systems

4 结论

采用基于密度泛函理论的第一性原理赝势平面波方法,研究了不同Ti含量的MgxTi(1-x)H2体系的平衡晶体结构、总能量及结构稳定性,得到如下主要结论:

(1)对x=0.25,0.5,0.75,0.875四种MgxTi(1-x)H2超晶胞模型的结构优化结果表明,随着Ti含量的增加,晶胞体积和总能量均减小,且Mg0.875Ti0.125H2晶格参数的计算值与实验值符合得较好;氢原子在晶胞中的位置接近于四面体间隙位置,Ti的加入使H―Mg原子间距增大,表明Ti较Mg具有更强的“亲氢性”,Ti原子在吸引周围H原子的同时却削弱了H―Mg键的强度.

(2)氢化物的形成焓和脱氢温度计算结果表明: MgxTi(1-x)H2体系与MgH2相比,稳定更差,脱氢温度更低,随Ti含量的增加,MgxTi(1-x)H2体系的稳定性和脱氢温度呈现明显下降趋势,这表明Ti可降低MgxTi(1-x)H2体系的分解温度并加速其脱氢动力学过程,表现出主要的脱氢催化活性.

(1) Schlapbach,L.;Zuttel,A.Nature 2001,414,23.

(2) Pelletier,J.F.;Huot,J.;Sutton,M.;Schulz,R.;Sandy,A.R.; Lurio,L.B.;Mochrie,S.G.J.Phys.Rev.B 2001,63,052103.

(3) von Zeppelin,F.;Reule,H.;Hirscher,M.J.Alloy.Compd.2002, 330-332,723.

(4)Yao,X.;Wu,C.;Du,A.;Lu,G.Q.;Cheng,H.;Smith,S.C.; Zou,J.;He,Y.J.Phys.Chem.B 2006,110,11697.

(5) Choi,Y.J.;Lu,J.;Sohn,H.Y.;Fang,Z.Z.J.Power Sources 2008,180,491.

(6)Vermeulen,P.;Niessen,R.A.H.;Notten,P.H.L.Electrochem. Commun.2006,8,27.

(7) Song,Y.;Guo,Z.X.;Yang,R.Mater.Sci.Eng.2004,A365,73.

(8)Xiao,X.B.;Zhang,W.B.;Yu,W.Y.;Wang,N.;Tang,B.Y. Physica B 2009,404,2234.

(9) Zhang,J.;Huang,Y.N.;Mao,C.;Long,C.G.;Shao,Y.M.;Fu, J.Q.;Peng,P.Acta Chim.Sin.2010,68,2077.[张 健,黄雅妮,毛 聪,龙春光,邵毅敏,付俊庆,彭 平.化学学报,2010, 68,2077.]

(10) Giannozzi,P.;Baroni,S.;Bonini,N.et al.Quantum-ESPRESSO,Revision V.4.1.2;Free Software Foundation,Inc.: Cambridge,MA,2010.

(11) Payne,M.C.;Teter,M.P.;Allan,D.C.Rev.Mod.Phys.1992, 64,1045.

(12) Vanderbih,D.Phys.Rev.B 1990,41,7892.

(13) Perdew,J.P.;Chevary,J.A.;Vosko,S.H.;Jackson,K.A.; Pederson,M.R.;Shingh,D.J.;Fiolhais,C.Phys.Rev.B 1992, 46,6671.

(14) Bortz,M.;Bertheville,B.;Bottger,G.;Yvon,K.J.Alloy. Compd.1999,287,L4.

(15) Smithson,H.;Marianetti,C.A.;Morgan,D.;de Ven,A.V.; Predith,A.;Ceder,G.Phys.Rev.B 2002,66,144107.

(16) Ronnebro,E.;Kyoi,D.;Kitano,A.;Kitano,Y.;Sakai,T. J.Alloy.Compd.2005,404,68.

(17)Walker,C.B.;Marezio,M.Acta Met.1959,7,769.

(18) Pawar,R.R.;Deshpande,V.T.Acta Crystallogr.1968,24A,316.

(19) Hou,Z.F.J.Power Sources 2006,159,111.

(20)Miwa,K.;Ohba,N.;Towata,S.;Nakamori,Y.;Orimo,S.Phys. Rev.B 2004,69,245120.

(21) Rousselot,S.;Bichat,M.P.;Guay,D.;Roue,L.J.Power Sources 2008,175,621.

(22) Pauw,B.R.;Kalisvaart,W.P.;Tao,S.X.;Koper,M.T.M.; Jansen,A.P.J.;Notten,P.H.L.Acta Mater.2008,56,2948.

(23) Liang,G.;Schulz,R.J.Mat.Sci.2003,38,1179.

(24) Mitchell,T.;Diplas,H.;Thakiropoulos,P.;Watts,J.F.; Matthew,J.A.D.Philos.Mag.A 2002,82,841.

(25) Kyoi,D.;Sato,T.;Rönnebro,E.;Kitamura,N.;Ueda,A.; Mikio,I.;Katsuyama,S.;Hara,S.;Noréus,D.;Sakai,T.J. Alloy.Compd.2004,372,213.

(26) Kohta,A.;Etsuo,A.J.Alloy.Compd.2009,481,L8.

(27) Nakamura,H.;Manh,D.N.;Pettifor,D.G.J.Alloy.Compd. 1998,281,81.

(28)Bogdanović,B.;Bohmhammel,K.;Christ,B.;Reiser,A.; Schlichte,K.;Vehlen,R.;Wolf,U.J.Alloy.Compd.1999,282, 84.

(29) Yamaguchi,M.;Akiba,E.Ternary Hydrides.In Materials Science and Technology;Cahn,R.W.;Hassen,P.;Kramer,E.J. Eds.;Wiley-VCH:New York,1994;pp 333-345.

(30) Süleyman,E.;van Michiel,J.S.;de Gilles,A.W.;Geert,B. Phys.-Condens.Matter 2010,22,074208.

(31) Zhou,D.W.;Peng,P.;Liu,J.S.Chinese Journal of Nonferrous Metals 2005,15,1403.[周惦武,彭 平,刘金水.中国有色金属学报,2005,15,1403.]

(32) Zeng,Q.;Su,K.;Zhang,L.;Xu,Y.;Cheng,L.;Yan,X.J.Phys. Chem.Ref.Data 2006,35,1385.

(33)Alapati,S.V.;Johnson,J.K.;Sholl,D.S.J.Phys.Chem.B 2006,110,8769.

May 20,2011;Revised:August 22,2011;Published on Web:September 21,2011.

First-Principles Calculation of the Crystal Structure and Stabilization of Mg-Ti-H System

DU Xiao-Ming1,*LI Wu-Hui2HUANG Yong1WU Er-Dong2
(1School of Material Science and Engineering,Shenyang Ligong University,Shenyang 110159,P.R.China;2Institute of Metal Research,Chinese Academy of Sciences,Shenyang 110016,P.R.China)

First-principles calculations were performed to determine the equilibrium crystal structures, energetic properties,and stability of MgxTi(1-x)H2(x=0.25,0.5,0.75,0.875)systems containing different amounts of titanium using the pseudopotential plane-wave method based on density functional theory.The calculation results show that the hydrogen atoms in the MgxTi(1-x)H2hydrides roughly occupy the tetrahedral interstitial sites.The calculated H―Ti distances are less than the H―Mg distances.This indicates that Ti has a more notable affinity for hydrogen than Mg.The bonding strength of H―Mg is weaker when the Ti atom attracts surrounding hydrogen atoms.The stabilization and dehydrogenation temperatures of the hydrides MgxTi(1-x)H2are lower than those of MgH2with an increasing Ti content.This indicates that titanium can reduce the decomposition temperature of the MgxTi(1-x)H2hydrides and play a significant catalytic role in improving the dehydrogenation dynamic properties of the MgxTi(1-x)H2hydrides.

MgxTi(1-x)H2;Crystal structure;Pseudopotential plane-wave;Stabilization

10.3866/PKU.WHXB20112793

∗Corresponding author.Email:du511@163.com;Tel:+86-13019333439.

The project was supported by the Scientific Research Starting Foundation for Doctoral Program of Liaoning Province,China(20091066).

辽宁省博士启动基金(20091066)资助项目

O641;TF123.7