曲面加工中行距对表面粗糙度影响的研究

宋 新，马卫东

（黄河水利职业技术学院，河南 开封 475004）

0 引言

随着数控加工技术在机械加工行业的广泛应用， 数控铣床及加工中心等设备被广泛应用于复杂曲面的铣削加工。 在使用球头铣刀铣削曲面的数控加工中，除了切削用量、鳞刺、积屑瘤、刀具变形等因素对表面粗糙度Ra有很大影响之外， 行距对零件加工的表面粗糙度也有很大影响。 研究了球头铣刀在加工曲面时切削行距与表面粗糙度的关系。

1 行距的计算

在复杂曲面的加工中，行切法是有效的加工方法之一。 但行距的大小是影响加工表面质量和加工效率的重要因素，在加工之前一般需要确定[1]。

1.1 行距S 的一般计算方法

铣刀半径的确定与曲面曲率有关，尤其是在加工凹面时，铣刀半径必须小于凹面的曲率半径。 在进行铣削加工时，行距S 又与刀具半径r刀和刀锋高度h 有关[2]。 图1 为球头铣刀加工曲面的简图。

由图1 可以看出：

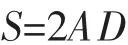
而

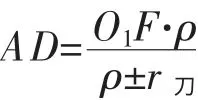
在空间曲面加工中，有时球刀半径r刀与要加工的曲面曲率半径ρ 有较大差异。 此时， 要想得到较小的刀锋高度h 和较好的表面质量，O1F 可取近似值，即：

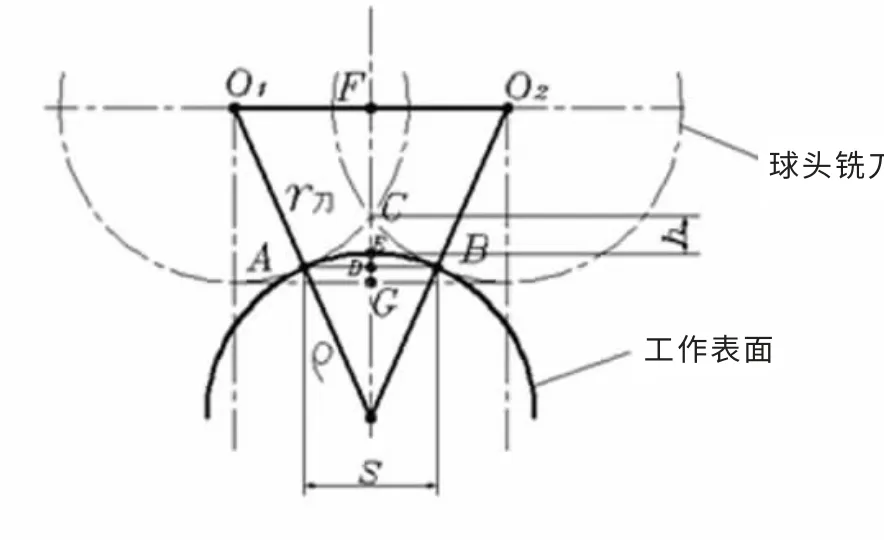
图1 球头铣刀加工曲面简图Fig.1 Ball milling cutter process curve

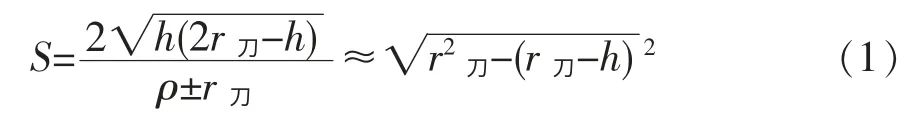
式中：r刀为球头铣刀刀具半径；S 为刀具切削时的行距；h 为刀峰间残留高度；ρ 为曲面曲率半径。

由上式可知，在加工空间曲面时，要想得到较好的表面质量和较高的加工精度，必须取最小的行距。

1.2 复杂曲面最小行距的确定

由上述可知，在曲面曲率半径最小的地方，行距要求最小。 对于空间复杂曲面，数据处理的工作量较大，通常可用CAM 软件分析得到曲面的最小曲率半径，从而节省大量的时间。

在边界混合曲面中，可利用Pro/Engineer 软件求出边界混合曲面的最小曲率半径[3]。 具体方法为：（1）创建边界混合曲面（建模）。 （2）选择主菜单中的分析→几何→曲率。 得到最小曲率半径后，可通过公式（1）求得实际加工中所需的最小行距。

在图2 所示的边界混合曲面，想得到曲面的加工表面粗糙度Ra为3.2 μm，则可取h＝0.0032 mm。若球头刀半径r刀＝5 mm, 求出曲面最小曲率半径为50.357 mm。 利用公式（1）可求出最小行距。

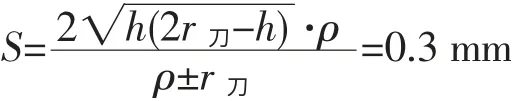
图2 边界混合曲面简图Fig.2 Boundary mixed curve

2 行距对表面粗糙度的影响

2.1 实验条件

机床采用四川自贡KV650 数控铣床，工件材料为铝合金,铣削方式为平行铣削（双向行切）,主轴可无级变速，主轴最大转速为6 000 r/min。 球头刀直径为10 mm，机床转速为3000 n(r/min)，X、Y 向F 值为300 mm/min，Z 向F 值为100 mm/min，精加工背吃刀量为1mm。

2.2 实验结果

当切削速度、进给量、背吃刀量不变时，实验数据如表1 所示。

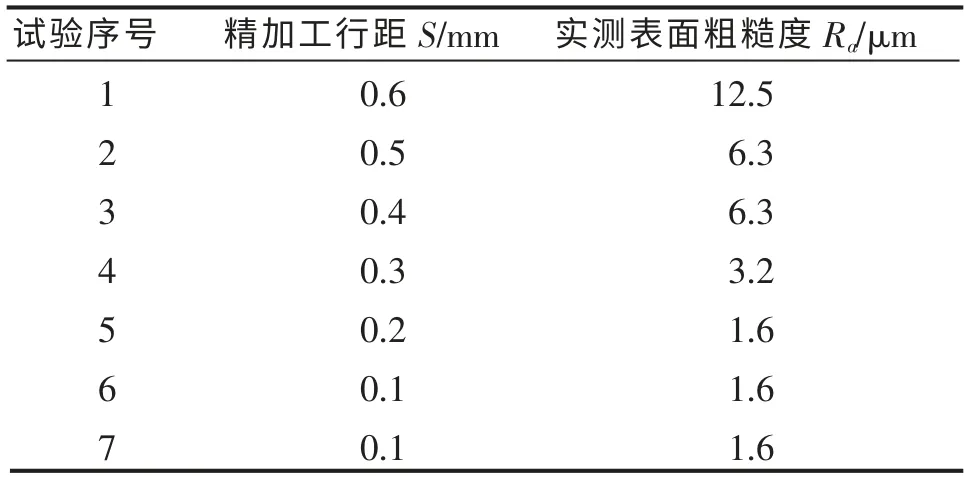
表1 行距对表面质量的影响Tab 1 Effect of line spacing to surface quality

与表1 对应的实验数据影像资料如图3 所示。

2.3 结果分析

当切削速度、进给量、背吃刀量、刀具半径不变时，通过以上数据，可以得到曲面行切加工时行距对表面粗糙度的影响曲线（如图4 所示）。 通过实验不难看出，当行距不断减小时，表面粗糙度的值也随之降低，但当降低到一定数值之后，表面粗糙度的值将不再随着行距的减小而降低。

图3 表面粗糙度影像Fig.3 Surface roughness image

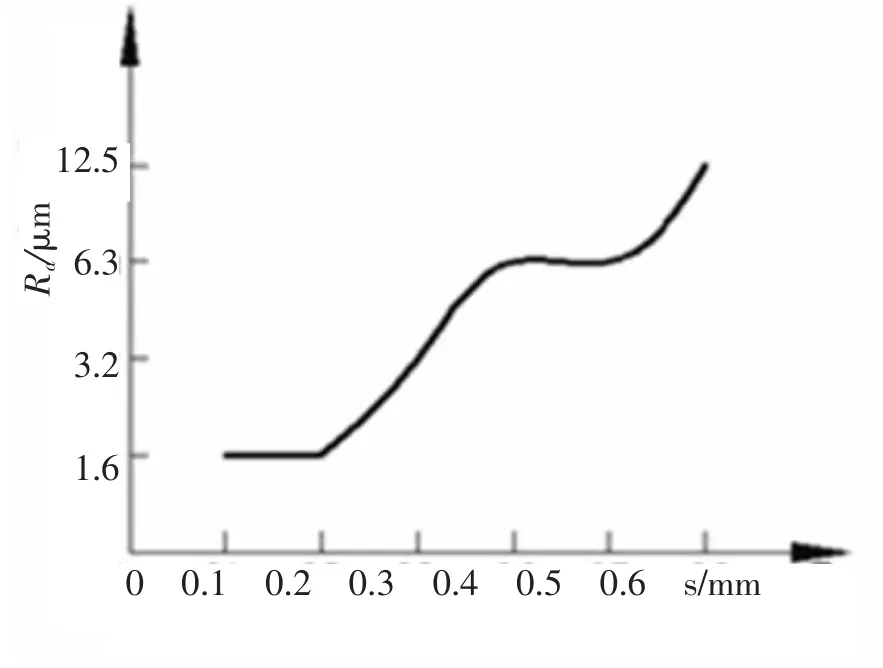
图4 行距与表面粗糙度的关系Fig.4 Relations of line spacing and surface roughness

3 结语

在空间曲面的数控加工过程中，随着行距的减小，表面粗糙度值随之减小，表面精度也越高。 但行距减小到一定程度，表面粗糙度值将不再减小。 从工艺及加工效率方面考虑，在粗加工时，行距S 可选得大一些，精加工时可选得小一些[5]。 有时为了减小刀峰高度h，行距S 可取经验值：0.7 倍的刀具直径，这样，实际效果会更好些。

[1] 张伯霖，杨庆东. 高速切削技术及应用[M]. 北京：机械工业出版社，2003：11-23.

[2] 施维. 高速切削加工技术的应用[J]. 煤矿机械，2005（5）：18-20.

[3] 汤宏群， 苏广才. 基于Pro/ E 的复杂曲面分模面构建方法研究[J]. 机械研究与应用，2004（1）：17-18.

[4] Juan Diego Frutos3 ,Denis Borenstein. A framework to supportcustomer2companyinteraction in mass ustomization environ2 ments[J]. Computers in Industry, 2004（2）：58-60

[5] Liu chong,Donald Esterling.solid modeling of 4-axis wire EDM cut geometry [J].Computer-Aided Design,1997,29(12):803-810.