大锥角聚能装药射流形成及对钢靶侵彻的数值模拟*

胡晓艳,刘天生,王凤英

(中北大学化工与环境学院,太原 030051)

0 引言

大锥角罩装药侵彻孔直径大、深度相对较浅,常用于攻击舰船、混凝土等目标,或者用于多级战斗部的前级装药,为后级装药开辟侵彻通道,是目前国内外重点研究的内容之一[1-3]。因此,对大锥角聚能射流及其侵彻过程的研究具有十分重要的意义。许多学者都对大锥角聚能装药进行了研究,谭多望等人[4-5]介绍了大锥角罩装药的X光实验研究结果并给出了大锥角罩装药的理论计算方法。王成等人[6]对大锥角聚能装药射流形成及对多层靶侵彻进行了研究。黄风雷和张雷雷[7-8]对大锥角药型罩聚能装药侵彻混凝土进行了实验研究。

随着计算机软、硬件技术的不断发展,数值模拟在大锥角聚能装药研究中得到广泛应用。它是认识聚能射流及其对靶板侵彻过程的重要工具。它可以替代昂贵危险的实验,并获得具体而完整的信息。文中使用AUTODYN软件,研究大锥角聚能装药射流形成及侵彻钢板过程,对各过程进行分析并与实验结果相比较。

1 数值模拟

1.1 控制方程

在AUTODYN程序中,利用有限差分方法,将如下的基本方程结合初始边界条件进行求解[9]:

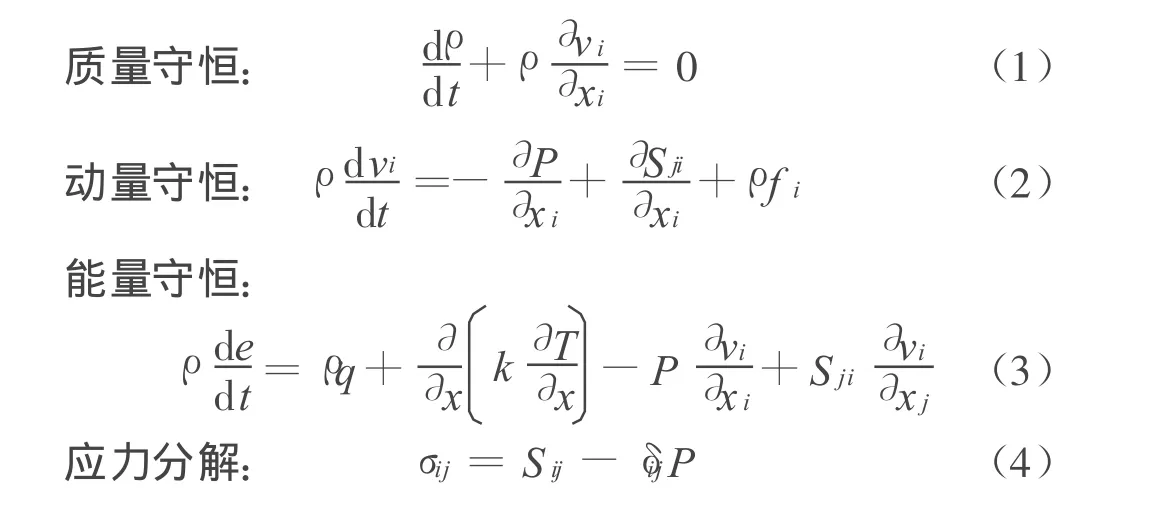
状态方程:

有限差分方法是利用显式时程积分来实现的。对于显式时程积分来说,它利用courant-friedrich-levy(CFL)准则来控制时间步长。CFL准则要求时间步长Δt小于声信号以速度c穿过网格空间Δx所需的时间。CFL准则可以表示为:

在高速撞击问题中,连续介质内会产生冲击波,这些冲击波在数学上是不连续的,这些不连续是出现在冲击区域内的超高频信号的根源。为了克服这个问题,在求解过程中,引入一个人工粘性来消除一些单元上的跳动,从而使程序继续计算得到一个光滑解。人工粘性用q来表示,它被添加到能量和动量方程中的静水压中进行计算,有如下形式:

式中:CQ和CL为常数,ρ为密度,d为特征长度(这里定义为区域的面积除以区域最长对角线),c为声速,为体积变化量。

1.2 材料模型及参数选取

计算中选用的炸药类型为8701炸药,材料模型为高能炸药爆轰模型,状态方程为JWL状态方程,其基本形式如下:

式中:P为压力;E0为初始比能;V为爆轰产物的相对体积;A、B、R1、R2和 ω为待定常数。8701炸药的计算参数如表1[10]。

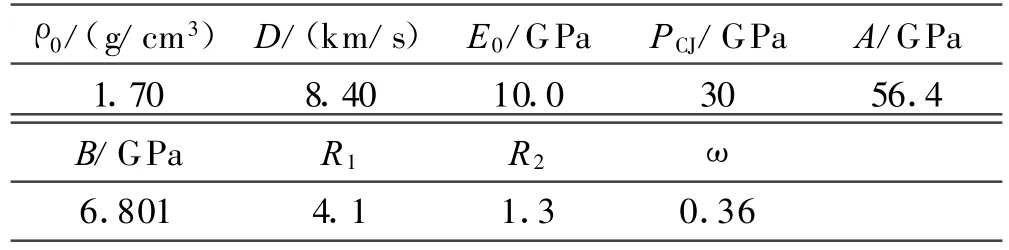
表1 8701炸药的计算参数

药型罩材料为紫铜,壳体材料为铝合金,靶板材料为钢,这些材料都采用Johnson-Cook材料模型以及Mie-Gruneisen状态方程描述其动态响应过程。材料模型参数取自AUTODYN数据库。

1.3 计算模型的建立

采用AUTODYN-2D程序建立标准模型,由于装药结构严格轴对称,可简化为1/4结构模型,然后再旋转360°成为3D模型。标准模型的初始条件为:药型罩锥角为150°,装药直径为60mm,装药高度为55mm,壳体厚度为 2mm,靶板为 35mm厚半径为40mm的圆柱。空气、炸药采用Euler多物质求解器进行求解,药型罩、壳体和靶板采用Lagrange求解器求解。起爆方式为环型起爆,起爆半径为10mm。标准模型如图1所示。

图1 标准模型图

2 大锥角聚能装药射流的特性分析

图2给出了大锥角聚能射流形成过程,由图2可知,在起爆20μs后,药型罩顶部已超过底部,此时顶部微元轴向速度明显大于底部微元的速度,药型罩为向后翻转成型。在起爆34μs后,药型罩向后反转完成,射流头部成型。起爆46μs后,射流中部拉伸和尾翼扩展完成,形成一个漏斗型的射流,这种射流头部具有较好的密实性和对称性。扩展的尾部使其具有较好的飞行稳定性。在随后的过程中,射流被不断拉伸,在起爆65μs后,尾翼边缘部分与射流分离。在起爆 96μs后,射流到达靶板位置,尾翼边缘部分出现第二个裂纹。射流的初始速度为1702m/s,着靶速度为1695m/s,这说明射流头部速度在飞行中基本保持不变。

图2 大锥角聚能射流形成过程

图3 给出了射流侵彻靶板过程,从图3中可以看出,在起爆96μs后,射流开始侵彻靶板,此时射流头部速度为1695m/s。射流头部与靶板高速撞击,并在其周围迅速形成塑性变形区和高温高压区,在靶板内产生较强的冲击波。在起爆111μs后,射流头部面积较小,在靶板表面开出一个小坑。在起爆116μs后,射流继续侵彻,头部受到高温高压和磨蚀的共同作用,因此,射流质量在不断减少,动能降低,射流头部也发生了较大的塑性变形,其横截面积增大,使侵彻靶板的直径增大。在起爆143μs后,射流的尾翼开始撞击靶板,而此时射流的速度也下降非常快,其动能也以较快的速度下降,在起爆150μs后,射流头部被严重破坏,射流出现很大的颈缩现象。最后,射流发生严重塑性变形,尾翼也断裂得非常严重,射流头部速度只有520m/s,已经不能再侵彻靶板。图4和图5分别给出了射流的平均速度和动能的变化关系。从这两个图中可以清楚地看出射流的形成和侵彻过程中平均速度和动能的变化。

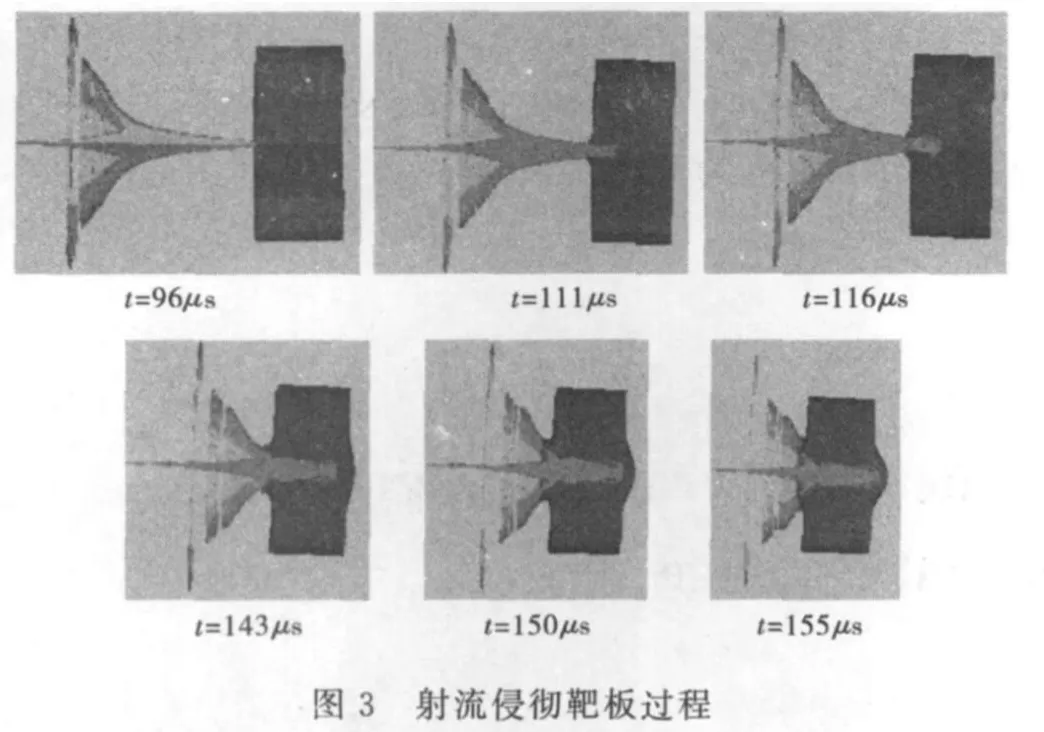
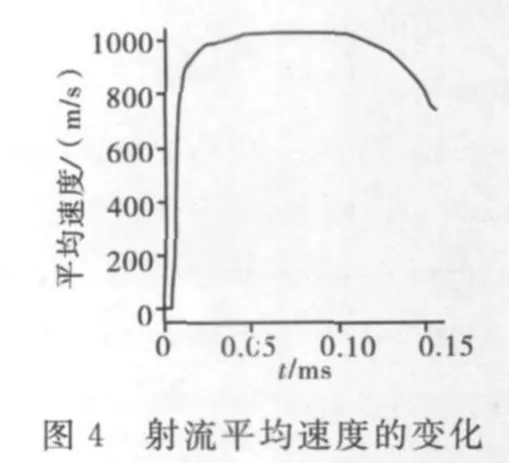
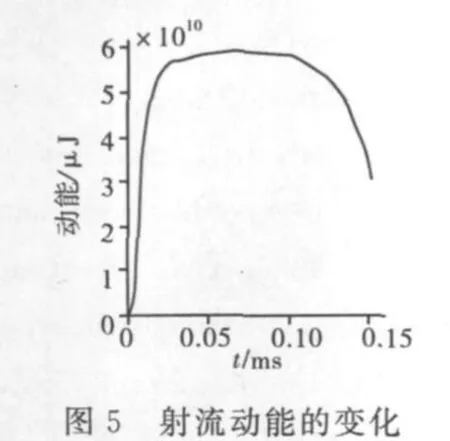
3 数值模拟与实验结果的对比分析

大锥角聚能装药射流的形成与侵彻的模拟结果与实验结果对比情况如表2所示。射流初始速度、着靶速度与实验结果误差分别为3.1%和2.8%,均小于5%。入孔孔径和穿深与实验结果相当,图6给出了侵彻靶板效果图,由对比结果来看,入孔形状基本相似。数值模拟结果与实验结果的对比表明,采用的数值模拟方法正确,分析合理。

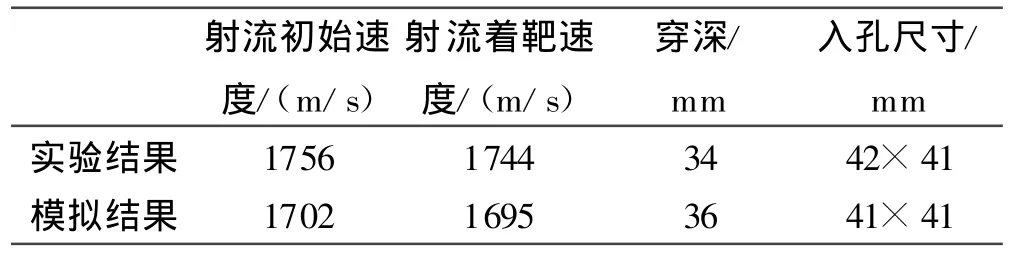
表2 结果对比情况表

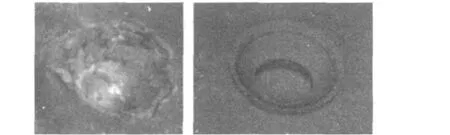
图6 侵彻靶板效果图

4 结论

1)采用Euler多物质与 Lagrange相结合的计算方法,可以模拟大锥角聚能装药射流的形成和侵彻钢靶过程,数值模拟结果与实验结果相吻合,说明该计算方法是正确的;

2)大锥角聚能射流是通过药型罩向后翻转而形成的,形状为漏斗型的聚能射流,具有良好的飞行稳定性和密实性;

3)射流在飞行过程中,其平均速度基本不变,当撞击靶板后,其速度和动能都快速衰减,直到不能再侵彻靶板为止;

4)在战斗部设计中,要充分考虑大锥角聚能装药的一些特性,合理设计出性能优良的战斗部。在防护设计中,要考虑大锥角聚能射流是漏斗型密实性射流,对付大锥角聚能射流就不能像设计对付小锥角射流那样去考虑,而是要像对付杆式侵彻体一样去考虑。

[1] Murphy M J,Kuklo R M.Fundamentals of shaped charge penetration in concrete,UCRL-JC-133126[R].1999.

[2] Christianson K L,Roth J R.Development of an enhanced warhead for the penetration augmented munition[C]//Proceedings of the 41st annual bomb&warhead technical meeting.San Diego,CA:Naval ocean systems center,1991.

[3] Mattsson K,Church J.Development of the K-charge,a short L/D shaped charge[C]//18th International Symposium on Ballistic,Lancaster,Pennsylvania:Technomic Publishing Company,Inc.,1999:528-534.

[4] 谭多望,孙承纬,赵继波,等.大锥角聚能射流实验研究[J].高压物理学报,2003,17(3):204-208.

[5] 谭多望,孙承纬.大锥角罩聚能装药射流理论计算方法[J].高压物理学报,2006,20(3):270-276.

[6] 王成,恽寿榕,黄风雷.大锥角聚能装药射流形成及对多层靶侵彻的数值模拟研究[J].爆炸与冲击,2003,23(4):349-354.

[7] 黄风雷,张雷雷,段卓平.大锥角药型罩聚能装药侵彻混凝土实验研究[J].弹箭与制导学报,2008,28(1):17-22.

[8] 张雷雷,朱鸿瑞,黄风雷.大锥角药型罩聚能装药结构对混凝土介质侵彻研究[J].弹箭与制导学报,2007,27(3):134-136.

[9] AUTODYN,Theory manual,Revision 4.0[Z].Century dynamics Inc.,1998.

[10] 廖海平,黄正祥,张先锋,等.亚半球罩聚能装药的杆式射流特性研究[J].弹箭与制导学报,2008,28(6):91-94.