低附带陶瓷球形破片衰减规律研究*
2011-12-07黄德雨张云逸王坚茹王绍志
黄德雨,张云逸,王坚茹,王绍志
(1中北大学机电工程学院,太原 030051;2轻武器论证研究所,北京 102202)
0 引言
冷战结束后,局部战争和地区冲突持续不断,城区作战的不断增加,作战模式发生了重大变化。在此背景下,减少对无辜人员的伤害已成为国际社会关注的一个问题。在已经结束的伊拉克战争中,根据统计,从2003年3月战争爆发截止到2008年1月,战争已造成伊拉克15.1万平民死亡,其中有相当一部分人是被装有大量预置破片的高威力战斗部爆炸后伤及无辜。这些预置破片往往是高密度的重金属材料,在爆轰驱动下,其初速和动能高,杀伤半径很大。如果采用低附带毁伤弹药,就可以做到定点清除,最大限度的避免平民伤亡,对敌人予以“点杀”。
经过试验研究发现,球形陶瓷破片由于密度低、衰减系数大、近距离杀伤能力强,远距离则只对人员造成巨大的心理恐惧与生理威慑作用。采用低密度的球形陶瓷作为战斗部预置破片,可以有效实现低附带毁伤的战技要求。
当战斗部完成设计、进行威力评估时,破片能否有效的杀伤目标与破片打击目标时的速度、形状和质量密切相关。因此,破片飞行规律成为研究的重要问题。国内外大多数破片飞行规律研究都是针对高初速钢质破片短距离飞行的,而对低密度破片以及长距离飞行的情况研究较少[1],为掌握陶瓷球飞行规律,为战斗部设计和威力评估提供依据,文中通过100m弹道靶实验,进行了陶瓷球长距离飞行时的空气阻力系数研究,得到了其飞行规律,利用此规律编制的程序来计算破片衰减速度,跟实际非常相符。
1 破片在空气中的运动[2]
破片在空气中的运动实际上是外弹道学问题。破片在空气中运动将受空气阻力和重力作用。由于破片从形成到击中目标所经过的时间一般不大,故可以不考虑重力的影响。即认为破片的飞行弹道为一直线,作用在破片上的外力只有空气阻力,这样,破片在空气中的运动方程可写为[3]:


式中:m为破片质量;v为破片速度;t为时间;C D为空气阻力系数;ρ为当地空气密度为破片迎风面积;R为破片据炸点飞行距离;v R为破片在R处的飞行速度;a称为破片衰减系数,是表征破片在飞行过程中保存速度能力的参数。在破片形状一定时,由空气动力学可知,C D与破片速度有关,表1[4]是球形破片阻力系数在不同马赫数下的值。

表1 球形破片阻力系数
2 计算方法
2.1 传统方法
用于低附带毁伤战斗部预置破片的陶瓷球密度低,有效杀伤半径小,在此距离以外速度衰减很快。传统确定破片衰减速度的方法是在破片测速试验的基础上计算出破片平均初速来代替破片初速,再根据破片初速选取衰减系数和飞行距离计算衰减速度。这种方法不符合破片低速长距离分行的实际情况,笔者将采用新的方法,对球形破片衰减速度分布规律进行研究。
工程上计算破片衰减速度,基本都是取空气阻力系数为常数[5],这在普通战斗部预置破片设计关心的范围内(约4~6Ma)高初速、短距离条件下是可行的。但是如果在低初速、远距离条件下也以空气阻力系数为定值来计算衰减速度,则可能出现错误的结果。以相同规格,不同初速的两个陶瓷球为例计算衰减速度,结果如表2所示。
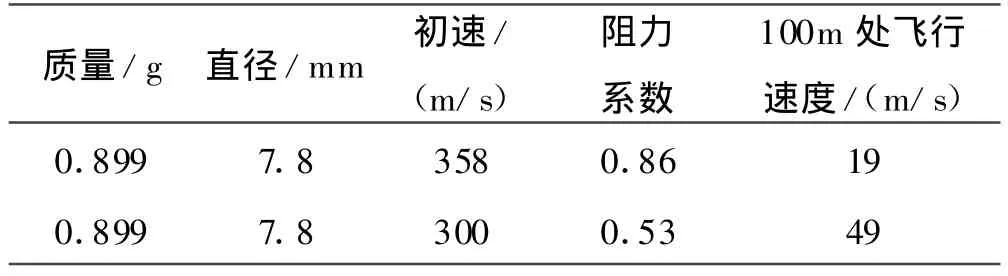
表2 定阻力系数法计算的衰减速度
由表2可看出在其他参数均相同的条件下,陶瓷球飞行到100m处时,初速高的陶瓷球速度竟然小于初速低的陶瓷球速度,这显然是不符合规律的。因此,计算球形破片的衰减速度时,在低初速、远距离条件下不能取空气阻力系数为定值。
2.2 变空气阻力系数法
下面采取一种新的计算方法来求远距离处(100m左右)破片的衰减速度。由式(2)可推导出破片飞行距离:

根据测出来的初速,参照表1选取相应的空气阻力系数(衰减系数随之确定),当破片速度衰减至下一速度区间的临界速度时(取此速度为衰减速度),将这两个速度代入式(4),则可确定此阶段的飞行距离;待速度衰减至下一区间时。重新选取相应的初末速度和衰减系数,即可求出相应飞行距离;依此类推,可求出破片飞行至预定距离处的衰减速度。
以小球初速v0=200m/s,m=0.899g,φ=7.8mm,以求其飞行至100m处衰减速度为例,计算步骤如下:
1)马赫数Ma=200/340=0.59,介于0.4和0.6之间,查表 1该区间阻力系数C D=0.51,v1=340*0.4=136m/s,将以上参数代入式(3),得飞行距离R1=22m;
2)此处破片速度为v 1=136m/s,C D=0.48,v2=340*0.2=68m/s,将此参数代入式(3),得飞行距离R2=42m;
3)此处破片速度为v2=68m/s,C D=0.47,R=100-R1-R2=36m,将此参数代入式(1),得100m处衰减速度v3=38m/s。
利用此方法可以很容易的利用C++软件编写预置破片在空气中的飞行速度衰减规律程序。下面利用此方法编制的程序计算破片衰减速度,与试验做验证对比。
3 试验与结果分析
3.1 试验
为掌握陶瓷球长距离飞行时的速度衰减规律,在枪口处采用测速网靶[1]对陶瓷球的初速进行了测量,在穿过测速网靶时弹托和陶瓷球分离,以保证发射系统不影响实验。由于网靶中心距离枪口很近,可以近似认为测试的速度就是枪口初速。图1是试验用的陶瓷球及其装配情况。
试验在100 m弹道靶上进行。该弹道靶主要由发射器(7.62 mm滑膛枪)、测速靶和目标靶组成,总长100 m,测速网靶放置于枪口,目标靶置于靶道末端100m处。由于陶瓷球质量较轻,在发射出去后容易受到干扰而产生偏移,在100m终点处难以测量其衰减速度,因此目标靶为一层1m2(120g/m2)的牛皮纸,穿透该纸所需比动能约为3.5J/cm2。在程序中输入陶瓷球尺寸参数、初始速度和飞行距离,可以得到飞行距离处的衰减速度、动能和比动能。为了对比结果的准确性,对6发参数不同的陶瓷球进行了试验,程序计算数据和陶瓷球打到纸上的状态进行对比的结果如表3所示。

图1 试验用的陶瓷球破片

表3 试验与计算结果对比
3.2 结果分析
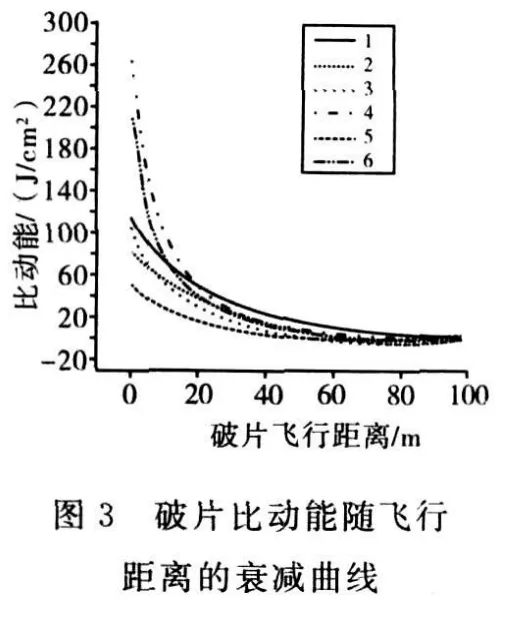
根据表3的统计数据,还可以通过程序绘出速度和比动能随飞行距离的衰减曲线(图2、图3)。由图上的曲线可看出,采用2.2的方法计算球形破片在100m处的速度与实验结果基本相符,这证明计算方法理论可行。同时也可得出几点结论:
1)在飞行较远距离时,球形破片的质量对速度衰减程度影响很大。
2)在一定的飞行距离内,初速越大,速度衰减越快;而飞行到较远距离时,速度已经相差不多了。
3)破片在质量较小而初速较大的情况下,其比动能衰减很快(如图3中的4号曲线),低附带毁伤特性越明显。

4 结束语
通过试验研究不同尺寸的低密度陶瓷材料球形破片在低初速条件下长距离飞行时的速度衰减规律,结果表明,球形破片在低初速长距离飞行时其空气阻力系数CD与飞行马赫数有关,因此其衰减系数a不是常数。在低附带毁伤战斗部设计关心的杀伤范围外(5~100m),应根据破片飞行过程中经历的不同速度阶段选取相应的阻力系数来计算破片衰减速度。
[1] Brinkley R F.Ballistics of Projectile Fragments[M].Pennsylvania:Bureau of Mine,1968:73-78.
[2] [美]陆军装备部.终点弹道学原理[M].王维和,李惠昌,译.北京:国防工业出版社,1988:246-251.
[3] 翁佩英,任国民,于骐.弹药靶场试验[M].北京:兵器工业出版社,1995:94-100.
[4] 马永忠,李其祥,杨光.对弹丸破片速度衰减规律的探讨[J].弹箭与制导学报,2000,20(3):59-64.
[5] 谭多望,王广军,龚晏青,等.球形钨合金破片空气阻力系数实验研究[J].高压物理学报,2007,21(3):231-236.
