夹层旋转扁壳轴对称非线性稳定的样条函数解法

侯朝胜

(天津大学建筑工程学院，天津 300072)

夹层板壳因重量轻、刚度大等优良特性在航空、航天、航海和海洋工程得到广泛应用．在进行非线性的计算时，由于数学上的困难，一般都采用Reissner模型．刘人怀[1]首先建立夹层圆板非线性弯曲方程，他同其他作者进一步推广到夹层扁球壳[2-6]和夹层扁圆锥壳[7-8]．本文把文献[9]的公式和方法推广，计算夹层旋转扁壳的非线性稳定，而把球壳或圆锥壳作为其特例．

1 基本方程及边界条件

设夹层旋转扁薄壳的中面方程为

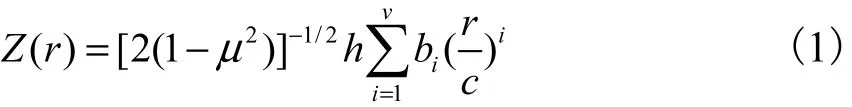
式中：Z为中面竖向坐标；r为径向坐标；μ为表板泊松比；h为壳厚度；b i为无量纲常数；c为壳底面圆半径．设夹层扁壳受分布荷载(r)或均布边缘力矩作用，采用文献[9]的Reissner 模型、符号和无量纲量，再引入

旋转夹层扁壳的无量纲非线性弯曲方程式及转角[2-3,8-9]为

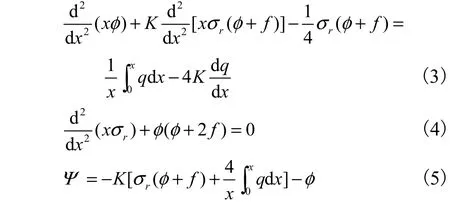
不考虑边缘的径向力和预应力，问题的边界条件[9]为

2 问题求解

选3 次B 样条函数为试函数，分划x 定义域为n等分，分点号依次为0，1，…，n．虚设2 个结点为－1 和n＋1，取s＝1/n，xi＝i/n，设

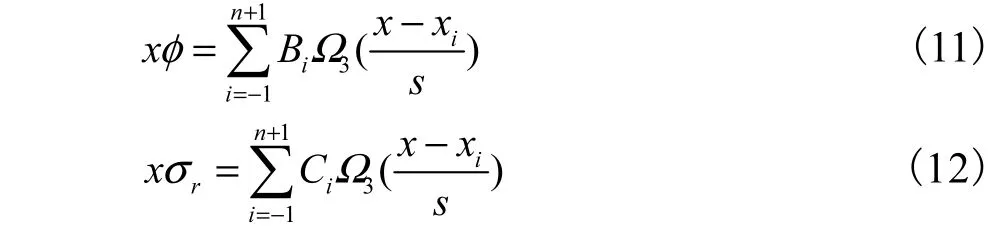
采用同文献[9]一样的推导过程，把式(11)和式(12)代入式(3)和式(4)，对第i个结点可得

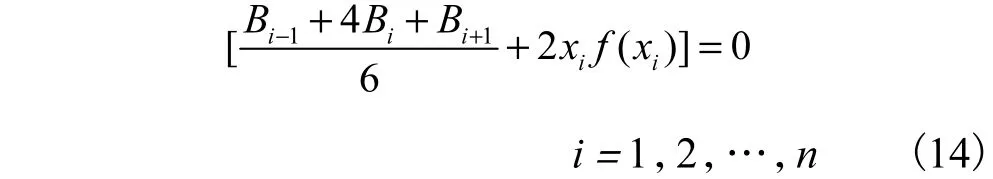
对i＝0 结点，若忽略中心的奇异性得，即

对边界条件式(6)～式(9)进行推导可得

式(13)～式(20)共2n＋6 个非线性方程，用牛顿迭代法求解可以确定2n＋6 个待定系数Bi、Ci(i＝－1，0，1，…，n，n＋1)．进一步可得内力及挠度．挠度表达式为

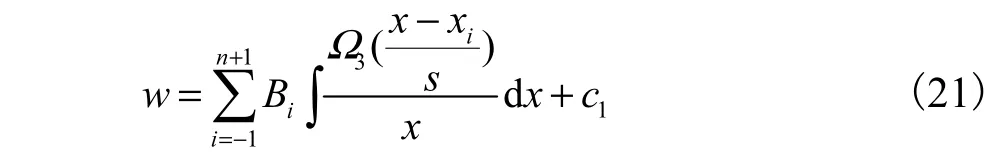
式中积分常数c1由边界条件式(10)确定．

解非线性方程的方法和收敛精度见文献[9]．

用试算法计算扁壳的稳定性，采用抛物线法[6]或逐步加(减)载法[10]确定上、下临界荷载．

3 算例及说明

所有算例中，表板泊松比μ＝0.3．表中点数n即为式(11)～式(21)的n．表中的数据均为无量纲．表1～表3 中3 种壳的中面坐标参数如下．

表1 受均布荷载作用的夹层壳的临界荷载(K＝0.05)Tab.1 Critical loads of sandwich shells subjected to uniformly distributed load (K＝0.05)

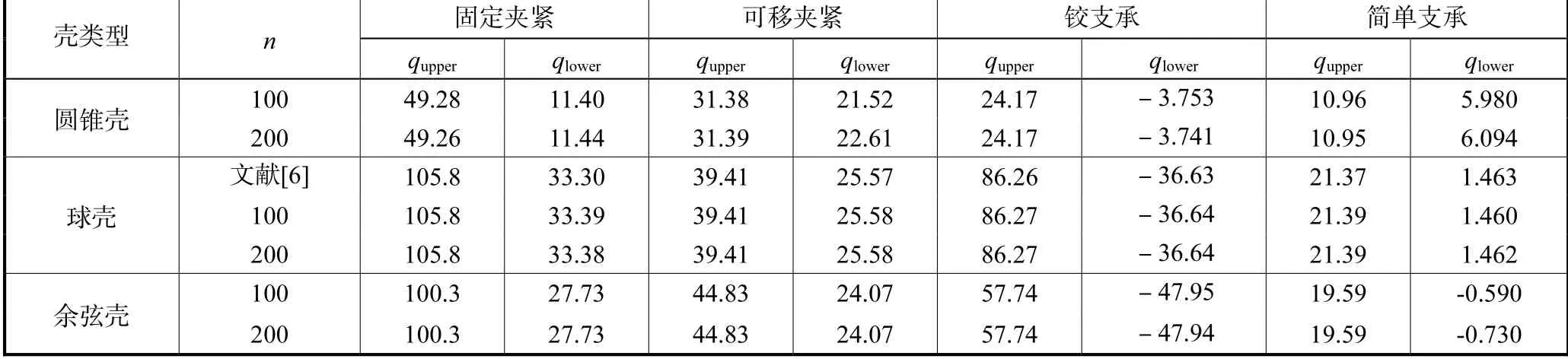
表2 受均布荷载作用的夹层壳的临界荷载(K＝0.01)Tab.2 Critical loads of sandwich shells subjected to uniformly distributed load (K＝0.01)

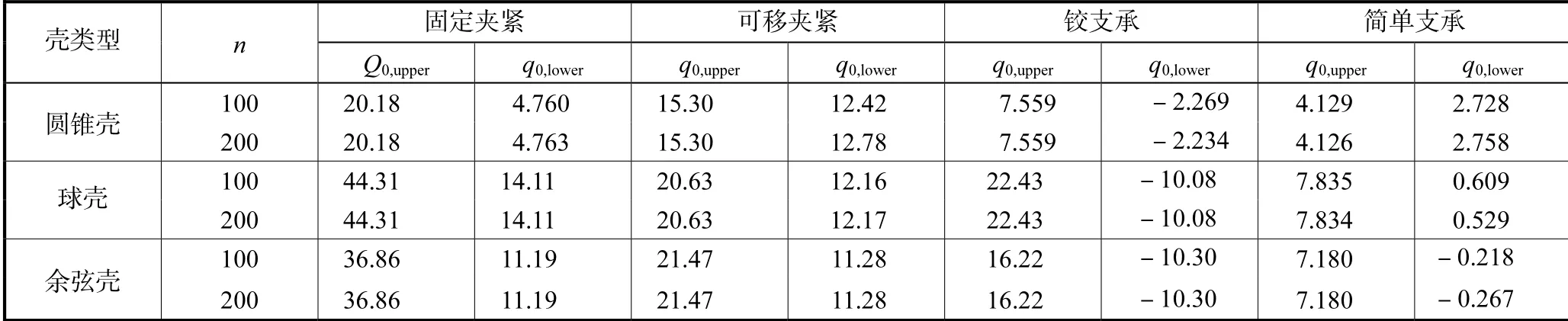
表3 受9次多项式分布荷载作用的夹层壳的上、下临界荷载(K＝0.01)Tab.3 Critical loads of sandwich shells subjected to 9-degree polynomial distributed loads (K＝0.01)

(1) 圆锥壳：v＝1，b1＝10．

(2) 球壳：v＝2，b1＝0，b2＝10．

在表4～表6 中，文献[2，4，8]的数据是按图估计，然后换算得出的．文献[6]的数据是用幂函数法得出的．

表4 受均布边缘力矩的简支夹层球壳的临界荷载Tab.4 Critical loads of spherical sandwich shells with simply supported edge subjected to uniform edge moments

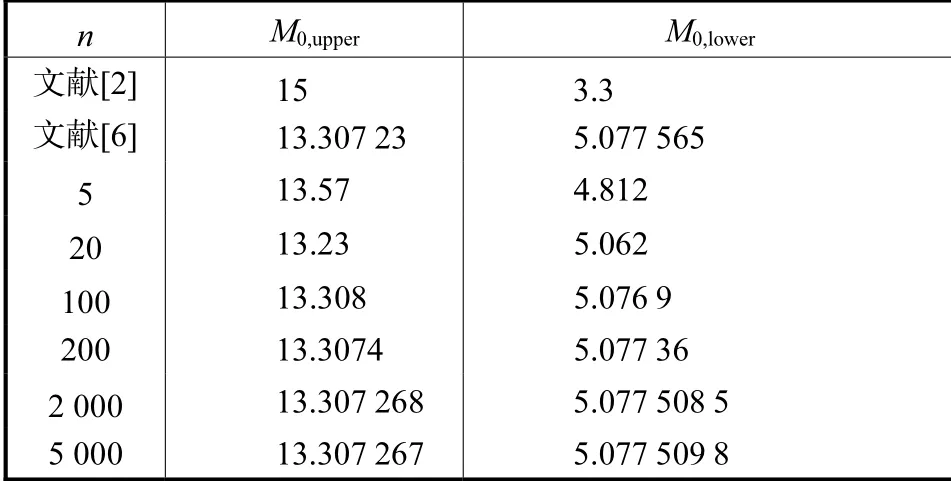
表4 受均布边缘力矩的简支夹层球壳的临界荷载Tab.4 Critical loads of spherical sandwich shells with simply supported edge subjected to uniform edge moments

n M0,upper M0,lower文献[2] 15 3.3文献[6] 13.307,23 5.077,565 5 13.57 4.812 20 13.23 5.062 100 13.308 5.076,9 200 13.3074 5.077,36 2 000 13.307,268 5.077,508,5 5 000 13.307,267 5.077,509,8

表5 受均布荷载作用的夹层扁球壳的上、下临界荷载及中心挠度(K＝0.05)Tab.5 Upper，lower critical loads and central deflection of shallow spherical sandwich shells subjected to uniformly distributed load (K＝0.05)

表6 固定夹紧夹层扁圆锥壳受均布荷载的临界荷载(K＝0.05)Tab.6 Critical loads of shallow conical sandwich shells with rigidly clamped edge subjected to uniformly distributed loads(K＝0.05)

4 结 论

(1)本文导出了计算夹层旋转扁壳的大挠度公式的一般形式．本文的解与幂函数法的解[3，6]非常一致，说明本文提出的方法是可靠的、有效的．与摄动解差别较大是因为摄动解[2，4，8]是低阶解，精度较低．

(2)一般地说，如浮点数的有效数字足够长，只要点数增加，可得到更高精度的解答．用不同的点数计算同一问题，比较它们的结果可判断解的精度和收敛范围．

(3)计算球壳的精度高于计算圆锥壳的精度．因计算下临界荷载时，壳处于大变形状态，故一般情形下，计算下临界荷载的精度低于计算上临界荷载的精度．

(4)对比表1 和表2，可见剪切参数K对计算结果有较大的影响．不论支承条件，3 种壳(圆锥壳、球壳、余弦壳)的上临界荷载及上、下临界荷载的差值随K值的减小而增大．

(5)使用幂函数法，结果表明剪切参数K对收敛范围的影响大．若K增加一点，收敛的荷载范围迅速减小，对简单支承影响更大(见文献[6]结论5)．使用本文的方法可解决这一问题．也就是说当剪切参数K增加，使收敛的荷载范围减小时，在较大荷载范围内，用本文的方法仍能得到收敛的解．这表明了幂函数解的收敛范围远小于样条函数解的收敛范围．

(6)整个程序用Fortran 语言写成，计算时仅需输入中面坐标形状参数、剪切参数、泊松比、支承条件、点数、荷载、计算临界荷载的方法(逐步加载法、抛物线法等)及第1 个荷载的初值，就可求出临界荷载．

(7)据笔者所知通用的有限元程序 ANSYS、ABAQUS 等均没有Reissner 模型．本文的结果可为开发此类问题的计算程序提供参考解答．本文方法比有限元法的计算时间少．

［1］Liu Renhuai. Nonlinear bending of circular sandwich plates[J].Applied Mathematics and Mechanics，1981，2(2)：189-208.

［2］Liu Renhuai，Cheng Zhenqiang. On the nonlinear buckling of circular shallow spherical sandwich shells under the action of uniform edge moments[J].Int J Non-Linear Mech，1995，30(1)：33-43.

［3］侯朝胜，李忠献. 夹层扁薄球壳的非线性稳定[J]. 天津大学学报，1997，30(4)：495-499.Hou Chaosheng，Li Zhongxian. Nonlinear stability of a shallow spherical thin shell of sandwich construction[J].Journal of Tianjin University， 1997 ， 30(4)： 495-499(in Chinese).

［4］徐加初，王 乘，黄玉盈，等. 夹层扁球壳的非线性稳定性[J]. 固体力学学报，2000，21(4)：366-370.Xu Jiachu ， Wang Cheng ， Huang Yuying ， et al.Nonlinear stability of shallow spherical sandwich shells[J].ACTA Mechanica Solida Sinica，2000，21(4)：366-370(in Chinese).

［5］侯朝胜，周伟毅. 轴对称线布荷载作用下夹层圆板和夹层球壳的非线性弯曲[J]. 天津大学学报，2009，42(3)：227-230.Hou Chaosheng，Zhou Weiyi. Nonlinear bending of circular sandwich plates and shallow spherical sandwich shells subjected to axisymmetric line load[J].Journal of Tianjin University， 2009 ， 42(3)： 227-230(in Chinese).

［6］侯朝胜，周伟毅. 夹层圆板和夹层扁球壳非线性弯曲的进一步研究[J]. 天津大学学报，2009，42(12)：1072-1077.Hou Chaosheng，Zhou Weiyi. Further study on nonlinear bending of circular sandwich plates and shallow spherical sandwich shells[J].Journal of Tianjin University，2009，42(12)：1072-1077(in Chinese).

［7］Liu Renhuai，Li Jun. Nonlinear vibration of shallow conical sandwich shell[J].Int J Non-Linear Mech，1995，30(2)：97-109.

［8］Liu Renhuai，Li Jun. Nonlinear stability of shallow sandwich conical shell[J].Applied Mechanics and Engineering，2000，5(2)：367-387.

［9］侯朝胜，张守恺，林 锋. 夹层圆板非线性弯曲和屈曲的样条函数解法[J]. 应用数学和力学，2005，26(1)：120-126．Hou Chaosheng，Zhang Shoukai，Lin Feng. Cubic spline solutions of axisymmetrical nonlinear bending and buckling of circular sandwich plates[J].Applied Mathematics and Mechanics， 2005 ， 26(1)： 120-126(in Chinese).

［10］侯朝胜. 用矩法计算受轴对称分布荷载的扁圆壳薄壳的非线性稳定[J]. 工程力学，1987，4(1)：1-10.Hou Chaosheng. Nonlinear stability of conical shallow shells subjected to axisymmetric distributed load by using the moments method[J].Engineering Mechanics，1987，4(1)：1-10(in Chinese).