基于可能度的区间数排序方法比较

肖 峻，张 跃，付 川

(天津大学智能电网教育部重点实验室，天津 300072)

多属性决策(multi-attribute decision making ，MADM)，也称为有限方案多目标决策，普遍存在于企业生产规划、工程建设项目优选、企业效益评估等实际问题中，它是决策理论与方法研究的一个重要内容．目前，由于客观事物的复杂性和不确定性，以及人类思维的模糊性，对于不确定多属性决策问题的研究，已经引起了广泛重视[1-6]．从目前已有关于不确定多属性问题的研究成果来看，大多限于研究如何计算各决策方案的综合评价值，即主要侧重于权重和模型的研究和综合求解，而对以区间数表示的方案评价值如何进行方案排序的研究较少．通常，由于区间数之间可能存在相互交叉部分，所以直接进行方案的排序是困难的．目前普遍采用的排序方法是文献[7]中所述的基于可能度的排序法，同时文献[8]也给出了另一种关于可能度的区间数排序的方法，但未给出可能度定义的详细解释．

本文通过实例计算分析比较了这2 种可能度算法，并对可能度的含义给出了理论解释．

1 不确定多属性决策中的区间数排序

定义1[8]设R 为实数域，称闭区间[xL，xU]为区间数，其中xL，xU∈R，xL＜xU．

设S＝{s1，s2，…，sn}为方案集，Q＝{Q1，Q2，…，Qm}为属性集，w＝{w1，w2，…，wm}为属性的权重向量．对于方案sj∈S，按第i个属性Qi进行测度，得到sj关于Qi的属性值为区间数aij，这里aij＝[aijL，aijU]，从而构成决策矩阵A＝(aij)m×n．

得到决策矩阵A并利用文献[9]所述方法可以求出各方案所对应的综合属性值z1，z2，…，zn．zj(j＝1，2，…，n)表示综合各因素后的第j个方案的相对优越性评价值．它是决策者从集合S中选择一个最好方案所凭借的主要依据．

由于这些评价值均是区间数的形式，即zj＝[zjL，zjU]，并且可能存在2 个区间数综合属性值相互交叉的情况，所以，根据评价值z1，z2，…，zn直接进行所有方案的排序是比较困难的，需要对区间数进行排序，才能够确定最优方案．可见，为了最终得到各方案的排序关系，对各方案的综合属性值区间进行排序是一个致关重要的环节．

目前，通常采用基于可能度计算的排序方法对各方案的综合属性值区间进行排序．首先研究2 个区间数之间的比较，下面的定义2 介绍了可能度的概念．

定义2设区间数a＝[aL，aU]和b＝[bL，bU]，记p(a≥b)为a≥b的可能度，其数值大小根据不同的可能度定义公式来确定．

可能度的取值一般在0～1 之间，用来衡量2 个区间数之间的大小关系．知道了2 个区间数的大小评判方法，若在n个区间数zj＝[zjL，zjU](j＝1，2，…，n)之间两两进行比较，将其比较可能度值建立的n×n的矩阵称为可能度矩阵P＝(pij)n×n，其中pij＝p(zi≥zj)．

建立P后，为对n个区间数排序，文献[10]给出的可能度矩阵排序公式为

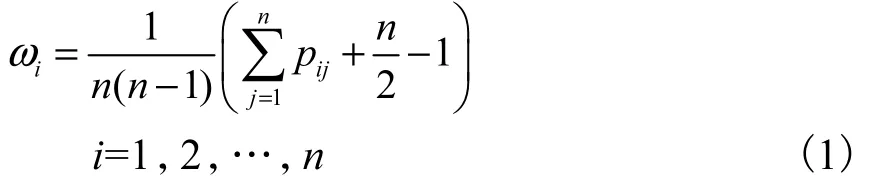
通过式(1)对可能度矩阵P进行排序计算可以得到排序向量ω＝(ω1，ω2，…，ωn)T，并按其分量大小对方案进行排序，就可以确定最优方案．可见，对区间数的排序实质是将区间数的大小关系转化为可能度排序向量的大小关系，从而找到最优方案．

2 区间数排序可能度的2种定义

2.1 文献[7]中可能度的定义

定义3[7]设a＝[aL，aU]和b＝[bL，bU]，且记L(a)＝aU－aL，L(b)＝bU－bL，则称

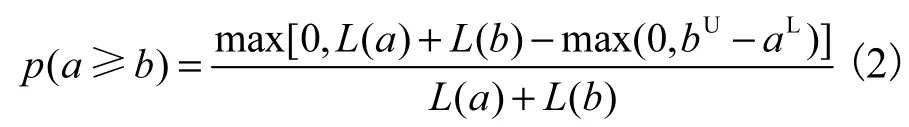
为a≥b的可能度．

由以上定义可以看出，可能度的取值在0～1 之间，并具有如下的性质：

(1)若p(a≥b)＝p(b≥a)，则p(a≥b)＝p(b≥a)＝1/2；

(2)p(a≥b)＋p(b≥a)＝1；

(3)若aU≤bL，则p(a≥b)＝0，若bU≤aL则p(a≥b)＝1；

(4)对于3 个区间数a、b、c，若a≥b，则p(a≥c)＝p(b≥c).

2.2 文献[8]中可能度的定义

除了以上的可能度定义外，文献[8]也给出了关于可能度计算的另一种定义．该定义由以下2部分组成．

相应的b＞a的可能度计算式为

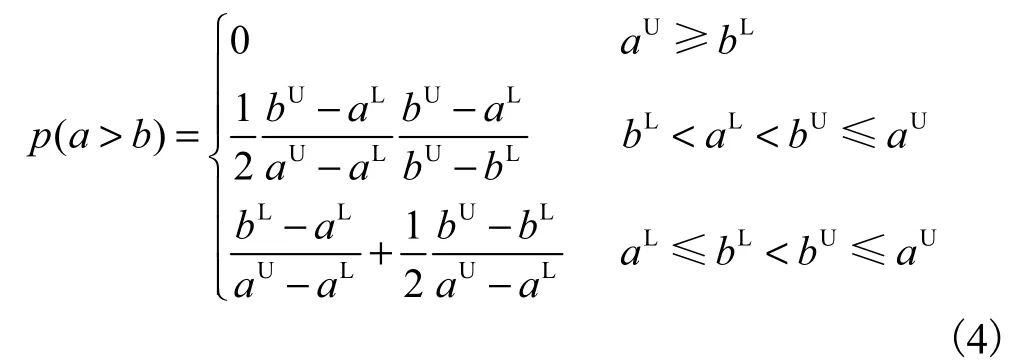
为了便于研究和计算，本文将这2 个公式合并为如下定义．

定义4设a＝[aL，aU]和b＝[bL，bU]，记L(a)＝aU-aL，L(b)＝bU-bL，则a≥b的可能度p(a≥b)为

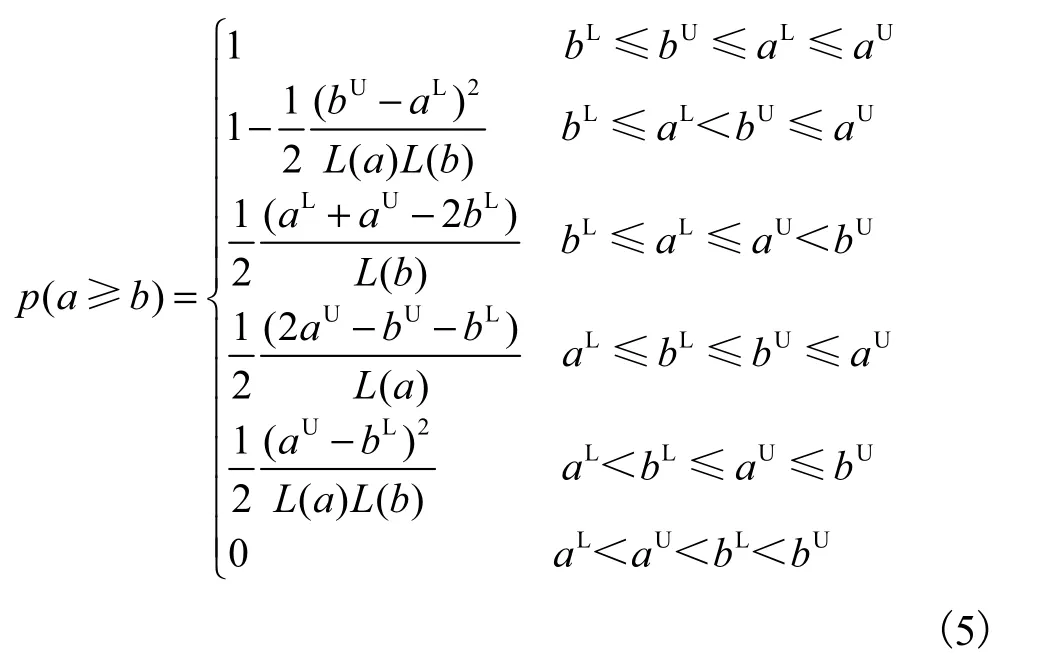
文献[8]以式(3)和式(4)的形式给出可能度定义，但没有详细的推导过程．为对这2 种可能度的定义方式进行比较，以下对可能度的含义进行理论剖析．

2.3 区间数排序可能度的含义

由于a＝[aL，aU]和b＝[bL，bU]中，a和b中的取值分别是服从均匀分布的，而且显然它们的取值情况是相互独立的，因此可把区间a和b的可能度关系问题转化为以下问题．

从区间[aL，aU]和[bL，bU]内随机取值u和v，求u大于v的概率，即p(a≥b)．

由于u和v相互独立，且分别服从均匀分布，则二维随机变量(u，v)也服从均匀分布．二维随机变量(u，v)的联合概率密度函数f(u，v)为

设横坐标表示u点的取值情况，纵坐标表示v点的取值情况．根据u和v取值区间边界点的相互关系以及边界区域与直线y＝x的位置关系，可以将u和v的概率密度f(u，v)分布分为6 种情况，并做出f(u，v)的分布图，见图1．

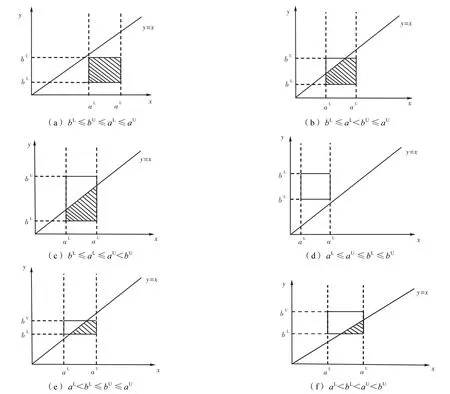
图1 概率密度f(u，v)分布Fig.1 Profile of probability density function f(u，v)

为了便于分析，将区间[aL，aU]和[bL，bU]所围的矩形区域被直线y＝x所截的下侧画为阴影部分．根据概率理论知识，由于二维随机变量(u，v)服从均匀分布，那么概率p(a≥b)为图中阴影面积与矩形面积之比．当然概率p(a≥b)也可以根据概率密度函数式(6)通过积分求得，即

式中D为图1 中阴影部分区域．

以下对图1 中的6 种情况分别进行讨论，并求出每种情况对应的可能度计算式．

1)bL≤aL(记L(a)＝aU－aL，L(b)＝bU－bL）

(1)若bU≤aL，f(u，v)分布见图1(a)．显然，a大于b的概率为1，即p(a≥b)＝1．

(2)若aL＜bU≤aU，f(u，v)分布见图1(b)．p(a≥b)计算结果为

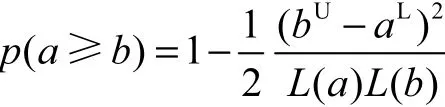
(3)若bU＞aU，f(u，v)分布见图1(c)．p(a≥b)计算结果为

2)bL＞aL

(1)若aU≤bL，f(u，v)分布见图1(d)．由于阴影面积为0，显然概率p(a≥b)＝0．

(2)若bU≤aU，f(u，v)分布见图1(e)．p(a≥b)计算结果为

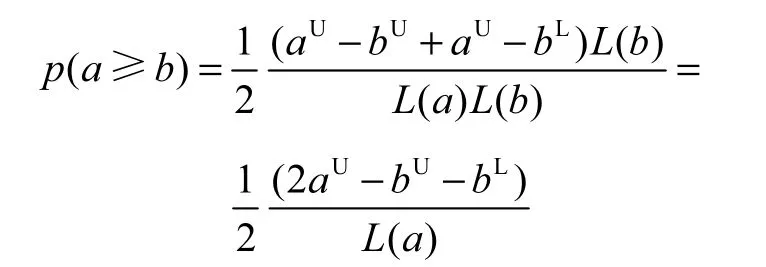
(3)若bU＞aU＞bL，f(u，v)分布见图1(f)．p(a≥b)计算结果为

将以上6 种情况进行综合，就可得到定义4 中的可能度计算公式．

由于可能度定义3 和可能度定义4 的形式不同，因而按照这2 种方法计算得到的可能度矩阵和排序向量也不同．为了比较在这2种定义之间哪种方法得到的排序向量能够更好地反映各方案之间的优劣关系，能够使决策者更准确地找到最优方案，具有更高的有效性和优越性，有必要对可能度定义3 和定义4 做进一步的分析比较．

3 可能度定义的比较

3.1 算例分析

本文首先采用文献[9]的算例来比较这2 种可能度定义下的计算结果．

算例1[9]考虑一个市政图书馆的空调系统选择问题，有5 个备选方案xj(j＝1，2，3，4，5)，而评价方案的主要依据是3 个因素，即经济性、功能性和可操作性.这3 个因素又可划分为8 个属性，即固定成本(Q1)、管理成本(Q2)、性能(Q3)、噪音(Q4)、可维护性(Q5)、可靠性(Q6)、灵活性(Q7)和安全性(Q8)．其中，Q3、Q5、Q7和Q8的属性值为打分值，其范围为1(最差)～10 分(最好)之间．另外，Q1、Q2和Q4为成本型属性，其他5 个属性为效益型属性．该问题的决策矩阵A 和属性权重向量w 如表1 所示．

表1 决策矩阵A 和属性权重向量w(算例1)Tab.1 Decision matrix A and attribute weight vector w(case 1)

表2 2种可能度定义下的排序结果比较(算例1)Tab.2 Comparison of ranking results based on two different definitions(case 1)

从上面的例子可以看出，2 种可能度计算方法可以得到同样的排序结果，即s4＞s5＞s1＞s3＞s2．用可能度定义3 计算得到的排序向量间的差值较小．正因为这种排序向量差值的区别，可以推测在一定情况下有可能出现定义3 不能够精确地区分属性值区间，而出现某几个方案所对应的排序向量相同的情况．采用以下的算例对此假设进行证实．

算例2[3]考虑一个大学的学院评估问题．采用教学(Q1)、科研(Q2)和服务(Q3)这3 个属性作为评估指标，设有5 个学院(A，B，C，D，E)将被评估．为了便于分析和比较，本文改变了原算例决策矩阵A各元素区间值，保留了原文的权重区间，分别如表3和表4 所示．

与算例1 相同，用文献[9]中所述单目标最优化模型及相应的公式求出各方案综合属性值区间为

用可能度定义3 和定义4 分别对这5 个方案的综合属性值区间计算可能度矩阵，并计算排序向量，其结果见表5．

表3 属性权重w(算例2)Tab.3 Attribute weight w(case 2)

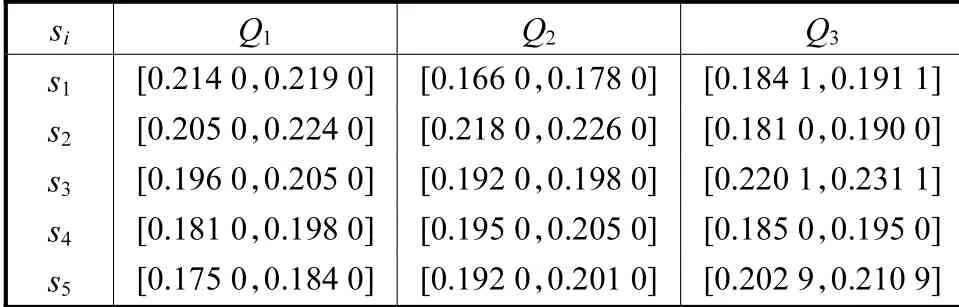
表4 决策矩阵A(算例2)Tab.4 Decision matrix A(case 2)

表5 2种可能度定义下的排序结果比较(算例2)Tab.5 Comparison of ranking results based on two different definitions(case 2)

从表5 看出，用定义3 计算可能度矩阵得到的排序向量ω2＝ω3，ω1＝ω4＝ω5，无法进行排序，而用可能度定义4 可判断出方案排序关系是s2＞s3＞s1＞s5＞s4．

由此可见，用可能度定义4 进行计算可增大排序向量间的差值，在一些情况下可以解决用定义3 无法进行排序的问题，因此可能度定义4 能够更准确地解决不确定多属性决策中的排序问题，具有一定的优越性．

3.2 数理分析

下面从数理角度分析2 种可能度定义的区别．为了分析方便，将定义3 的公式改写为

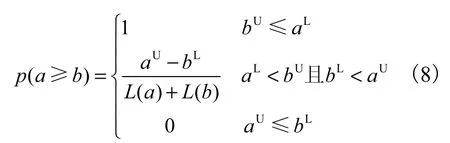
已知a＝[aL，aU]和b＝[bL，bU]，记L(a)＝aUaL，L(b)＝bU-bL，aφ=(aU+ aL)/ 2．假定b和L(a)不变，以aφ为变量，分析2 种定义下的可能度p(a≥b)的区别．

首先，将式(8)对aφ求导，得

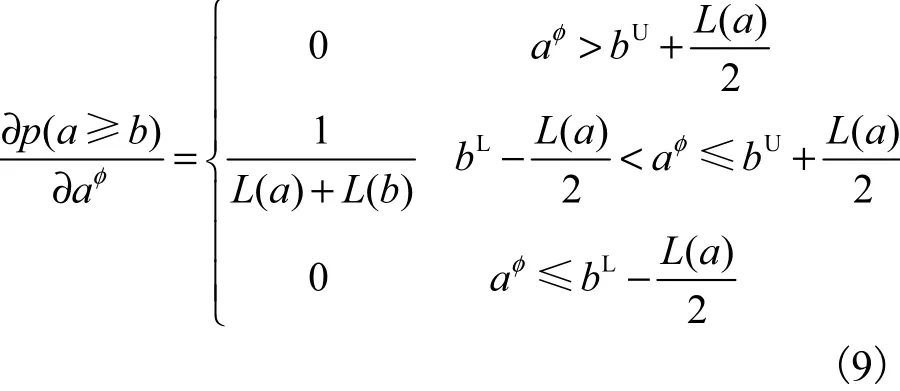
当 L(a) ＞ L(b)时，将式(5)对aφ求导，得

类似地，当L(a) ≤L(b)时，将式(5)对aφ求导，得

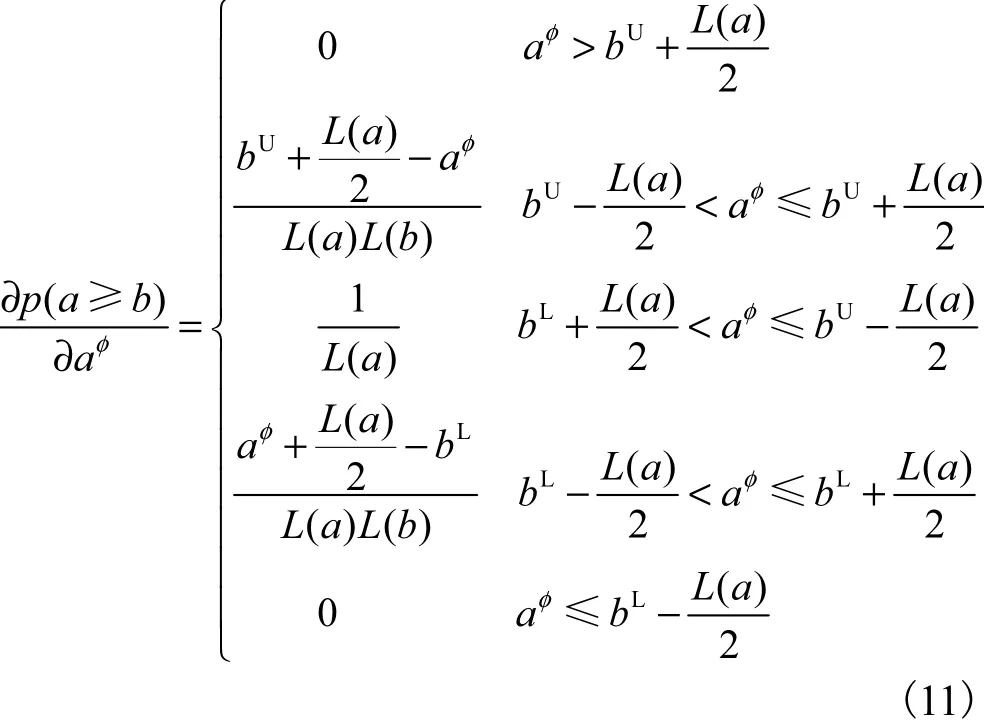
当L(a)＞ L(b)时，根据式(9)和式(10)，绘制定义3 和定义4 下可能度随aφ的变化情况，如图2 所示，L(a) ≤L(b)时的变化情况与此图类似，只是定义4下的中间直线线段的斜率不同．分析可得如下结论．

(1)2 种定义下的曲线均能表征p(a≥b)随aφ增加而变大的趋势，当L(a) ≤L(b)时的情况与此类似．

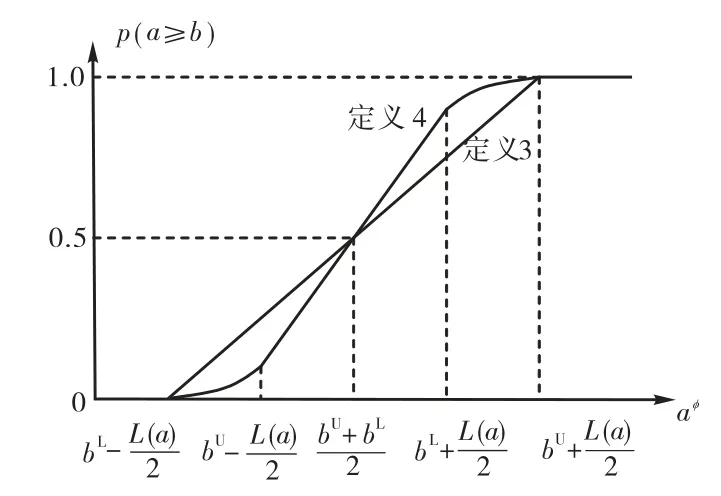
图2 p(a≥ b)随aφ 变化示意Fig.2 Change of p(a≥b)with aφ

因此相同情况下，定义4 下的p(a≥b)更加接近于0 或1，即更大程度地表征了a和b的差异．从表2 和表5 的可能度矩阵P可以看出这种现象．

从原理上讲，定义4 在区间取值均匀分布条件下进行概率分析得到可能度，准确体现了区间数的不确定性，在图形上表现为面积之间的比例．而定义3 则直接用一个区间数的上限值和另一个区间数的下限值的差，然后除以区间长度和得到可能度，在图形上表现为线段比，并没有考虑关于区间取值上如何分布的问题，一定程度上破坏了区间取值均匀分布的前提．

在应用上，定义4 中可能度能够准确表达区间数之间的大小关系，适用于区间数的精确比较．而定义3 是定义4 的一种线性化，有一定误差，尤其在区间数两者长度接近且重叠比例接近1/2 时，误差更大，应避免使用．但是，定义3 中可能度的表达式较为简单，适用于大量数据的快速计算．因此，在开发大规模计算算法时，可以结合2 种定义，预判断误差程度，合理选择计算公式．

4 结 语

对于决策方案的综合属性值以区间数形式表示的不确定多属性决策问题，本文就其中的综合属性值排序环节中的2 种可能度定义进行了分析比较，并对可能度的含义进行了剖析，同时从数理角度分析2 种可能度定义的区别．通过比较和分析可以看出，文献[8]中的可能度定义能够准确表达区间数之间的大小关系，适用于区间数的精确比较．由该可能度定义所得各方案的排序向量间的差值较大．基于这种可能度定义的决策方案排序方法可以避免采用文献[7]中可能度定义导致的各方案的综合属性值区间差别较小时而无法进行排序的问题．而文献[7]中可能度定义的表达式较为简单，便于大规模计算．因此，实际应用中可以根据具体情况合理选择，以同时满足精度和速度的要求．

［1］Yoon K. The propagation of errors in multiple-attribute decision analysis：A practical approach[J].Journal of the Operational Research Society，l989，40(7)：68l-686.

［2］Huynh V-N，Nakamori Y，Tu-Bao Ho，et al. Multipleattribute decision making under uncertainty：The evidential reasoning approach revisited[J].Systems，Man and Cybernetics(Part A)：Systems and Humans，IEEE Transactions，2006，36(4)：804-822.

［3］Bryson N，Mobolurin A. An action learning evaluation procedure for multiple criteria decision making problems[J].Eur J Oper Res，1996，96(3)：379-386.

［4］Xu D L，Yang J B，Wang Y M. The evidential reasoning approach for multi-attribute decision analysis under interval uncertainty[J].Eur J Oper Res， 2006 ，174(3)：1914-1943.

［5］Guo M，Yang J B，Chin K S，et al. Evidential reasoning based preference programming for multiple attribute decision analysis under uncertainty[J].Eur J Oper Res，2007，182(3)：1294-1312.

［6］Yang J B，Wang Y M，Xu D L，et al. The evidential reasoning approach for MADA under both probabilistic and fuzzy uncertainties[J].Eur J Oper Res，2006，171(1)：309-343.

［7］达庆利，刘新旺. 区间数线性规划及其满意解[J]. 系统工程理论与实践，1999，19(4)：3-7.Da Qingli，Liu Xinwang. Interval number linear programming and its satisfactory solution[J].Systems Engineering—Theory & Practice，1999，19(4)：3-7(in Chinese).

［8］张 全，樊治平，潘德惠. 不确定性多属性决策中区间数的一种排序方法[J]. 系统工程理论与实践，1999，19(5)：128-133.Zhang Quan，Fan Zhiping，Pan Dehui. A ranking approach for interval numbers in uncertain multiple attribute decision making problems[J].Systems Engineering—Theory & Practice，1999，19(5)：129-133(in Chinese).

［9］徐泽水，达庆利. 不确定多属性决策的单目标最优化模型[J]. 系统工程学报，2002，17(1)：50-54.Xu Zeshui，Da Qingli. Singule-objective optimization model in uncertain multi-attribute decision-making[J].Journal of Systems Engineering，2002，17(1)：50-54(in Chinese).

［10］樊治平，张 全. 一种不确定性多属性决策模型的改进[J]. 系统工程理论与实践，1999，19(12)：42-47.Fan Zhiping，Zhang Quan. The revision for the uncertain multiple attribute decision making models[J].System Engineering—Theory & Practice，1999，19(12)：42-47(in Chinese).