薛凤祚《正弦》一书研究

杨泽忠

(山东师范大学数学科学学院，山东济南 250014)

薛凤祚《正弦》一书研究

杨泽忠

(山东师范大学数学科学学院，山东济南 250014)

《正弦》是薛凤祚的重要译著之一。深入分析此书中的内容、方法和数值等，可以发现，尽管书中给出的内容稍显繁乱，但思路是明确的，方法是科学的，计算是正确的;书中内容主要来自斯蒂文的《数学记忆》一书第一部分的第一卷“正弦表制作方法”;薛凤祚在编译此书时并非墨守成规，而是在底本方法的基础上给出了一种更为合理和经济的新方法，以精密快捷的计算推进了当时正弦函数造表方法的研究。

薛凤祚;正弦;制作方法;三角函数

一、引言

在薛凤祚的《历学会通》中有《正弦》一卷。此书主要介绍了西方正弦函数表的做法，是薛凤祚和穆尼阁的重要译著之一。薛凤祚在此书的序言中说:“天文各线皆圈线也，而各种取用之嫌，以方代圆，所差甚微。作法者殆疑神授，非人力也……往年予与穆先生重译于白下，今天学且竣，溯流穷源更授此学，弁诸法之前。”①薛凤祚:《正弦法原叙》。可是，长期以来却少有对此书的研究。仅有的个别研究得出的结论还是消极的，如清初历算名家杨作枚曾说:“薛青州做正弦解，亦仅依式推衍，未能有所发明。”②梅文鼎:《解八线割圆之根》，《兼济堂篆刻梅勿庵先生历算全书》，咸丰九年(1859)。李俨也说:“(薛凤祚的做正弦表方法)大致本诸《大测》。”③李俨:《中算史论丛(第三集)》，科学出版社1954年版。此书是否真的如上所说?笔者在研读此书时发现并非如此，本文拟就这个问题做一阐述，以求教各位方家。

二、《正弦》的主要内容及科学性

《正弦》一书共分六部分，即:正弦解释;求间隔三度七十五分的正弦函数值;求间隔七十五分的正弦函数值;求间隔二十五分的正弦函数值;求间隔一分的正弦函数值;正余割和正余切函数，主要介绍了正弦函数的概念、几何意义和九十度以内值的算法，其它部分不及整个篇幅的十分之一。

其求正弦函数值依据的基本原理是单位圆内正弦函数的几何意义。文中作者说:“各度数之弦即线之半……此作表之根。”文中使用的公式有五个，即:

文中给出的求九十度内正弦函数值的做法程序是:

首先，规定将圆半径分为10000000份，圆周分为90000(先分为90度，然后每度再分为100份)。利用正弦定义，得出九十度的正弦值。

其次，通过做圆内接正六边形，得出六十度圆心角所对的弦长，然后根据基本原理，得出三十度的正弦值。并利用公式1和2得出六十度的正弦值。

第三，根据正弦定义和基本原理求出了四十五度的正弦值。

第四，利用公式3求出十五度、七度五十分、三度七十五分、二十二度五十分和十一度二十五分的正弦值。

第五，利用十五度和三度七十五分的正弦值再求出与之相关的正弦函数值。

第六，藉此再求出了它们的余角和余角半角的正弦函数值。至此“隔三度七十五分表已具。”

第七，通过做圆内接正五边形，求出三十六度的正弦值。

第八，用上述公式，求出其半角、半角的半角、半角的半角的半角……的正弦值，再求出其余角的正弦值，再求出其余角半角或其半角的半角的正弦值。

第九，利用三十度和五十四度的正弦值与公式4求出12度的正弦值。

第十，利用公式1、2求出十二度的半角、半角的半角……的正弦值，求出其每个余角的正弦值，再求出其余角每个半角或余角等的正弦值。至此“以上共一百二十，前后皆隔七十五分。”

第十一，利用七十五分和一度五十分的正弦值，构造如下的差分公式求出了一度的正弦值，并求出了五十分的正弦值。

十二，利用五十二度五十分和五十分的正弦值，运用公式4再求出二十六度的正弦值，又利用公式1、2求出了六十四度的正弦值。

十三，“以下平分，隔二十五度表皆全。”

十四，其它未知角度的正弦值可用公式5求出。比如

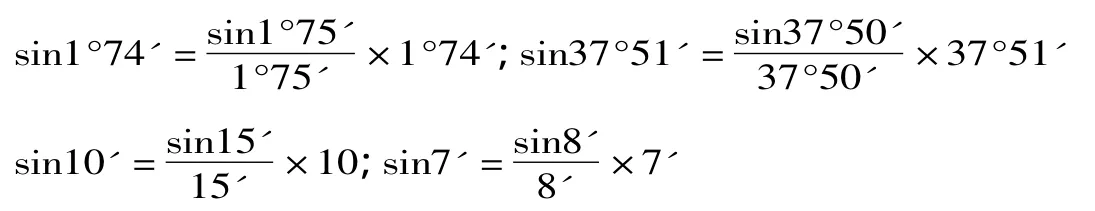
这个程序能否求出全部的九千个正弦函数值呢?经笔者验证，完全可以!利用通过几何意义得到的九十度、六十度、四十五度和三十度的正弦值，反复使用前三个公式可以求出九十度内容间隔三度七十五分的所有二十四个正弦值。利用三十六度的正弦值，反复应用前三个公式，又可求出三十二个正弦函数值。求出十二度的正弦值之后，再反复使用前三个公式，又可求出六十四个正弦值。这样间隔七十五分的正弦值就全部求出了(见附录一)。然后，待一度的正弦值求出，利用上述公式又可得到四个角度的正弦值。待二十六度的正弦值求出之后，反复使用前三个公式，又可得到一百九十二个角度的正弦值(见附录二)。这样间隔二十五分的共计三百六十角度的正弦值基本上就全部求出了。最后，再利用公式五即可求出全部的间隔一分的正弦函数值。

另外，笔者将《正弦》一书中给出的间隔七十五分角度的正弦值逐一进行了比较，发现其与利用现代工具计算器求得的值几乎完全一致，仅有八个值有误差，并且误差也多在10－6即百万分之一以下。

所以，《正弦》一书给出的方法尽管略显繁杂，但其合理性、科学性和可操作性均不容怀疑。

三、《正弦》一书内容的来源

《正弦》一书给出的方法来自哪里?是否诚如前人所说“本《大测》诸法”?笔者认为这要看两个方面:一是二者的方法是否一致——毕竟《大测》一书成书在前，《正弦》一书成书在后;二是二者的来源是否相同。

《大测》一书成于1630年左右，早于《正弦》成书20余年，是瑞士传教士邓玉函(JohannTerrenz，1576—1630)为《崇祯历书》的编纂而撰写的。此书主要介绍了三角函数的概念和正弦函数的造表法，书中给出的正弦函数造表程序是:

首先，将半径分为10000000份。然后做圆内接正三、四、五、十和十五边形，求得其边长对应的份数，再然后利用正弦函数的几何意义求得六十度、四十五度、三十六度、三十度、十八度和十二度的正弦值。这种方法在《大测》中称之为“六宗率”。

其次，对于其它三角正弦值，利用以下六个公式求出:

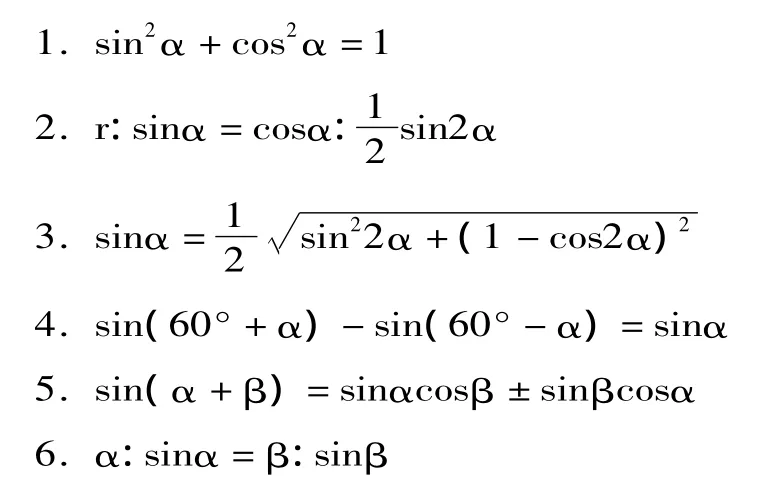
作者称前三个公式为“三要法”，后二个公式为“二简法”。

作者说:“有前六宗率为资，有后三要法为具，即可作大测全表。”在此后作者举例给出了九十度内由十二度衍生出来的50个正弦函数值(六十进制的，最小的为45分的正弦值)。并说:“其余五形如三边、四边、五边、六边、十边形亦如前法作此，既毕即大测表之大段全具矣。”①邓玉函:《大测》，《新法算书》。

第三，至于每一分的正弦值，作者介绍说可用比例法，也就是可用公式6便可求出。

由此看出，《正弦》一书中给出的正弦值的求法的确与《大测》一书中给出的方法在某些方面有些相似，比如二者都是从三角函数的几何意义出发的，都使用了正余弦函数关系的公式，都使用了相同的正弦半角公式，都对小角度使用了比例法，都有着相同的思路等。但是，二者还是有着明显的不同。

首先，《大测》一书使用了做圆内接正十边形来求十八度，《正弦》一书没有;第二，《大测》一书使用了上述公式4和5，而这在《正弦》一书中没有;第三，《正弦》一书中求十二度的正弦值使用的是两角差的半角公式，而不是作圆内接正十五边形求半角的方法;第四，《正弦》一书中利用两角差的半角公式计算了二十六度的正弦值，而这在《大测》中没有。所以，说《正弦》一书的方法“大致本《大测》诸法”从内容上来看极为牵强。

下面再来看二者的来源。关于《大测》的来源，经白尚恕先生考证，其底本主要是波兰数学家毕的斯克斯(B．Pitiscus，1561—1613)于1595年写成的《三角学》一书(Trigonometriae)②白尚恕:《介绍我国第一部三角学——〈大测〉》，《数学通报》1963年第2期。。其内容主要编译于其第一部分(共三部分)的第二卷(共五卷)。那么薛凤祚《正弦》一书的内容来自哪里呢?此前尚无有研究。为了弄清这个问题笔者对明末清初之际西方传教士带来的西方三角书籍进行了检查，并根据数学史提供的线索对西方十八世纪之前出现的三角学著作也做了大量排查，最终发现，薛凤祚的《正弦》一书内容与十六世纪末期荷兰数学家斯蒂文(S．Setvin，1548—1620)于1608年出版的《数学记录》(Hypomnemata mathematica)中的部分内容非常相近。

斯蒂文于1548年生于比利时，1577年定居于荷兰。其以机械制作和工程建筑闻名于世。也许由于工作的原因，其特别重视数学和物理学。在物理上，其深入研究了静力学和流体力学，早伽利略五年做过“两个铁球同时落地”的实验。在数学上，其深入研究了小数，在欧洲出版了第一部关于小数的著作《论十进》(La Theinde，1585)。此外，其还研究过透视学、极限方法、声乐和辩论术，在历史上第一次使用了加号“+”、减号“–”和开方符号“√”等等③Simon Stevin．http://www － history．mcs．st－ andrews．ac．uk/Biographies/Stevin．html，2009 －12 －12。。

《数学记录》是一部数学著作合集，共包含了斯蒂文的三部数学著作，即:《三角学》、《测量学》和《透视学》。此书最初版本是德文的，同年即被翻译成拉丁文和法文再版，由此可略见此书在当时的受欢迎程度。此书被翻译成拉到文之后在欧洲学术界广泛传播。明朝末年金尼阁(Nicolas Trigault，1577—1628年)等西方传教士来中国之际也将此书传播到了我国，现在在北堂图书馆馆藏中就有此一本。据我国数学史家白尚恕先生研究，邓玉函在编写《大测》时还曾参考过此书。

此书的第一部分《三角学》又分为四卷，第一卷名称为“正弦表制作方法”(Sinuum Canonibus Fabricandis);第二卷名称为“平面三角”(Triangulis Planis);第三卷名称为“球面三角”(Spaericis triangulis);第四卷名称为“天球问题”(Caelestium sphaerarum problematis)。在第一卷“正弦表制作方法”中作者给出一个九十度内间隔一分(六十进制)的正弦函数表、一个正切函数表和一个正割函数表。在正弦函数表之前，作者对于如何求出正弦函数进行了详细说明。

首先，作者给出了九个与三角函数有关的定义，有:弧角(Arcus anguli，est segmentum semiperipheriae a cruribus comprehensum，e vertice anguli tanquam centro delineatae)、正弦(sinus，est recta ab arcus termino in diametrum perpendicularis)正矢(Sinus－sagitta est segmentum diamctri a perpendiculo sinus perpheriam)、余弧(Arcus differentiae，est differentia positi arcus a quadrante)、余角(Angulus differentiae，est differcentia positi anguli a recto)补角弧(complementum semiperipheriae，est arcus qui dato additus semiperipheriam complet)正切角(Tangens anguli，est recta parallela sinui，altero termino tangens extremum arcus anguli＆ intercepta a reliquo crure ulterius producto)、正割(Secan，est anguli crus alterum ad tangentem usque extra peripheriam productum)、已知直线或角(Cognitas lineas aut angulos dicimus，quorum quantitas numero explicatur)。

然后作者给出了十个命题，并都给出了具体解释和证明:

1．Cognitis semidiametro＆sinu anguli differentiae sinum cognitum reddere(已知半径和一个角的正弦，则其余角的正弦可求出);

2．Cognita sagitta＆semediametro:sinum semissis eiusdemarcus cognitum reddere(已知一个角的正矢和半径，则这个角一半的正弦可求出);

3．Ccognitis semidiametro，＆ duorum arcuum，＆ arcuum differentiae sinibus:chordamarcus quainter se discrepant invernire(已知半径和两弧以及它们余角的正弦，则两弧之间的弧所对的圆心角的一半的正弦可求出);

4．Posita semidiametro circuli 1000000000:＆ sinus＆ arcuum differentiae sinus e continua bisectione 90 graduum derivatorum，donec ad impairs numeri scrupula prima deventum sit，invenire(假设圆的半径分为1000000000，则90度的半角和半角的半角以及这些角的余角的正弦都是可以求出的);

图1

5．Posita semidiametro circuli 1000000000:arcus 36 grad．＆ arcus differentiae sinum，omniumquearcuum，＆arcuum differentiae e continua bisectione 36 grad．derivatorum，donec ad impairs numeri scrupula prima deventum sit，sinu invenire(假设圆的半径分为1000000000，则36度及其余角的半角和半角的半角以及这些角的余角的正弦值都是可以求出的);

6．Posita semidiametro circuli 1000000000:arcus 30 grad．＆ arcus differentiae sinum，item omniumarcuum，＆ arcuum differentiae sinus e continua bisectione 36 grad．donec ad impairs numeri scrupula prima deventum sit，derivatorum sinu invenire(假设圆的半径分为1000000000，则30度及其余角的半角和半角的半角以及这些角的余角的正弦值象36度角那样也都是可以求出的);

7．Posita semidiametro circuli 1000000000:arcus 12 grad．＆ arcus differentiae sinum，item omniumarcuum，＆ arcuum differentiae sinus e continua bisectione 12 grad．donec ad impairs numeri scrupula prima deventum sit，derivatorum sinu invenire(假设圆的半径分为1000000000，则12度及其余角的半角和半角的半角以及这些角的余角的正弦值也都是可以求出的);

8．Si in quadrante circuli perpendiculars a terminis aequalium arcuum secent semidiametrum，segmentum propius centro erit majus remotiore(四分之一圆中从相等的两段弧的两端向半径做垂线，得到的两个线段中，靠近圆心的大于另外一条);

9．Posita semidiametro circuli 1000000000:1 grad．＆ arcus differentiae sinum，item omniumarcuum，＆ arcuum differentiae sinus e continua bisectione 1grad．donec ad impairs numeri scrupula prima deventum sit，derivatorum invenire(假设圆的半径分为1000000000，则1度及其余角的半角和半角的半角以及这些角的余角的正弦值也都是可以求出的);

10．Ad inventos sinus aequali intervallo 15’crescents:reliquos minutim ad scendentes addere(15’以内的每一分的的正弦值已知了则其余的比较小的角度的正弦值即可求出)．

在命题1的证明中作者在说明勾股定理的基础上给出并使用了两个公式α)=cosα。

在命题4的证明中作者利用上述半角公式给出了四十五度、二十二度三十分(六十进制的)、六十七度三十分、十一度十五分、七十八度四十五分、三十三度四十五分和五十六度十五分的正弦函数值。

在命题5中作者通过分析圆内接正五边形的边长，给出了与三十六度相关的三十二个角度的正弦值，如图1所示。(至此间隔三度四十五分的所有角的正弦值都求出。)

在命题6的证明中作者首先利用圆内接正六边形的性质，求出了三十度的正弦值，然后又利用上述半角公式给出了十八个与三十度有关的半角和余角正弦值。

在命题7中作者利用五十四度和三十度的正弦值，命题三中的公式计算出了十二度的正弦值，并给出了与之相关的六十四个正弦值。

至此，作者说间隔四十五分(六十进制的)的正弦函数值共一百二十个就全部算出来了。

在命题9中，作者结合命题8利用四十五分和一度三十分讨论了1度角的正弦值，最后利用如下平均数公式求出了1度的正弦值:

并由此讨论了半角三十分的正弦值和十五分正弦值。并在后面详细介绍了比较小的正弦值的求法(Defabrica sinuum):比例法(Si qua dubitation ex istiusmodi ratiocinio existere posset)。即相近的两个角度的正弦值可用如下公式来计算:α:sinα=β:sinβ

在命题10中，作者利用上述公式详细说明了每一分正弦值的求解方法。

由此，可以看出在具体的正弦值的求解思路上，薛凤祚介绍的和本书作者给出的完全一致。二者都是从求九十度、四十五、三十度、十二度等特殊角开始的，都主要使用的是上述五个公式。都是先求出间隔三度四十五分角的正弦值，再求出间隔四十五分的角的正弦值，然后再求出一度角的正弦值，最后利用比例法求出间隔一分的角的正弦值。

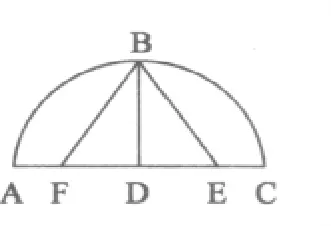
图2

这个过程中，使用的公式二者使用的公式完全一样。

另外，在具体细节方面，二者在一些地方更是极为接近。比如在讨论圆内接正五边形的边长时，这里斯蒂文使用托勒密的方法给出了五边形边长的具体做法，薛凤祚的介绍中也给出了具体做法，并且做法完全一致。这里作者给出的做法是:“Descripti semiciirculi ABC，semidiametros DC valet 1000000000，e cuius centro D educta BD perpedicularis sit diametro AC:＆E punctum bisecans semidiamctrum DC，connectatur cum B，ductaeque EB aequalis sit EF secan diametrum in F，recta ab F ad B erit latus quinquanguli ordinate in circulum cuiusdiametros;est AC inscrupti，demonstramte Ptolomus cap．9．lib．1．magnioperis．Quare inventa BF，cognita erit chorda72 grad．”书中给出的图形如图2所示。①S．Stevin．Hypomnemata mathematica．Leyden:Jean Paedts，1608．7 －8．

图3

这段话的意思说:如图所示，画一个半圆ABC，半径DC的值为1000000000，圆心为D，做BD垂直直径AC。设E点是半径DC的中点。将其与B连接，做与EB相等的线段EF，设其交半径于F点，则FB的长即等于圆内接正五边形的长(证明可见托勒密的书第一卷命题9)，弦BF对应的圆心角为72度。

薛凤祚给出的做法是:“先画巳子丑半圈，丑、寅、卯、辰、巳分径。卯丑卯子皆为通弦。先分巳卯为二，即巳辰、辰卯。从辰作子辰线，辰至子与辰至寅等。寅至子亦等。以线论分，卯寅即圈十分之一，寅子即圈五分之一。”薛凤祚给出的图形如图3所示。

还有在利用平均数来求一度的正弦值方面二者也是极为一致的。斯蒂文使用的是如图4所示的图形。在这个图形中，AC分为1000000000，弧BE为一度三十分，其正弦是DE，为26176948。弧BF是四十五分，弧BG为一度，DI为一度的正弦，将弧BF三等分，得到K、L两个点弧。GE的中点为M。三等分DH即四十五分的正弦13089622，得OH为4363207。用OH的长度近似代替HI的长度，则得到DI近似等于17452829。因为OH的长度略大于HI的长度，因此得到的DI略大于实际值。用DE的长度减去DH的长度得到HE的长度为13087326，将其三等分得HI为4362442，由此得到略小于实际值的DI为1745064。求略大值和略小值的平均数，则得到一度的近似值174524。①S．Stevin．Hypomnemata mathematica．Leyden:Jean Paedts，1608．13 －14．(此处原文较长，故不录述。)

薛凤祚使用的是如图5所示的图形。在这里薛凤祚说:“如图，子丑一度五十分，酉乙一度，酉寅一度五十分(百分制)。酉甲七十五分，又分为三，每分二十五分。申寅一度五十分正线，申辰一度正线，申巳七十五分正弦，今求申辰一度正弦。

先有申巳七十五分正弦一三〇八九六，以三分之为四三六三二为二十五分略大者线。

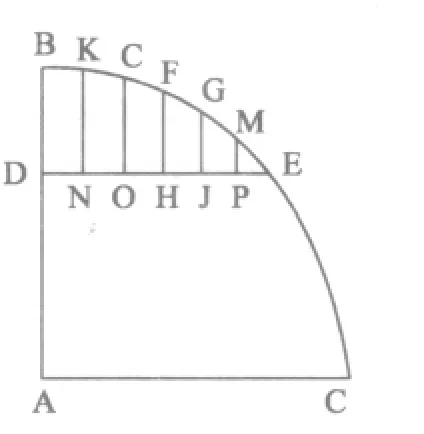
图4

先有申寅一度五十分正弦二六一八六九，内去七十五分正弦一三〇八九六，余一三〇八七三，用以三分之为四三六二四，为二十五分略小者线。稍大者之半即一度正弦一七四五二四。”

由此，薛凤祚的说法虽然简单，但做法完全一样，并且其中的说法和数值也基本上一样的——不计数字位数和进位制。

另外，二者的这种一致性至今未在其它的文献中发现。

因此，薛凤祚《正弦》一书的底本基本可以认定是斯蒂文的《数学记录》中第一书的第一卷《正弦表制作方法》。《正弦》一书的内容应是薛凤祚和穆尼阁二人在学习《正弦表制作方法》的基础上又结合个人的想法(主要是将六十进制改为百进制)而编译的——正如此书的署名的提示(南海穆尼阁编，北海薛凤祚注)。

既然如此，那么当十分肯定的说《正弦》一书给出的正弦函数表制作方法绝非源于邓玉函的做法，而是别有来源。

图5

四、薛凤祚对于正弦函数表做法的研究

由上可以看出，薛凤祚《正弦》一书的内容主要取材于斯蒂文的《正弦表制作方法》，但二者还是有些地方不一样。哪些地方不一样?我们做了一下统计，发现主要有两个方面:第一，《正弦》一书将角度由原来的六十进制(度以下)改为了百进制。第二，《正弦》一书增加了二十六度角正弦值计算。

关于第一个方面，诚然有薛凤祚的解释:“旧法又以六成十不能相入，乃取而通之。”②薛凤祚:《中法四线》叙言。但笔者认为应该还有第二层意思，即是完成前人的心愿，推进前人的研究。

邓玉函于1630年写成《大测》时说:“已上所述皆远西法也，彼自度以下遁析为六十，今中历遁用百析。为便故须会通前表为百分之表。其会通法如西六十分即中之百分，半之三十分即五十分……”③邓玉函:《大测》，《新法算书》。在这里很明显邓玉函发现了中西法的不同，并明确给出了两种进制的会通办法，但是，其终未能给出会通的结果，更未给出会通之后的正弦函数表——不能不说是一个遗憾。

还有，在《正弦》一书的序言中薛凤祚曾说:“今旧法割圆表久镌行世，而独遗取正弦之法，盖秘之也。学者求其法而不得，将并所用之法而不敢信，非作与传之过欤。”①薛凤祚:《正弦法原叙》。

因此，薛凤祚的改制应该有完成前人未尽之事业以细致的工作切实推动当时中西数学的会通之意义。

关于第二个方面，笔者翻阅了斯蒂文《正弦表制作方法》、邓玉函《大测》、毕的斯克斯的《三角学》以及布里格斯的《不列颠三角学》(Trigonometria Britannica)等书，均未发现有雷同做法，薛凤祚在制作正弦函数表过程中引入二十六度作为特殊角尚属首次。

薛凤祚利用两角差的半角公式计算出二十六度的正弦值，以二十六度为一个特殊角来计算正弦值有什么意义呢?

为了弄清这个问题，笔者沿着书中给出的思路——即是知道了一个角的正弦值之后再利用半角公式求其半角的正弦、半角的半角正弦、半角的半角的半角的正弦……，然后再利用余角公式和余角的正弦公式求其余角的正弦、所有半角余角的正弦、所有余角半角的正弦，等等——进行了分析，发现这一步是非常关键的一步，至关重要。

这是因为，二十六度角的正弦值求出之后，按照上述思路即可求出一百九十二个新的不同角度的正弦值。这些角度的正弦值与前面的一百二十个并不重复。这样，将这二者合并起来，则(九十度内)间隔间隔七十五分和二十五分的角度的正弦值就基本齐备了——因为九十度以内间隔二十五分的角度共三百六十个，现在已有了三百一十二个，已达到了总体数值的百分之86．7%。而直接由二十六度出发求出的角度的正弦值又是其中的百分之61．5%，是整体所有值的53．3%。由此，二十六度角是上述算法中非常关键的一个角度，这个角度正弦值的求得，能极大的促进整体角度值的快速求出。

由此看出，薛凤祚在《正弦》一书中结合前人的理念，在具体计算方法上实际上给出了一条有别于底本作者的和其他人的新的途径，即是:

为计算九十度以内所有角的正弦值，先计算出与九十度、六十度、三十六度和十二度相关角(半角和余角)的正弦值，得到全部间隔三度七十五分的正弦函数表;

然后求出二十六度角和四十度(四十度角按照上述思路可以衍生出其余四十八个角度的正弦值，见附录三)相关角的正弦值，将这些值与前面角度的正弦值相补，得到全部间隔二十五分的角度的正弦值;

再然后根据比例法求出二十五分之内角度的正弦值。

这种做法与斯蒂文和邓玉函的做法明显不同。斯蒂文和邓玉函都是在进行了第一步之后差不多就开始用比例法了，没有薛凤祚方法的第二步。另外，这两种途径比较，很显然薛凤祚的更为清晰，充分展示了正弦函数表由特殊到一般，由疏到密的一般的制作方法。还有，薛凤祚给出的这种途径很显然也是更为快捷的和经济的，因为其有很强的规律性和程序性。

由此，笔者认为薛凤祚在这里改革了前人的工作，另辟一条蹊径，给出了一条更为清晰和全新的思路，提高了计算速度，以出色的工作切实推进了当时正弦函数表的制作方法——《正弦》一书中不能说没有薛凤祚的研究和创新。

五、结论

通过上述分析，薛凤祚的《正弦》一书虽然和邓玉函的《大测》在内容思路上有些相近，但由于二者存在明显的不同，且来源不一样——《大测》一书的底本是毕的斯克斯的《三角学》，而《正弦》一书的底本是斯蒂文的《数学记录》，故《正弦》中的方法绝非由《大测》中的方法而来。《正弦》一书在成书过程中，将度之下的六十进制改为了百进制，由于有前人的提示，应该有进而推之完成前人之遗愿的意义。但是，书中首先使用了二十六度做为特殊角来帮助计算间隔二十五分的角度的正弦值显然是个创举。藉此，作者实际上给出了一条比底本作者和其他学者更为清晰和快捷的计算路径，提高了计算效率，不仅切实推进了正弦函数值的计算，而且也推进了当时正弦值计算方法的研究，做出了自己的贡献。由此，笔者认为对于薛凤祚的研究还是《清史稿》中给出的评价更为中肯，《清史稿》中讲:“凤祚定岁实秒数为五十七，与奈端合，与穆尼阁以为四十五秒者不同，则其学非墨守穆氏可知。或讥其谨守穆尼阁成法，依数推衍，非笃论也。”②赵尔巽:《清史稿》卷五百零六，列传二百九十三。这里虽然说的是薛凤祚的天文学，其实对于其在数学方面的会通工作也是完全合适的。

K23

A

1003－4145［2011］06－0044－07

2011－03－03

杨泽忠(1968—)，山东肥城人，山东师范大学数学科学学院教授、博士，主要研究方向:数学史、数学教育。

(责任编辑:陆影luyinga1203@163．com)