脉宽调制器中一类振荡器的全面解析结果

2011-11-27孙定浩

空间控制技术与应用 2011年5期

关键词：将式特征参数表达式

孙定浩

(北京控制工程研究所，北京100190)

脉宽调制器中一类振荡器的全面解析结果

孙定浩

(北京控制工程研究所，北京100190)

用分析法全面讨论脉宽调制器(IC:1842/3/4/5，1842A/3A/4A/5A)中振荡器的振荡特征参数(占空比D和频率f)与外接电阻R和电容C的关系.我们得到以R、C为自变量表达D和f的函数，以D、f为自变量求R、C的函数.并根据这些函数的计算结果绘制描述D、f、R、C(1F)4个参数之间的关系曲线.这些结果，不仅提升了对这类振荡器的认知，而且可供设计时直接引用和参考.

脉宽调制器;184X(184XA)集成电路;振荡器

关于脉宽调制器(IC:1842/3/4/5，1842A/3A/4A/5A)中振荡器的振荡特征参数(占空比D和频率f)与外接电阻R和电容C的关系，至今只见生产厂根据实测数据绘制的一组曲线，以及一个当R＞5kΩ时用RC乘积表达f的近似式[1].

本文基于这类振荡器的电路模型，首先设R、C满足振荡条件，建立振荡方程，解出以R、C为自变量求D和f的表达式，以及以D、f为自变量求R、C的表达式.基于这些表达式，得到了这类振荡器振荡时R、C应满足的条件，绘制了184X和184XA振荡器D、f、R、C(1F)4个参数之间的关系曲线.接着分析R不满足振荡条件时这类振荡器的非振荡运行特性.从而在R＞0，C＞0全范围内阐明了这类振荡器的运行规律.

本文分析所得的表达式以及绘制的4个参数关系曲线，不仅提升了对这类振荡器的认知，而且可供设计时直接引用和参考.

1 一类振荡器模型及等效电路

图1(a)、(b)示出184X(184XA)振荡器电路模型.设

a.E＞VH＞VL＞0;

b.当V0处于低电平，Q的ce断开，此时ce间电阻无限大;

c.当V0处于高电平，Q的ce导通，由于Vce约在1～2.7V之间运行以及Q是受一固定的基流驱动，故此时Q的ce间等效于一恒流‘井'i，它与C并联.

因此，振荡器在Ton(V0低电平)时段和Toff(V0高电平)时段的等效电路如图1(c)所示，图1(d)示出振荡时Vc(t)的波形.

图1 振荡器电路模型及等效电路

2 振荡方程及解析解

按图1(c)得下列振荡方程组:

Ton时段:

起点:

终点:

Toff时段:

起点:

终点:

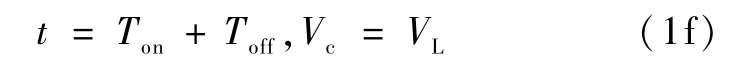
根据式(1b)解式(1a)，得Vc(t):

将式(1c)代入式(2)得

由式(1e)解式(1d)，得Vc(t):

将式(1 f)代入式(4)得

因此，占空比D和频率f表达如下:

由式(6)知，D与R有关，与C无关.因此，以后将D写成D(R)，它表征了占空比与R的关系.式(6)对R微分得

另一方面，将式(7)改写成

其中:

因此，f与R、C的关系可分解为f与C成反比，f与f(R，C=1)成正比.f(R，C=1)的物理意义是当C=1F时的f值;函数符号中C=1只是为了明确表示函数的意义.

将式(6)代入式(10)得f(R，C=1)与D(R)的关系:

3 振荡条件及D(R)和f(R，C=1)函数特性

现根据式(6)、(10)以及下列两个限制条件寻找发生振荡的R和C范围.

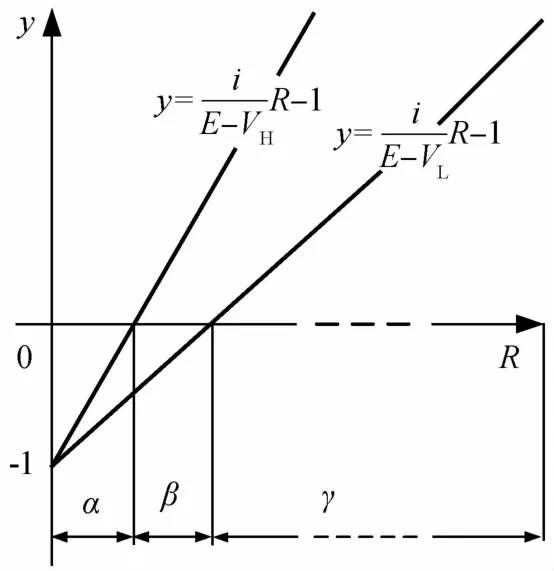
图2 R＞0的3个区间α、β和γ

图2示出式(6)中包含的两个线性函数:

它们将R轴分成3个区间α、β和γ.由式(6)、(8)可知各区间的D(R)和d D(R)/d R的值.

区间α(0＜R＜(E-VH)/i):D(R)＜0.

区间β((E-VH)/i＜R＜(E-VL)/i):D(R)值不存在.

区间γ(R＞(E-VL)/i):

由式(14)知，在区间γ，D(R)由趋于零开始随R增大单调增大渐近趋于1，满足条件(12).将式(12)代入式(11)知，在区间γ，f(R，C=1)＞0.由于存在关系式(9)，故知使f＞0的必要条件是C＞0.综上所述，发生振荡的充要条件是现在讨论在γ区间f(R，C=1)函数特性.根据

式(11)和上述D(R)特性可知:

f(R，C=1)是连续函数，故它在区间γ内有极大值.

4 R(D)和C(R，f=1)函数

设计振荡器时更需要以D和f为自变量求R和C的表达式.由式(6)得

由式(9)、(11)得

其中

式(11)中R是自变量，但在上式中将D作为自变量，故将式(11)的D(R)和R分别改写为D和R(D)，R(D)由式(17)给定.由式(11)(18)得

5 计算结果图示

取一组典型值:

根据式(6)、(10)计算值绘成图3.

图3 关系曲线图

6 振荡特征参数与R、C的关系

式(6)、(10)和图3即可全面说明振荡特征参数与R、C的关系.

1)当R＞(E-VL)/i，C＞0，理论上振荡发生.文末将讨论由于噪声的存在，实际上能产生稳定振荡的R的最小值.

2)关于占空比:

a.D只与R有关，与C无关.

b.D随R增加单调上升渐近趋于1.

3)关于频率:

a.f与C成正比.

b.当C给定，R值可分两个区间，在R值小的区间，R增加f增大;R值大的区间，R增加f下降.两区间交界处f最高.数值结果显示，在f最高处184X或184XA的D值均约0.5.

可以认为，R值是决定D和f的‘首要'外接参数，它决定D，同时又决定C=1时f值;C值的作用只是R值确定后实现所需的f.

4)关于D=0.5:

大量实际电路中R均几kΩ，即D≐0.9.当需PWM最大占空比约0.5时，一种方法是用1845(1845A)，R值依然取几kΩ，PWM的最大占空比约0.5，但PWM最高频率约为250kHz.另一方法是将1843A(设电源电压10V)应用于D=0.5，此时R约750Ω.从基准源(5V最大输出电流20mA)流向R的平均电流为4 mA.1843A为外接R、C而增加的功耗28mW.这些都是1843A允许的.另一方面，由式(2)、(4)知D=0.5时Vc(t)近乎对称的三角波如图1(d)所示.这种方法实现了D=0.5，但PWM频率仍等于振荡频率，最高频率500kHz.

5)当C给定，R给定且大于3kΩ，184X和184XA的振荡频率差小于3%，占空比差小于0.05.一般情况下，此时184X和184XA可以互换.当R＜1 kΩ，这两者振荡特征参数相差较大.

7 非振荡运行α、β和γ

当R在区间α，E-VH-iR＞0，由式(4)知，Toff时段V(t)从VH开始后不是下降而是指数上升，渐近线在Vc=E-iR＞VL，故不能发生振荡.当R在区间B，E-VH-iR＜0，由式(4)知，Toff时段V(t)从VH开始后虽指数下降，但渐近线在Vc=E-iR＞VL，也不能发生振荡.仅当R在区间γ，渐近线满足条件Vc＜VL，振荡发生.

图4在相平面(Vc，V0)中描述了这3种运行模式.起点均设在Vc=0，粗细表示运行相迹，S是稳态工作点.

综上所述，图5以R为自变量，在R＞0，C＞0范围内对这类振荡器Vc的稳态作了一种描述，其中实线表示Vc稳态直流电压值;两虚线表示振荡发生，纵坐标分别表示Vc(t)振荡对地的峰值和谷值.

图4 在(V c，V0)相平面中振荡器运行的3种相迹图

图5 V c稳态值与R、C(作为参量)的关系

8 讨论R的实际最小值

由式(2)知，即使在R=(E-VL)/i+且ε→0时，Ton并不趋于零;此时D→0，由式(4)知是由于∞的结果.

图6 从V H开始经三倍时间常数到达V L的V c(t)曲线

图6示出在Toff时段Vc(t)从VH开始以三倍RC时间常数到达VL的过程.考虑到图1(a)中噪声、干扰等对触发器在VL处触发的影响，一般认为这样的Vc(t)在Vc=VL附近变化过于平缓，实际触发点已不稳定，因而f也不稳定.用Toff=3RC作为估算形成稳定振荡的临界条件，由式(4)得

由此得R的实际最小值为

将式(20)、(21)所列典型值代入得，184X的m in R=315Ω，184XA的m in R=493Ω.由图3知此时两者的D值均约为0.16，这就是实际形成稳定振荡的最小占空比.

[1] Unitrode Integrated Circuits Corporation(UICC).Productamp;applications hand book[M].1993～1994，5-190

Completely Analytical Results of a K ind of Oscillators in Pulse Width Modulators

SUN Dinghao
(Beijing Institute of Control Engineering，Beijing 100190，China)

In this paper，the relations between the oscillation characteristic parameters(duty ration D，frequency f)and the parameters R and C connected with the oscillators in PWM(IC:1842/3/4/5，1842A/3A/4A/5A)are completely discussed by means of the analytical method.Representations of D and f taking R and C as arguments，and representations of R and C taking D and f as arguments are obtained，and then based on the calculations of these representations，the curves for describing relations among the four parameters D、f、R、C(equal to 1F)are drawn.These results not only greatly promote understanding of the oscillators，but also can be immediately quoted and referred during design.

pulse width oscillators;IC:184X(184XA);oscillator