基于宽带宽测量的姿态确定方法

2011-11-27何世民

空间控制技术与应用 2011年5期

关键词：卡尔曼滤波陀螺宽带

何世民，汤亮

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

基于宽带宽测量的姿态确定方法

何世民1，2，汤亮1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

针对由飞轮等星上高速旋转部件所引起的高频姿态和指向抖动，提出一种基于磁流体动力学特性的角位移敏感器用于星上高精度宽带宽的微振动测量，以弥补常规姿态测量系统测量频带低，动态范围有限的缺点.介绍以扩展姿态确定带宽为基础的高精度姿态确定方法.给出了以陀螺、星敏及ADS测量信息为基础的宽带宽的姿态确定方法及系统的模型，采用了卡尔曼滤波来确定卫星姿态.仿真分析结果表明存在高频姿态抖动的情况下，宽带宽的姿态确定方法的估计精度优于传统的姿态确定方法，由此验证了宽带宽的姿态确定方法的有效性及精确性.

高频姿态抖动;宽带宽的姿态确定;卡尔曼滤波;ADS

在对地观测领域，人们为了获得更高的分辨率而不断努力.由于空间分辨率的提高，观测图像几何精度的重要性变得更加显而易见.卫星的这种高分辨率的特点就要求卫星在没有地面控制点的情况下进行精确的地质测量和几何校正，为达到此目标，就要指定一组严格的精度指标，包括姿态确定精度要求、指向精度要求、指向稳定度要求、姿态抖动指标要求等[1-3].

一方面由于卫星结构的复杂化，来自卫星本身及外部环境的扰动具有比较宽的频率范围.另一方面，飞轮系统因其内部多种因素影响而产生包含多种频率成分且频率值较高的振动.由于这些因素产生的高频姿态和指向抖动是姿态确定精度和有效载荷指向精度所面临的严峻挑战[3].目前采用陀螺、星敏、太阳/地球敏感器等多种敏感器组合定姿的方法是航天器高精度姿态确定的常用手段，但其测量带宽被限制在几十赫兹以下，高频的微振动则被当作噪声滤掉，这远远不能满足高分辨率卫星姿态确定精度和有效载荷指向精度的要求.

为提高姿态确定和有效载荷指向精度，国内外很早就研究对高频姿态抖动的测量方法及建模技术.文献[4]提出了测量并在对地观测中补偿这种高频抖动的方法来提高卫星姿态确定精度和有效载荷指向精度.日本于2006年1月发射的ALOS上安装了ADS和加速度计用于在轨测量高频抖动，实现了10-6(°)量级抖动角度的在轨测量.通过分析获得的遥测数据，对姿态动力学与干扰进行更加准确地建模和参数辨识[5].文献[3]给出了采用ADS测量高频姿态抖动，用于扩展姿态确定带宽的思想，给出了融合低/高频姿态信息的滤波方法.

本文在前人研究的基础上，推导了基于陀螺、星敏感器和ADS测量的宽带宽的姿态确定方法，详细论述了基于卡尔曼滤波的宽带宽的姿态确定算法.最后对融合高频姿态测量信息及不融合高频姿态测量信息两种情况进行数学仿真和比较分析，结果表明，以卡尔曼滤波为基础的融合结果可得到较高的估计精度，从而验证了宽带宽姿态确定的有效性及精确性.

1 问题模型

1.1 陀螺与星敏感器的测量模型

高精度卫星姿态确定的基本方法是以星敏感器和陀螺作为测量部件，采用卡尔曼滤波算法并结合卫星姿态动力学方程处理传感器测量信息，实现对卫星姿态和陀螺漂移的实时估计[6].

姿态以四元数形式表述，卫星姿态确定系统以姿态运动学方程作为系统方程，用于姿态确定卡尔曼滤波算法设计的姿态误差方程形式如下:

式中，

δq=[δq1，δq2，δq3]T表示卫星定姿误差四元数的矢量部分，δb=[δbx，δby，δbz]T表示陀螺漂移误差，^ω=[^ωx，^ωy，^ωz]T为通过陀螺测量获得的卫星姿态角速率，ng是陀螺的角度随机游走噪声，nb是陀螺角速率随机游走噪声.将星敏感器输出的姿态四元数和四元数估计值之间的误差四元数的矢量部分作为观测量，观测方程可写为

其中，vs表示测量噪声，δqs是根据星敏感器观测量得到的误差四元数的矢量部分.

1.2 ADS测量模型

角位移敏感器(ADS)是基于磁流体动力学(MHD)原理的测量角度的敏感器.磁流体是由强磁性微粒(小于10 nm)均匀地高度弥散于特定液体中而形成的稳定的胶体溶液，既具有液体的流动性，又有固体磁性材料的磁性，拥有许多独特的性质.MHD敏感器的工作原理如下图1所示，一个环形的导电流体置于磁场中，构成敏感器的构架.当敏感器旋转时，流体的惯性会阻碍这种运动，于是就会在固连于敏感器构架的磁场和导电流体间产生相对运动，磁流体和静磁场的相对运动产生电场，进而会在初始线圈中产生电流，经变压器后会在第二个线圈两端产生与角速率输入相关的电位差[7].

图1 磁流体敏感器工作原理

MHD敏感器测得的是运动角速率，ADS是采用3个相互正交的磁流体敏感器和两块电板组成的直接测量角位移的敏感器，其机械配置如图2所示.

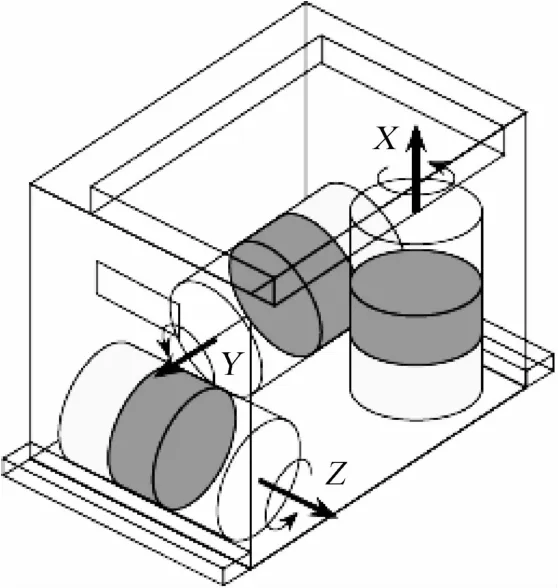
图2 ADS的机械配置

ADS体积小，造价低，持久耐用，精度高(＜0.1 μrad)，对角运动的灵敏度高，测量带宽为2～500Hz，这些特点使其在高频姿态测量中发挥着重要的作用.其测量模型为[3]

其中αi(T)、T)和kk(T)都可表示为的形式.

在高分辨率对地观测卫星中扩展姿态确定带宽的目的是提高有效载荷的指向精度.然而，指向和姿态的相关度会因温度变形引起的低频运动和结构振动引起的高频抖动而降低.为解决这个问题，就要把星敏感器、惯性敏感器和ADS安装在光具座上，光具座、星敏感器支架采用精确的温度控制系统，一方面降低结构变形的影响，另一方面使ADS的测量数据有意义.

1.3 高频姿态抖动模型

导致飞轮出现高频振动的内部因素有很多，主要因素是高速转子产生的不可避免的转子不平衡量.一般可以分为静不平衡和动不平衡两种情况.通过定义幅值系数Ai，可定义由飞轮引起的卫星高频抖动姿态角为[8-9]

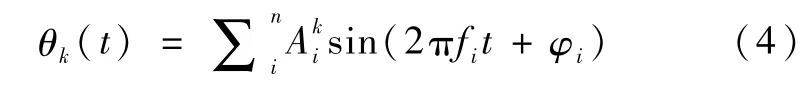
式中，θk(t)为高频抖动姿态角(当k=1，2，3时，分别表示θx，θy和θz)，Ai为第i次谐波的幅值系数，fi为第i次谐波的频率值，φi为第i次谐波的初相位.

2 宽带宽的姿态确定方法

宽带宽姿态确定是分别由低带宽敏感器和宽带宽敏感器测量的姿态信息经过融合滤波器的处理得到宽带宽的姿态信息.由陀螺和星敏感器组成高精度的姿态确定，利用ADS的测量信息扩展姿态确定的带宽，以达到提高有效载荷指向精度的目的.

由陀螺和星敏感器组成的姿态确定系统得到的误差四元数及陀螺漂移估计值对预估的姿态四元数和陀螺漂移进行修正，修正方程为

此时得到的姿态估计为惯性姿态四元数，而ADS的测量输出是本体系内的三轴角位移，因此首先应由惯性姿态四元数推出本体系内的姿态矩阵为

式中，以四元数给出的姿态矩阵的具体形式为

式中，[q ×]为q的反对称矩阵，表示为

由此可得到本体系内的三轴角位移为

将估计得到的角位移按上述相反的过程逆推即可得到姿态四元数.下一节针对三轴的一个轴为例来介绍宽带宽的姿态滤波算法.

3 卡尔曼滤波器的设计

3.1 系统状态方程和量测方程的建立

宽带宽姿态确定系统如图3所示.令x1=θtrue为实际的姿态角，用以下二阶系统描述以星敏+陀螺为姿态测量方式的精确姿态确定系统(PADS)的状态方程和量测方程为

图3 宽带宽姿态确定系统框图

ADS的姿态测量系统的状态方程和量测方程为

考虑状态变量x1，得到整个系统的状态方程和量测方程为

式中，

w(t)是随机系统过程噪声，v(t)是量测噪声，系统噪声和测量噪声是彼此不相关的零均值高斯白噪声，且满足式中q(t)为非负定阵，r(t)为正定阵.

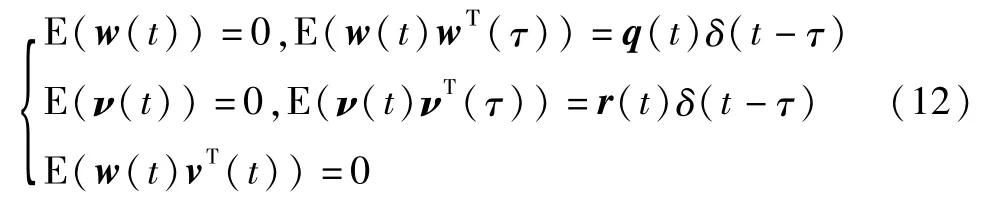
3.2 卡尔曼滤波算法

对式(11)作离散化处理[10-11]，得

式中，Φ(tk+1，tk)为tk时刻至tk+1时刻的一步转移阵，Wk为系统激励噪声序列，H(tk+1)为量测阵，Vk为量测噪声序列.满足方程

式中Δt=tk+1-tk，为滤波周期.

根据对Wk的定义，可得出如下结论

积分变量t∈[tk，tk+Δt)，τ∈[tj+Δt)，而当t≠τ时，δ(t-τ)=0，所以只有当上述两积分区间重合时，积分才不为零，且Δt很小时，q(t)在该区间内可看作常阵，所以

则可得出白噪声序列Wk的协方差阵为

同理可得

Qk和Rk分别为系统噪声和量测噪声的协方差阵，Qk实际是计算模型偏离真实系统模型造成的状态一步预测误差，Rk是计算测量模型偏离真实输出造成的误差，它们确定了滤波器的稳健性和稳态估计精度.

通过时间和测量的更新，得到以下卡尔曼滤波方程，其更新过程如图4所示.

时间更新:

PADS及ADS测量更新:

式中，

图4 卡尔曼滤波更新过程

4 仿真分析

为验证上述基于卡尔曼滤波的宽带宽确定方法的有效性，开展仿真研究.为进行对比，还同时仿真了不融合ADS测量信息的情况.为了保证可比性，两种滤波器采用相同的参数.仿真中的真实姿态角带宽为500Hz，，由陀螺和星敏感器组成的精确姿态确定系统(PADS)采用二阶系统，采样频率为10Hz，ADS测量采用三阶的带通滤波器，采样频率为1kHz，RPADS和RADS分别为PADS和ADS的测量噪声的协方差阵，Q为系统噪声的协方差阵，滤波周期为0.001s.

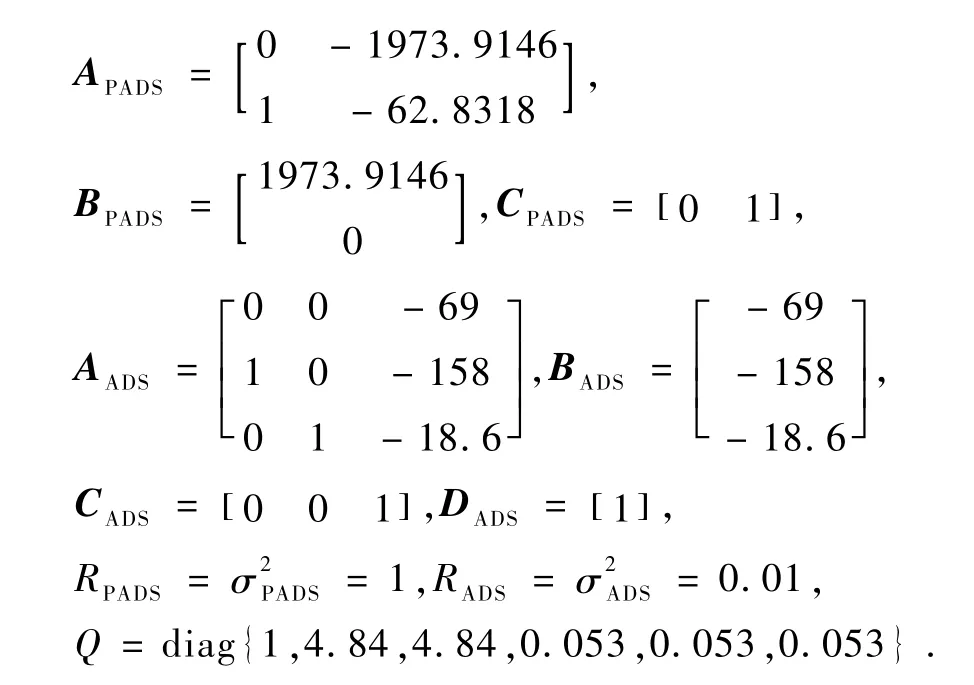
图5为陀螺和ADS的频域响应曲线图，ADS能够测量仅有惯性单元不能测量的高频瞬时姿态运动，由此可得扩展姿态确定带宽的必要性.而由于其磁流体的结构特性，ADS对低频运动不敏感，因此必须结合传统精确姿态确定系统应用，通过滤波器融合算法，提高姿态估计精度.

图5 IRU和ADS频域响应曲线

图6和图7分别为基于卡尔曼滤波的不融合ADS测量信息的和融合ADS测量信息的宽带宽的姿态估计及其误差的仿真曲线.比较图6和图7可以看出，由于高频姿态抖动的存在，使得低带宽姿态测量系统丢失高频姿态测量信息，姿态确定的精度明显比加入高频抖动姿态测量系统的宽带宽姿态确定要低.

图6 精确姿态确定仿真

选择姿态角估计的均方误差E(ε2)来评价姿态确定误差，ε为真实姿态角与估计姿态角的偏差.不融合ADS测量信息的姿态角估计均方误差为0.2739(″)，宽带宽的姿态的姿态角估计均方误差为0.0912(″).

5 结论

本文给出了测量卫星高频姿态抖动以扩展姿态确定带宽的方法，并给出合陀螺、星敏及ADS的姿态确定系统模型，最后用卡尔曼滤波的方法对宽带宽姿态确定系统进行了数学仿真.仿真结果表明，以卡尔曼滤波为基础的融合结果可得到较高的估计精度，说明宽带宽的姿态确定方法可以克服各类传感器测量精度与测量带宽无法兼顾的局限，实现高精度宽带宽的抖动测量，从而可以为平台及载荷指向的在轨闭环控制提供精确的反馈输入.该方法的有效性及良好的效果，为高精度的姿态确定技术提供了有益的参考，具有一定的理论意义.

[1] Iwata T.Precision attitude and orbit control system for the advanced land observing satellite(ALOS)[C].AIAA GNC Conference and Exhibit，Austin，August11-14，2003

[2] Iwata T.Precision attitude and position determination for the advanced land observi-ng satellite(ALOS)[C].SPIE 4thInternational Asis-Pacific Environmental Remote Sensing Symposium，Honolulu，2003

[3] Iwata T.High-bandwidth attitude determina-tion using jitter measurements and optimal filtering[C].AIAA GNC Conference，Chicago，lllinois，August 10-13，2009

[4] Sudey J，Schulman JR.In-orbitmea sure ments of Landsat-4 thematic mapper dynamic disturbances[J].Acta Astronautica，1985(12):485-503

[5] Iwata T.Attitude dynamics and disturbances of the advanced land observing satellite(ALOS):modeling，identification，and mitigation[C].AIAA GNC Conference and Exhibit，Honolulu，Hawaii，August 18-21，2008

[6] 沈莎莎.静止轨道卫星高精度姿态确定方法的研究[D].北京:北京控制工程研究所，2006

[7] Laughlin D，Smith D.Development and perfo-rmance of an angular vibration sensor with 1～1000Hz bandwidth and nanoradian-level noise[C].Free-Space Laser Communication and Laser Imaging，SPIE，2002(4489):208-214

[8] Liu K，Maghami P.Reaction wheel disturbance modeling，jitter analysis，and validation tests for solar dynamics observatory[C].AIAA GNC Conference and Exhibit，Honolulu，Hawaii，August 18-21，2008

[9] 邓瑞清.惯性执行机构干扰特性的研究[D].北京:北京控制工程研究所，2010

[10] Lefferts E J，Markley F L，Shuster M D.Kalman filtering for spacecraft attitude estimation[J].AIAA-82-0070R，5(5):417-429

[11] 秦永元，张洪钺，王淑华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社，1998，33-68

High-Band width Measurement Based Attitude Determination

HE Shimin1，2，TANG Liang1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China;2 Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

According to the high-frequency attitude and pointing jitter that caused by reaction wheel，an angular displacement sensor(ADS)based on the magneto hydrodynamic effect is proposed to measure high-frequency attitude jitter information which conventional attitude sensors can not provide.The technique of attitude estimate based on the extended attitude determination bandwidth is introduced in this paper.The model of the system combined with gyro，star sensor and ADS is built，and the Kalman filter is used to determine satellite attitude.The simulation results indicate that the proposed approach with ADS and high-bandwidth attitude determ ination is better than conventional attitude determination.Accordingly，the validity and accuracy of high-bandwidth attitude determination in satellite attitude determination is verified.

high-frequency attitude jitter;high-bandwidth attitude determination;Kalman filter;angular displacement sensor(ADS)