月球精确软着陆制导轨迹在轨鲁棒跟踪

2011-11-27何英姿刘良栋

空间控制技术与应用 2011年5期

关键词：着陆器制导闭环

梁栋，何英姿，刘良栋

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

月球精确软着陆制导轨迹在轨鲁棒跟踪

梁栋1，2，何英姿1，2，刘良栋1

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

为实现在月球表面期望的着陆点进行精确软着陆(PPL)，在开环制导规划出的最优标称轨迹基础上，考虑动力下降过程中的干扰和不确定性，对在轨闭环轨迹跟踪制导方法进行研究.针对月球PPL三维球体非线性轨道动力学模型，充分考虑自主制导的鲁棒性、实时性要求，采用动态平面控制技术的思想，解决退步法存在的“计算复杂性膨胀”问题，并证明了闭环系统的稳定性.仿真算例表明，该方法不仅算法简单，过渡过程能够实现快速跟踪，而且能够保证稳态跟踪误差在预先给定的范围之内且可以自由调节.

制导;精确软着陆;不确定非线性系统;鲁棒跟踪

为在月球表面具有科学价值的区域进行软着陆探测和取样，希望着陆器能够在一些地形复杂区域安全着陆，这就要求着陆器具有精确软着陆能力;另外，减少着陆器在下降过程中的燃料消耗，对精确软着陆任务来说也是至关重要的.这要求着陆器自主制导单元可以实时规划出最优轨迹，这是一种开环的制导方式.然而在着陆器实际下降过程中，却伴有许多干扰误差源，主要包括初始条件干扰、导航设备测量误差和执行机构误差，此外，还包括月球非球形引力摄动和日、地引力摄动等环境干扰引起的误差.其中，测量误差包括初始导航偏差、惯性装置(IMU)测量误差、LIDAR高度测量误差以及测速雷达等敏感器测量误差;执行机构误差主要来源于制动发动机的推力和姿态误差.因此，着陆器的自主制导控制系统需要有轨迹跟踪控制单元，完成对开环制导单元规划出的最优标称轨迹的跟踪，实现软着陆过程的实时闭环制导.

这就要求设计一种跟踪制导控制律，既对各种干扰和不确定性具有较强的鲁棒性，又能与在轨快速制导相配合，具有较好的实时性.最近几年，国内外有关鲁棒控制的文献针对非线性控制系统提出了多种设计方法.其中退步法是一种应用较为广泛的设计方法[1-3]，其主要思想是在每一步骤，通过选取适当的状态变量作为子系统的虚拟控制输入，设计虚拟控制律达到降低整个系统维数的目的，最后得到真正的反馈控制律，从而实现最终的控制目标.退步法虽然具有很多的优点，但是存在“计算复杂性膨胀”的缺陷，特别是对于系统阶数较高的情况其缺陷尤其显著，由于每一步递推设计中都要对虚拟控制律进行重复求导，导致虚拟控制量所含项随系统阶数的增加以指数形式增长，使得计算项增加，控制律变得高度非线性、高度复杂.对于在轨自主航天器而言，其计算量往往是星载计算机难以承受的.为了克服这一缺陷，国外相关研究进行了一些改进，Swaroop等[4]提出了动态平面控制技术，通过对虚拟控制律进行滤波，避免了求导运算;他们还应用动态平面控制方法研究了非Lipschitz跟踪问题;Yip和Hedrick等[5]对只含线性参数不确定性系统，采用这一方法进行了研究.对于动态平面控制技术，国内也有些应用研究，王中华等[6]将其扩展到更为一般的非线性系统输出跟踪问题，系统同时包含线性参数不确定性和未知非线性函数;周丽等[7]将系统的不确定性及外界干扰由RBF神经网络在线逼近，在现有的自适应神经网络控制器中引入动态面控制技术降低控制的复杂性，同时对参数自适应律进行改进.但目前此类研究在月球精确软着陆制导问题中的应用尚为空白，并不完全适用于软着陆系统模型，对线性参数自适应律的计算仍然存在耗时较长、实时性差的问题.

本文将采用动态平面控制技术的思想，以开环制导单元规划出的最优标称轨迹为期望的参考信号，研究一种适用于在轨制导的鲁棒跟踪简化控制方法，以达到月球精确软着陆制导的要求.

1 不确定非线性系统模型

在考虑干扰和不确定性的情况下，将系统模型写成如下MIMO不确定非自治系统形式:

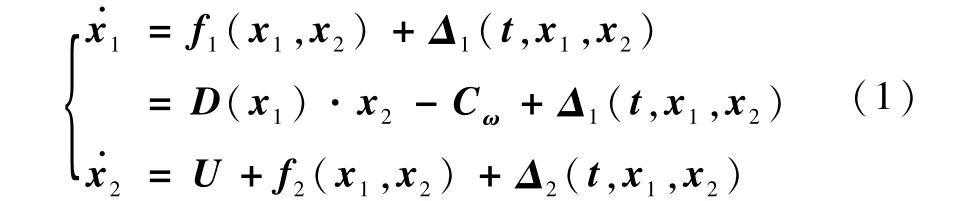
其中，状态向量x1=[rαβ]T∈R3，x2=[u v w]T∈R3;控制输入向量U∈R3;f1(x1，x2)和f2(x1，x2)为光滑函数，Cω=[0ωm0]T为常值项，ωm为月球自转角速度，r为月心到着陆器的距离，α和β表示该月心惯性坐标系下的球坐标经度和纬度，u，v，w分别为着陆器速度在轨道坐标系三轴向上的分量.

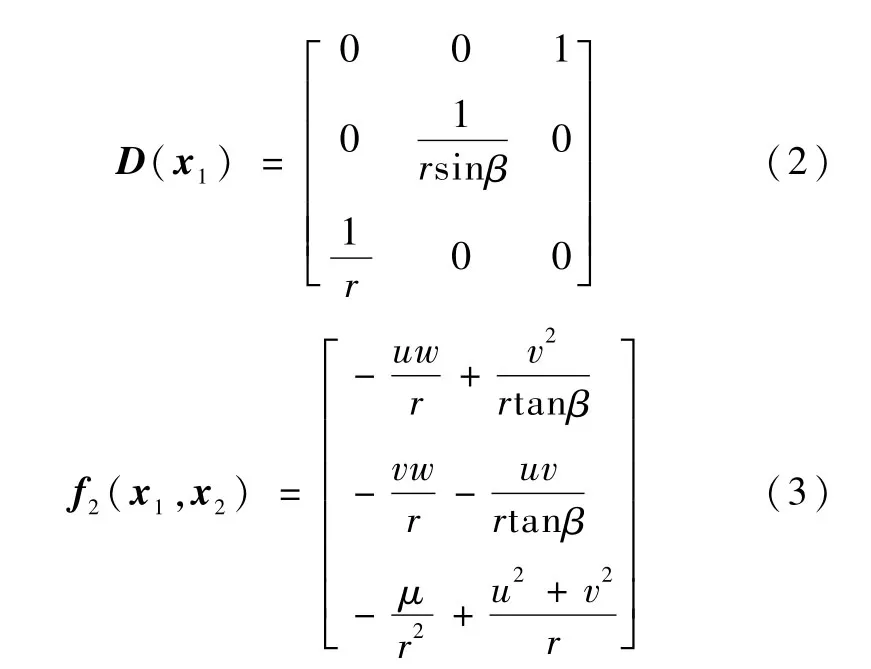
Δi(t，x1，x2)(i=1，2)为未知外界干扰、建模误差及未建模动态的合成项.

针对模型(1)，将规划出的着陆器位置和速度制导轨迹作为参考输入信号，递推设计跟踪控制器.实际中，系统的参考输入和不确定性扰动项满足以下条件:

条件1.对于∀t≥0，参考输入信号2)均有界;

条件2.，其中δi为已知的正常数.

另外，函数D(x1)满足如下假设条件:

条件3.D有界，即存在常数d1≥d0＞0，使得d0≤D≤d1;

条件4.D可逆.

2 基于动态平面的鲁棒控制器设计

控制器设计目标是使得系统状态在预先给定的误差范围内渐进跟踪参考输入信号，并且在算法上简单快速，适于在轨应用.将动态平面控制技术应用于传统的退步法设计过程:

步骤1.考虑闭环系统(1)的第一个子系统

定义误差状态向量S1=x1-x1r，并对其进行求导得

其中，x1r为系统位置参考信号.

选取虚拟控制

其中，k1为设计的常值参数对角矩阵.

引入新的状态变量z2，它是由x2d通过时间常数为τd的一阶滤波器得到的估计值，即

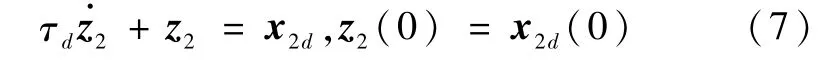
这样就无需在后面步骤设计中对x2d中的非线性项进行求导，从而避免了计算膨胀问题，简化了控制律的运算，提高了实时性.

步骤2.定义第二个误差平面为

对式(8)等号两端进行求导，并将系统(1)第二个方程代入得

设计系统最终的真正控制律为

其中，k2为设计的常值参数对角矩阵.

注1.由退步法的设计过程可以发现，虽然最终的真正控制器是由系统最后一个方程导出，但其中包含第一个子系统的反馈信息，因此可以实现对第一个状态向量x1的跟踪控制;在着陆器软着陆的实际过程中，受到的干扰和不确定性与其对应的状态或状态导数相比，影响比较小，即δi数量级远小于˙xi，这样通过系统方程可以看出，所设计的控制器可以实现位置和速度的全状态跟踪.此点将在后面的仿真中得以体现和验证.

事实上，这也保证了所规划的开环着陆轨迹具有最优性的意义，符合月球摄动、测量误差和推力误差相对较小的实际情况.否则，如果下降过程中扰动对整个系统影响较大，则需要针对新的系统模型重新进行最优标称轨迹的规划.

另外，引入式(7)一阶惯性环节，是对执行机构动态延迟特性在模型上的补偿，更接近实际.

3 系统稳定性分析

为了对所设计的闭环系统进行稳定性分析，首先给出如下的引理:

引理1.考虑如下的Lyapunov函数:

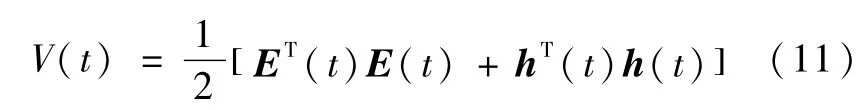
其中，E(t)=x(t)-z(t)，h(t)=z(t)-xd(t)，x(t)∈Rn，z(t)∈Ωz⊂Rn，xd(t)∈Ωd⊂Rn，如果下列不等式成立

其中，a，b为大于零的常数;且z(t)∈Ωz一致有界，则

证明.对式(12)两边在[0 t]上进行积分得

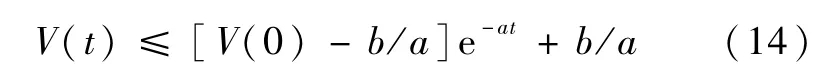
由于函数e-at在区间[0，+∞)上为减函数，故有e-at≤1，则根据式(14)得

结合式(11)，有

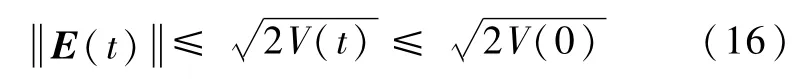
即

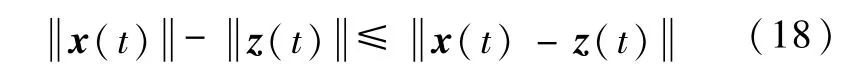
且z(t)一致有界，根据式(17)和式(18)，因此引理1得证.

引理2[8].设V:Rn→R是定义域包含原点的连续正定函数，且V(x)径向无界，则对任意的x∈Rn，存在K∞类函数α1和α2在[0，+∞)上有定义，使得

又

定义系统(1)的边界层误差

对其求导得

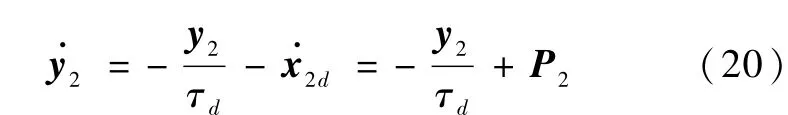
因此闭环系统的误差动态方程为下面给出系统稳定性的定理:

定理1.考虑闭环系统(1)，给定一致有界参考信号x1r，在条件1～4下，采用控制律(10)，任意给定正数p，如果选取闭环系统的初始条件满足

则总存在控制器参数k1、k2和τd，使得闭环系统所有信号一致有界，稳态跟踪误差收敛到原点的一个小邻域内且可以自由调节.

证明.选取系统的Lyapunov函数为

对Lyapunov函数进行求导，并将式(20)和式(21)代入得

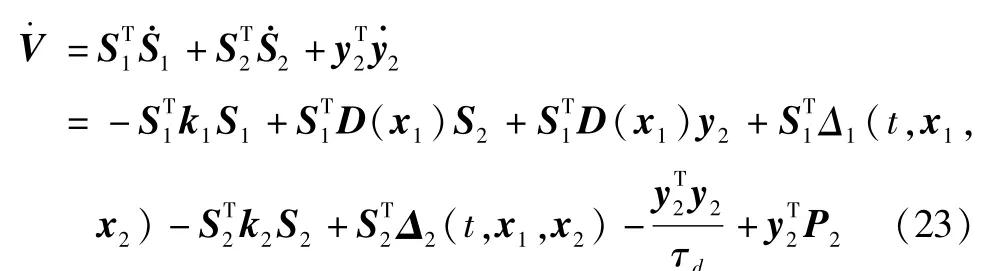
由D≤d1和Δi(t，x1，x2)≤δi，式(23)可以得到如下不等式:

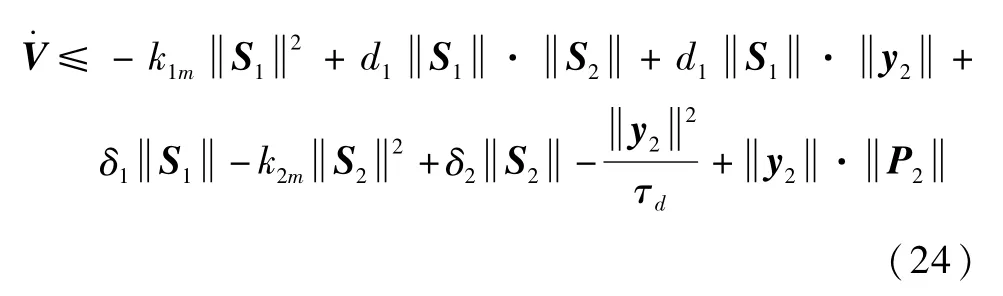
其中，kim为常数矩阵ki的最小特征值.再根据不等式

其中，η为任意正实数，由式(24)有

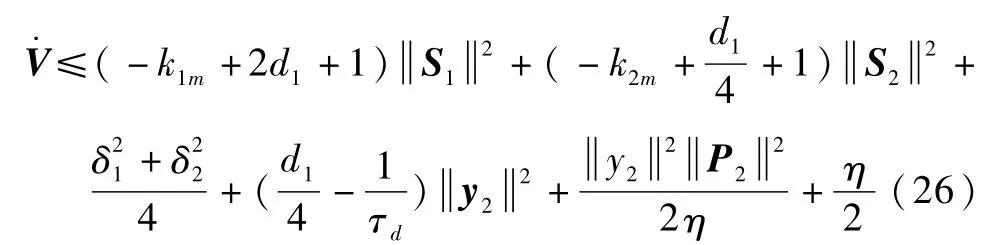
由引理2可知，存在K∞类函数α1和α2，使得

其中，Y是P2的状态向量.

因此，通过加减含K∞类函数项，式(26)可写为

则式(28)可以化为

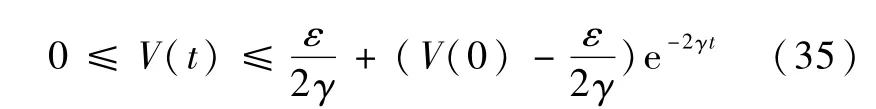
对式(34)求解得由式(35)可知，V(t)一致有界，且R+，存在.再由式(22)可知，S1、S2和y2一致有界.

在式(6)中，因S1一致有界，根据条件1、3和4，知x2d一致有界.再由y2一致有界，和式(19)可知，z2一致有界，由式(7)得，也一致有界.

因此根据引理1，再由条件1及S1=x1-x1r知，x1，x2一致有界.

下面讨论跟踪误差范围的调节问题.对式(28)积分得

可见，式(36)等号左边如果没有干扰带来的常数项，则S1∈L2，S2∈L2，y2∈L2，可由S2一致有界及条件2和式(21)可知，一致有界，因此由S2∈L2∩L∞和∈L∞，运用Barbalat引理可得，当t→∞时，S1→0;再由条件1、2和3及式(21)，且S1、S2和y2一致有界，可知一致有界，因此由S1∈L2∩L∞和∈L∞，运用Barbalat引理可得，当t→∞时，S1→0.但在干扰情况下，无法实现S1→0和S2→0，只能使跟踪误差收敛到原点的一个小邻域内.

4 仿真结果与分析

选取期望参考信号x1r、x2r(如图1～10中虚线)，着陆器初始质量为m0=1500kg，月球引力常数μ=4902.8026km3/s2，发动机比冲ISP=300s.初始误差为

有界干扰未建模动态设为

一阶滤波器时间常数设为τd=0.001;控制器参数设置如下:

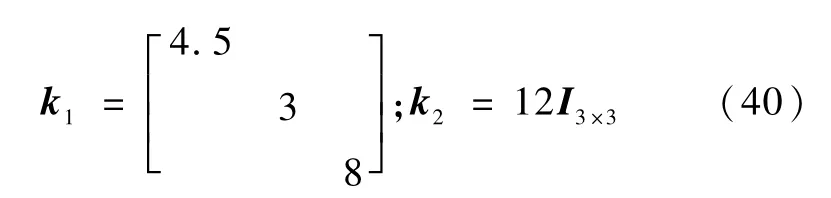
其中，I3×3为3维单位阵.下面给出跟踪结果曲线，如图1～10所示.

由仿真结果可以发现，各路制导参考信号在所设计的控制器作用下都能实现很好的跟踪，特别是三路位置信号，跟踪误差几乎为零;着陆器位置速度的初始误差在几十秒内衰减至较小的可接受范围内，实际信号跟踪上制导参考轨迹，过渡过程过渡过程比较理想，没有出现超调振荡等现象，符合实际要求.由图10的着陆器质量变化曲线可以发现，控制推力抑制初始偏差造成了一定的燃料消耗，实际跟踪结果比目标曲线仅多消耗了16.3728kg燃料，相对于整个软着陆过程来说是很小的.在给定的控制器参数下，跟踪误差可以调节得非常小，因此制导精度高，仿真结果表明了所设计制导控制器的有效性和实用性.

图1 航向速度跟踪结果

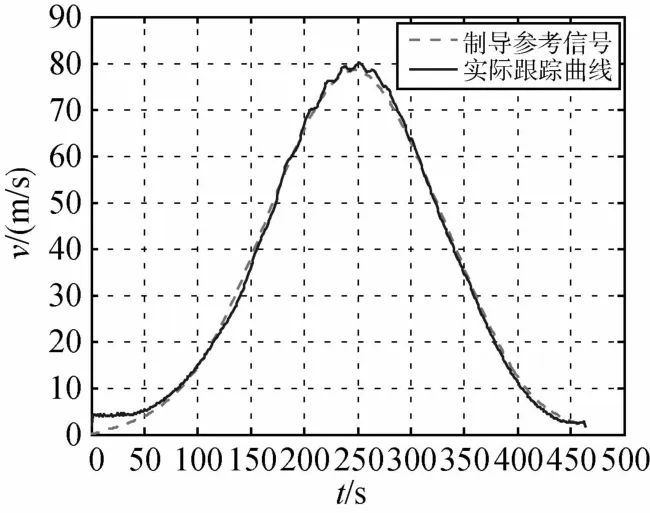
图2 横向速度跟踪结果

图3 径向速度跟踪结果

图4 高度跟踪结果

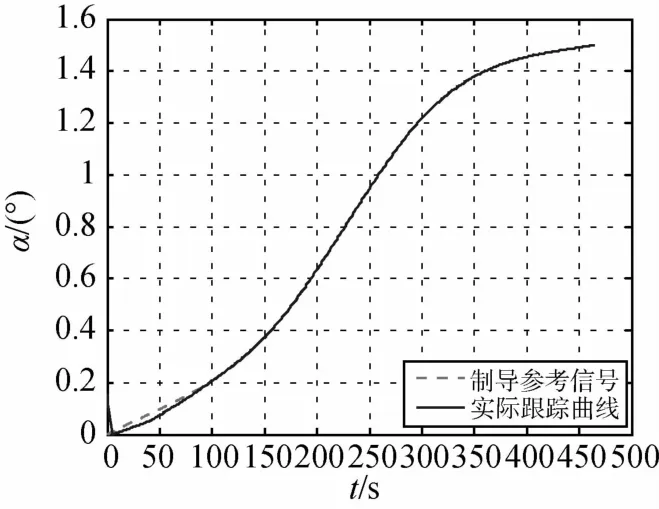
图5 经度跟踪结果

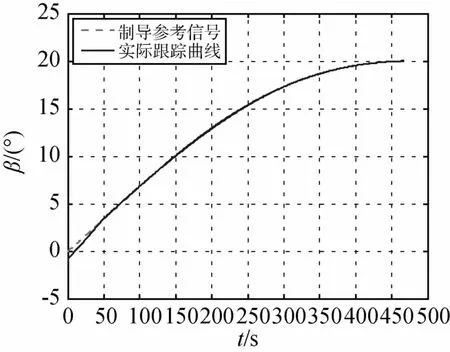
图6 纬度跟踪结果

图7 控制推力跟踪结果

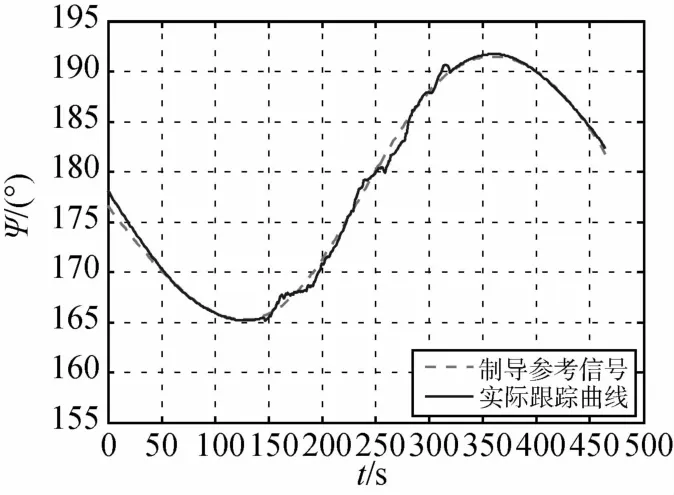
图8 推力角ψ跟踪结果

图9 推力角θ跟踪结果

图10 着陆器质量跟踪结果

5 结论

本文充分考虑初始导航偏差、环境摄动、推力器误差和测量误差等影响，将退步法和动态平面控制技术相结合，针对含干扰和未建模动态的系统设计了闭环鲁棒跟踪控制器，避免了“计算复杂性膨胀”问题，从而使控制律的实施变得更加简化，并证明了闭环系统的稳定性.对各路信号理想的跟踪结果也验证了该方法的有效性.本文的研究对今后深空探测工程中在轨实时跟踪最优标称轨迹的制导方案具有参考和实用价值.

[1] Krstic M，Kanellako poulos I，Kotovic P V.Nonlinear and adaptive control design[M].New York:W iley，1995

[2] Yao B，To mizuka M.Adaptive robust control of SISO nonlinear systems in semi-strict feedback form[J].Automatica，1997，33(5):893-900

[3] Ge S S，Hong F，Lee T H.Robustad aptive control for a class of perturbed strict-feedback nonlinear systems[C].American Control Conf.，Boston，Massachusetts，2004

[4] Swaroop D，Gerdes JC，Yip P P，et al.Dynamic surface control for a class of nonlinear systems[C].American Control Conf.，Albuquerque，NM，1997

[5] Yip P P，Hedrick J K.Adaptive dynamic surface control:a simplified algorithm for adaptive back stepping control of nonlinear systems[J].Int.J.Control，1998，71(5):959-979

[6] 王中华，程林，张勇.不确定非线性系统的鲁棒自适应跟踪简化算法[J].系统工程与电子技术，2007，29(3):412-415

[7] 周丽，姜长生.改进的非线性鲁棒自适应动态面控制[J].控制与决策，2008，23(8):938-943

[8] Khalil H K.Nonlinear systems(third edition)[M].Beijing:Publishing House of Electronics Industry，2005

On-Board Robust Tracking of Guidance Trajectory for Lunar Pinpoint Soft Landing

LIANG Dong1，2，HE Yingzi1，2，LIU Liangdong1
(1.Beijing Institute of Control Engineering，Beijing 100190，China;
2.Science and Technology on Space Intelligent Control Laboratoy，Beijing 100190，China)

Considering disturbances and uncertainties，a closed-loop guidance system is designed on the basis of optimal nominal trajectory generated by open loop guidance law.From the point of view of real time performance，the dynamic surface control(DSC)technique is used to overcome the‘explosion of computation complexity 'problem of the traditional back stepping method.The designed robust tracking guidance law for the uncertain nonlinear system with modeling errors and external disturbances is simpler than the existing algorithms based on the traditional back stepping method.It is theoretically proved by using the Lyapunov stability theory that the closed-loop system is uniformly bounded.And the steady tracking errors stay in the prescribed bound.The performance and effectiveness of the proposed synthesized closed-loop nonlinear guidance system are verified by numerical simulation results.

guidance;lunar pinpoint soft landing;uncertain nonlinear system;robust tracking