极大代数上线性系统的3维最小实现的研究

张 静, 张仁忠

(通化师范学院数学系,吉林通化 134002)

极大代数上线性系统的3维最小实现的研究

张 静, 张仁忠

(通化师范学院数学系,吉林通化 134002)

研究了极大代数上线性系统的3维最小实现问题,给出了特征方程为λ3⊕c0λ0=c2λ2⊕c1λ,当c1=,c0=c1c2时,无穷序列存在3维最小实现的充要条件.

极大代数;最小实现;周期序列

1 引 言

(1.2)称为(1.1)的一个实现,(1.1)称为可实现序列.若(1.2)的维数均小于或等于(1.1)中任意一个实现的维数,则(1.2)称为(1.1)的最小实现,且A的阶数称为最小实现的维数.

求最小实现问题是线性系统研究中的一个困难问题,近20年来,国内外许多学者对该问题做了研究,并取得了一系列成果.但寻找存在n维最小实现的充要条件这一问题尚未得到解决,文[1]曾在这方面做了重要探索,给出了一个充要条件,由于至今没有给出该条件的严密证明,将其称为涂奉生猜想.

涂奉生猜想[1]无穷序列0∞存在n维最小实现的充分必要条件为它是一个n阶周期序列.

文[2]给出了存在1维与2维最小实现的充要条件,彻底解决了1维与2维最小实现问题,并说明了涂奉生猜想在小于等于2维的情况下成立,但在大于2维的情况下不成立.文[3]研究了几类3阶周期序列的3维最小实现问题,得到了大部分3阶周期序列存在3维最小实现的充要条件.

本文研究了文[3]未解决的特征方程为λ3⊕c0λ0=c2λ2⊕c1λ,当c1=,c0=c1c2时,序列存在3维最小实现的充要条件问题.

2 准备工作

定义2.1[4]设A为极大代数上n×n矩阵,对于λ≠ε,若存在向量X,使得AX=λX,则称λ为A的一个特征值,X称为特征向量,A的特征方程定义为

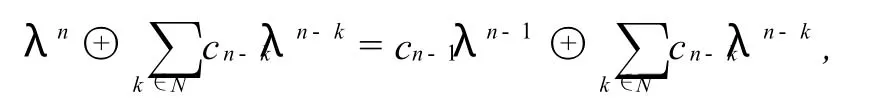
其中N∪￣N={2,3,…,n},N∩￣N=Ø,系数cn-k的图论解释如下:

设矩阵A对应的有向图为G(A),在图G(A)中由一个或几个回路组成的总长度为k的回路的集合,且回路集合的结点数和弧数相同,则称这个回路集合为k阶回路集.若k阶回路集中所含回路的个数为偶数ei(i∈0∪N,其中N为自然数的全体),则记回路集的权重为W(ei,k);若k阶回路集中所含回路的个数为奇数oi(i∈0∪N),则记回路集的权重为W(oi,k).对于∀v∈R,记Ne=‖{i;W(ei,k)=v}‖No=‖{i;W(oi,k)=v}‖,则cn-k=max{v,Ne≠No},其中若Ne＞No,则k∈N;若Ne＜No,则k∈

3 主要结果

证必要性.c0为一个2阶单回路和一个自回路的权重之和,c1为一个2阶单回路的权重,c2为一个自回路的权重.由c1=c22知c1为一权重最大的2阶单回路的权重,c2当然为权重最大的自回路的权重.又由c0=c1c2知权重为c1的某2阶单回路与某个权重为c2的自回路没有公共端点.(当有一个c时,某c1与c2无公共端点,当有两个c2时,至少有两个c1,但不可能有三个c2.)

一、若c′1=c1,分两种情况讨论,在置换的意义下简图如图1.

(A)若g0=b2d2⊕b3d3,则gk+3≥c′1c2gk=c0gk,k=0,1,2,…由序列满足gk+3⊕c0gk=c2gk+2⊕c1gk+1,k=0,1,2,…,知序列元素之间的关系为gk+3= c2gk+2⊕c1gk+1,k=0,1,2,…,即情况①.

(B)若g0=b1d1.

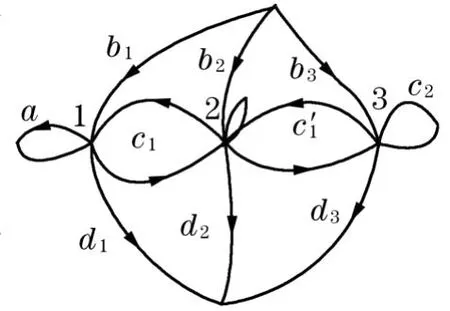
图1

(A)若a=c2,则存在另一个权为c1的2阶单回路,在置换的意义下简图如图2,则由图可知gk+3≥c1c2gk=c0gk,k=0,1,2,…由序列满足gk+3⊕c0gk=c2gk+2⊕c1gk+1,k=0,1,2,…,知序列元素之间的关系为gk+3=c2gk+2⊕c1gk+1,k=0,1,2,…,即情况①.

(B)若a＜c2,简图如图1.

(i)若g0=b1d1(同法可证g0=b2d2的情况),则有g1≥ag0,g2≥c1g0.

(a)若g1=ag0,则g3≥c1g1.

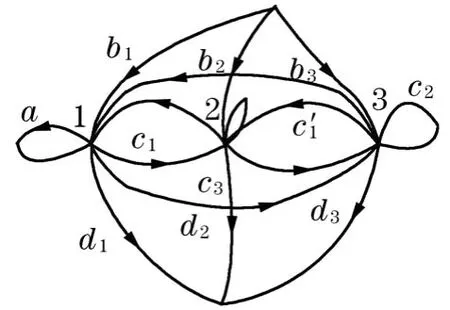
图2

4 结束语

本文以矩阵对应的有向图为工具,结合cn-k的图论解释,给出了特征方程为λ3⊕c0λ0=c2λ2⊕c1λ,当系数c1=,c0=c1c2时,无穷序列存在3维最小实现的充要条件,进一步解决了存在3维最小实现的充要条件问题.

[1] 涂奉生.极大代数上线性系统的最小实现[C]∥1992中国控制与决策学术年会论文集.哈尔滨：《控制与决策》编辑部,1992：184-189.

[2] 孙志敏,陈文德,于洪年.极大代数上线性系统的最小实现[J].控制与决策,2006,21(5)：521-526.

[3] 孙志敏,陈文德.极大代数上线性系统的3维最小实现[J].系统科学与数学,2007,27(4)：499-509.

[4] Blondel V D,Portier N.The minimal realization problem in the max-plus semiring and pisot’s problem are NP-hard [J].C.R.Acad.Sci.Paris,t,333,SérieI.2001：1127-1130.

On 3-dimensional Minimal Realization in Linear System of Max-algebra

Z HA N G J ing, Z HA N G Ren-zhong
(Department of Mathematics,Tonghua Normal College,Tonghua,Jilin 134002,China)

The 3-dimensional minimal realization of linear system in the max-algebra is studied.The necessary and sufficient condition for the existence of 3-dimensional minimal realization of the infinite sequenceis given,that the characteristic equation of the infinite sequence isλ3⊕c0λ0=c2λ2⊕c1λ,wherec1=,c0=c1c2.

max-algebra;minimal realization;periodic sequence

O231

A

1672-1454(2011)03-0030-06

2008-08-01;[修改日期]2008-11-27

吉教科验字[2007]34号