二维连续型随机变量相关计算的积分限确定问题

吕洪升, 张千祥

(巢湖学院数学系,安徽巢湖 238000)

二维连续型随机变量相关计算的积分限确定问题

吕洪升, 张千祥

(巢湖学院数学系,安徽巢湖 238000)

对二维连续型随机变量的积分定限问题进行了简要的归纳和总结,并给出了几类常见计算的基本方法和技巧,以期对学生的积分计算有所帮助.

随机变量;分布函数;密度函数;联合分布;边缘分布

公共概率论与数理统计学习中,在一维随机变量的基础上,二维随机变量的概念顺理成章,易于理解和掌握.但二维连续型随机变量的分布函数、边缘分布密度和随机变量函数密度的计算所涉及的积分问题却令人头痛,尤其是积分区间的确定更让人作难,不仅费时费力,还难以准确求出.而教材或辅导材料上都是针对具体问题给出计算方法和技巧,很少有较系统、全面的方法归纳和总结,若遇到新的问题还是难以下手.本文根据自己几十年的概率教学经验,对这类计算问题作一简要归纳,供学生学习时参考.

1 已知随机变量(X,Y)的联合密度函数,求Z=g(X,Y)的分布密度

这类计算由于函数Z=g(X,Y)(假设为连续)的结构不同有各种不同方法,但所有方法都源于分布函数的定义,即先求出随机变量Z=g(X,Y)的分布函数FZ(z),再求导获得密度函数fZ(z),问题归结为如何求出分布函数FZ(z),现具体讨论如下:

设(X,Y)的联合密度函数为f(x,y),则Z=g(X,Y)的分布函数为

对于这个公式,抽象分析一下,可分为两步完成计算:

第一步,先求出α=min{g(x,y)},β=max{g(x,y)},(这里可能有α=-∞,β=+∞).当z＜α时, FZ(z)=0;z＞β时,FZ(z)=1.因此fZ(z)=0.

第二步,再求FZ(z)在区间[α,β]中的值.这一步是问题关键,不论函数z=g(X,Y)结构如何,其计算方法都是根据z在[α,β]中的不同值确定积分区域D={(x,y)|g(x,y)≤z}与f(x,y)＞0的区域公共部分,这一点明确了,积分计算是轻而易举的事.密度函数fZ(z)也只要对函数FZ(z)求导就能轻松获得.

函数Z=g(X,Y)类型很多,但常见的是和差与积商,下面对和函数Z=X+Y的密度的求法进行讨论(Z=g(X,Y)其它形式也大同小异,大家可据此举一反三).

根据分布函数的定义,Z=X+Y的分布函数为

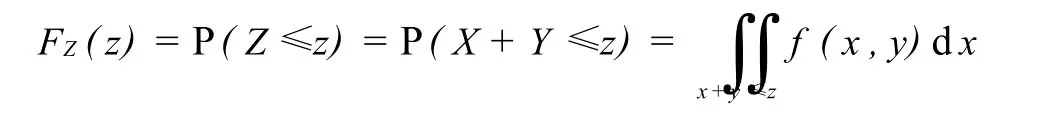
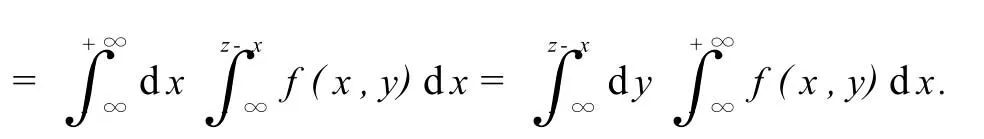
以

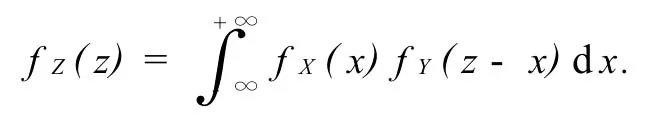
再由X,Y的对称性,得到Z=X+Y的密度计算公式[1]:

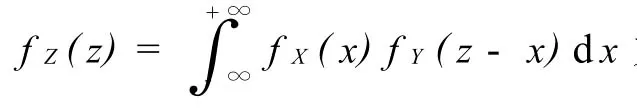
第一步,由于g(x,y)=x+y,所以α=m in{g(x,y)∈(a,b)×(c,d)}=a+c,β=min{g(x,y)∈(a,b)×(c,d)}=b+d(当然对这个具体问题,当z-c＜a或z-d＞b时,两个区间不相交,由此可更清楚地看到结论),当z＜a+c或z＞b+d时,fZ(z)=0.

第二步是关键,又可分以下三步来完成:

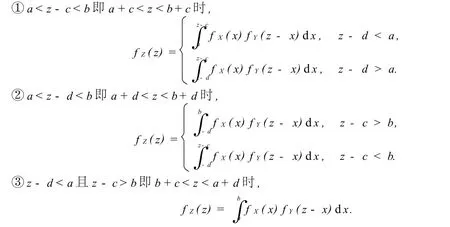
这里是对和函数的一般讨论,显得较烦琐,具体问题要方便得多.下面看一个实例.

例1 在一简单电路中,两电阻R1和R2串联连接,设R1,R2相互独立,概率密度都为

求总电阻R=R1+R2的概率密度[1].

分析 由于R1,R2相互独立,(R1,R2)的联合密度容易求出,R=R1+R2的分布密度有多种求法,如果选择得当,可以大大减轻计算量.下面以多种方法求之.

方法一[1].用卷积公式直接求R的密度fR(z).

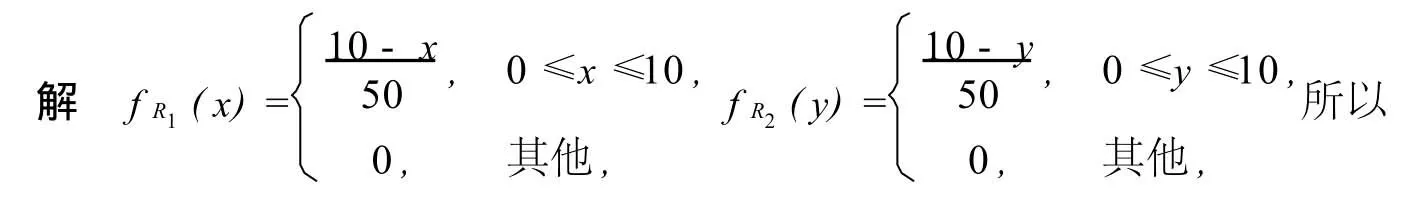
方法二.也用卷积公式,先利用不含参数z的函数fR1(x)确定积分限,再根据参数z的值讨论被积函数的表达式.

②α≤z≤β即0≤z≤20时,(X,Y)联合密度的正值区域D与积分区域M={(x,y)|x+y≤z}的公共部分为G(图1,图2中的阴影部分).

当0≤z≤10时(图1),

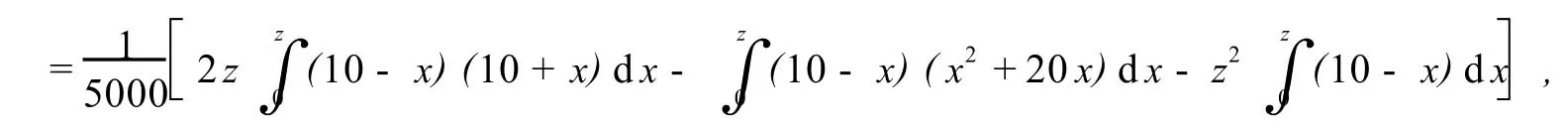
图1

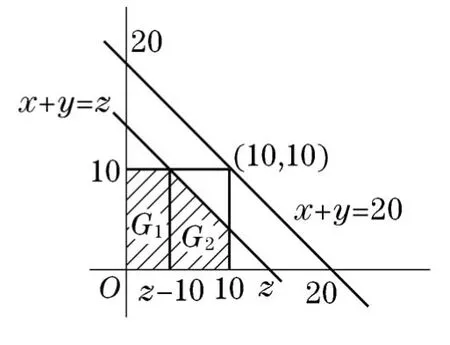
图2

当10＜z≤20时,(X,Y)的联合密度正值区域D与积分区域M={(x,y)|x+y≤z}的公共区域分为G1和G2两个部分(图2),且

综合即得(1)式.

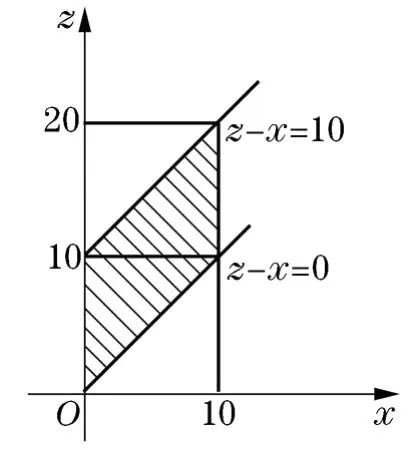
图3

2 已知(X,Y)的联合密度f(x,y),求两个边缘分布密度

其公式是

就前一个公式而言,这类计算是视x为参数,对参数x不同值,确定正密度区间再直接积分就能求出,看下面的例子.

例2 设区域D由直线y=x+1,x=0,y=0围成,随机变量(X,Y)服从D上的均匀分布,求两个边缘分布密度fX(x),fY(y).

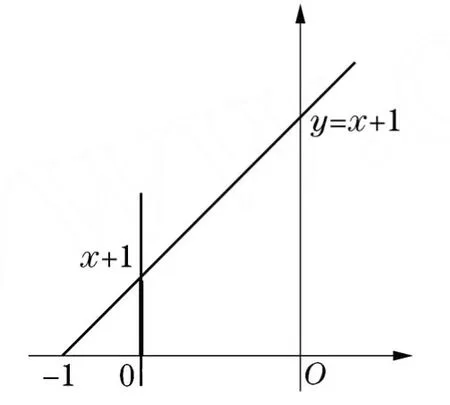
图4

图5

解 (X,Y)服从D上的均匀分布,联合密度为

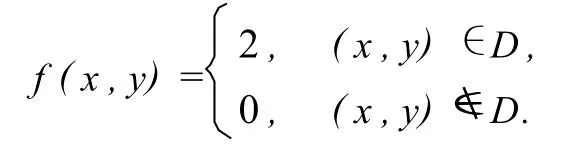
当且仅当-1＜x＜0时,被积函数f(x,y)＞0的区间为(0,x+1)(图4的黑粗线部分),所以当-1＜x＜0时,

3 已知(X,Y)的联合密度,求联合分布函数F(x,y)

其公式是[2]

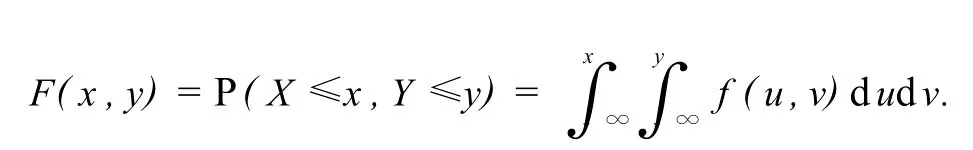
从公式我们看到,这类计算只要能够根据联合密度的正值区域D与广义矩形(-∞,x]×(-∞,y]的交集情况确定联合分布函数F(x,y)表达式的区域划分,余下的积分计算将是水到渠成的事.尽管如此,上述交集情况复杂,且没有通用的区域划分方法,只能具体问题具体对待.下面的例子给出了分布函数F(x,y)的一般求法.

解 根据联合密度的正值区域特点,(X,Y)的分布函数F(x,y)可分为三个表达式,相应平面划分为三个区域D={(x,y)|0≤y≤x},G1={(x,y)|x＜0或y＜0}和G2={(x,y)|0≤x＜y},其中区域D为联合密度函数的正值区域(如图6).

图8

图7

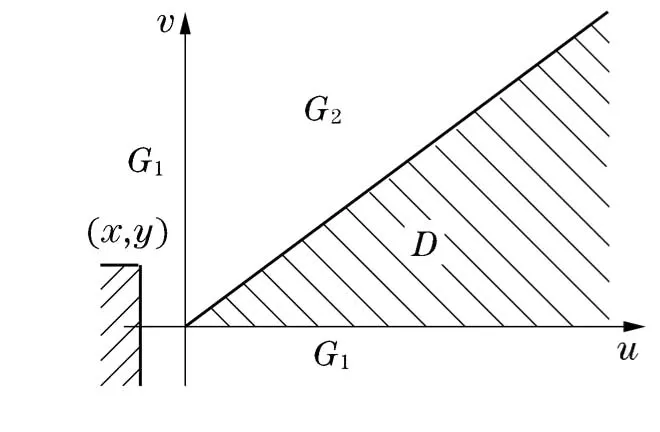
图6

当(x,y)∈G1时,广义矩形(-∞,x]×(-∞,y]与联合密度函数的正值区域D不相交(图6),所以F(x,y)=0.

当(x,y)∈G2时,广义矩形(-∞,x]×(-∞,y]与联合密度函数的正值区域D交集设为D1(图7中的黑粗线内区域),所以

[1] 盛骤,等.概率论与数理统计[M].北京：高等教育出版社,2001.

[2] 魏宗舒,等.概率论与数理统计教程[M].北京：高等教育出版社,1983.

On Calculating the In tegration Problem for Two Dimensional Continuous Random Variables

LV Hong-sheng, ZHANGQian-xiang
(Department of Mathematics,Chaohu College,Chaohu,Anhui 238000,China)

This paper summarizes the two dimensional definite integration p roblem of random variables,and p rovides several commonly used meethods and technology to solve those p roblems in o rder to help the students in calculation.

random variables;distribution function;density function;marginal distribution;definite

O211.1

C

1672-1454(2011)03-0194-06

2009-08-17;[修改日期]2009-12-28

安徽省教育厅质量工程教研项目(20100967)