永磁偏置轴向磁轴承的磁悬浮机理与有限元分析

赵旭升，邓智泉

(1.南京航空航天大学，江苏南京210016;2.南京化工职业技术学院，江苏南京210048)

0 引 言

伴随着能源危机的加剧，世界各国对风力发电等绿色能源技术及飞轮储能等新型储能技术都越来越重视，这就为磁轴承技术开辟了新的应用领域。但实际运行的风力发电及飞轮储能装置，对轴承功耗有一定的要求，飞轮轴承损耗功率小于电机功率的3%以下才有工程实用价值［1］。为了降低轴承功耗，使磁轴承能够在实际中得以应用，则需广泛使用不产生功耗的永磁磁力轴承，但永磁轴承在6个自由度方向至少存在1个自由度方向不稳定，所以它不能单独用于支承转子，而必须与其它轴承(如电磁轴承、超导磁轴承或机械轴承)联合使用［2］，这就为研究低功耗轴向磁轴承提供了广泛的应用前景。永磁偏置磁轴承利用永久磁铁产生的磁场取代主动磁悬浮轴承中电磁铁产生的静态偏置磁场，具有功耗低、电磁铁匝数少、轴承体积小等优点，在飞轮储能、涡轮分子泵等高速应用场合具有广阔的应用前景［3－8］。本文在文献［8］的基础上研究了一种永磁轴向偏置磁轴承，其结构较为简单，控制方便，悬浮转子铁心为薄片状圆盘分置于轴向定子的两侧，轴向磁路与径向磁路完全解耦，控制方便，适用于高速、低功耗的场合。

1 永磁偏置轴向磁轴承的结构及其工作原理

1.1 永磁偏置轴向磁轴承的结构

永磁偏置轴向磁轴承结构图如图1所示，其由轴向定子磁极、轴向控制绕组、径向定子、径向充磁的环形永磁体、转子铁心等构成。其中，轴向定子磁极为实心软磁材料制成，轴向定子磁极上绕有轴向控制绕组。径向充磁的环形永磁体采用钕铁硼制成，嵌装在轴向定子中。为了便于高速运行，两个转子铁心也用实心软磁材料制成薄片圆盘状套装在转轴上，分置于轴向定子的两侧，与轴向定子形成轴向气隙。

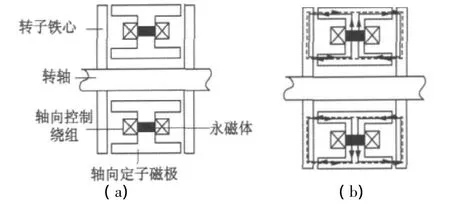
图1 永磁偏置轴向磁轴承结构

1.2 永磁偏置轴向磁轴承的工作原理

永磁偏置轴向磁轴承的磁路图如图1所示。环形永磁体产生偏置磁场(图1中实线所示)，经轴向定子磁极、轴向气隙、转子铁心形成闭合磁路。轴向控制磁通在轴向定子磁极、轴向气隙、转子铁心形成闭合回路，如图1中虚线所示。从磁路图可见，偏置磁通和控制磁通只在轴向流通，与径向完全解耦;轴向悬浮力有内外两个磁极共同产生，单个轴向磁极的面积得以减小，则位于轴向定子磁极两侧的转子铁心可制成薄片圆盘状，只需保证磁密不超过软磁材料的饱和值。这种圆盘状的转子铁心不但缩短了磁轴承的轴向长度，提高了转子的临界转速，同时也缩短了轴向磁通的磁路，降低了轴向励磁磁通的损耗。

轴向自由度的基本工作原理如下:当转子位于轴向平衡位置时，由于结构的对称性，环形永磁体产生的偏置磁通在转子铁心内外两个轴向端面的右面气隙和左面气隙处是分别相等的，此时左右吸力相等。假定此时转子向左偏移一微小位移，则轴向控制绕组通以控制电流在轴向气隙中产生控制磁通与偏置磁通叠加，右端面的内外两个气隙中磁场增强，左端面的内外两个气隙中磁场减弱，在转子铁心上产生水平向右的悬浮力。若转子受到向右的扰动力，则控制电流反向，形成的控制磁通反向与偏置磁通叠加，形成向左的悬浮力。

2 永磁偏置轴向磁轴承的数学模型

2.1 等效磁路分析

为了简化磁路图，做如下假设:考虑磁路不饱和，由一个径向充磁的永磁体提供偏置磁通，考虑工作气隙的磁阻，忽略铁心磁阻、转子磁阻及涡流损耗等，可得到如图2所示的磁轴承等效磁路图。

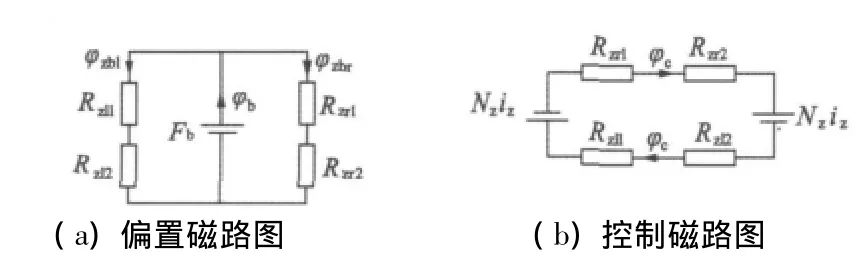
图2 永磁偏置轴向磁轴承等效磁路图

图2中，Fb为永磁体对外提供的磁动势，φb为偏置磁通，Nziz为控制磁动势，φc为控制磁通，Rz为轴向气隙磁阻。

现假设转子铁心轴向向左偏移z，则有:

式中:μ0为空气磁导率;gz为轴向气隙长度;Sz为轴向定子磁极面积。由于结构上的原因，该型磁轴承的控制磁通在内外两个气隙处的漏磁相差较大，如果内外两个磁极面积相等，则内外两个气隙处的控制磁密相差较大，需根据控制磁通的漏磁来调整分配内外磁极面积，即:

同时，欲保证内外气隙偏置磁密的大小相等，还需调整永磁体在轴向定子中的位置，即改变偏置磁通的大小，使内外轴向气隙的偏置漏磁系数满足:

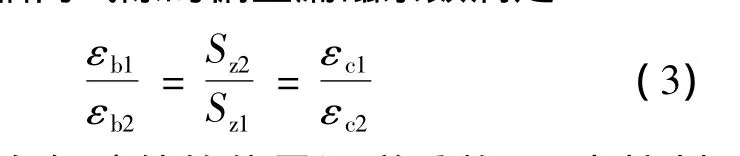
式中:εb为轴向气隙处的偏置漏磁系数;εc为控制磁通在气隙处的漏磁系数。

根据磁路图并利用磁路基尔霍夫定律可求出气隙下的偏置磁通:

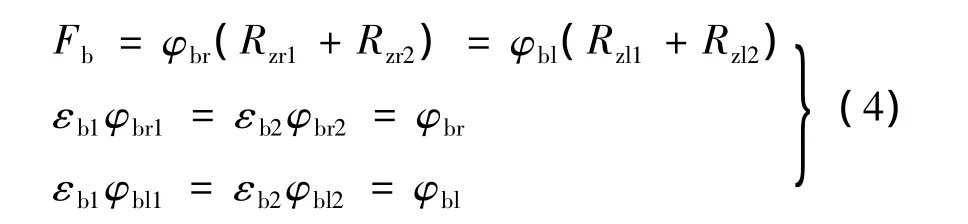
同理可求出控制磁通:

2.2 轴向磁悬浮力方程

由于转子轴向向左偏移z，要使转子回到轴向平衡位置，则需要轴向气隙处的合成磁通产生的合力向右，根据磁场力与磁通的关系，有:

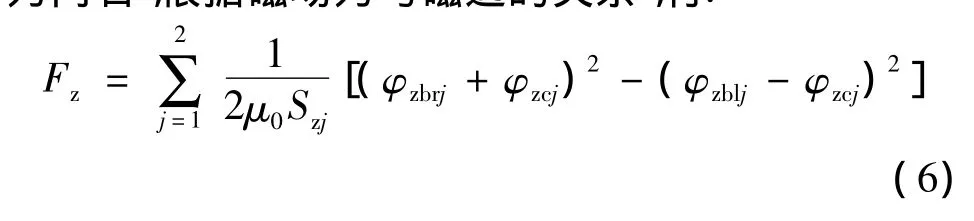
将式(2)～式(5)的值代入到式(6)中，并对Fz在平衡位置附近进行线性化处理并略去二阶以上无穷小量得:

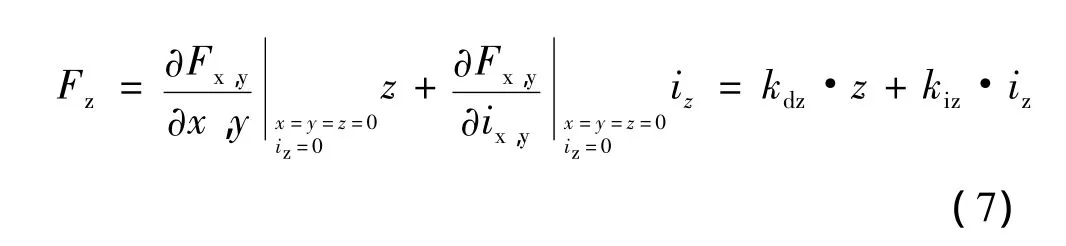
式中:kdz为轴向力/位移系数，

kiz为轴向力/电流系数，

3 永磁偏置轴向磁轴承的参数设计

3.1 轴向气隙磁通密度的确定

在此取气隙偏置磁密Bzb=0.8 T，稍大于软磁材料饱和磁通密度的一半，以增加永磁材料充磁方向的厚度，主要是考虑到永磁材料的精加工难度较大，若充磁方向厚度太小，其能容许的加工误差也会比较小。气隙中控制磁场的磁通密度设定为Bzc=0.4 T，稍小于软磁材料饱和磁通密度的一半，降低气隙中控制磁场的磁通密度可以减少控制绕组的匝数，从而降低控制绕组电阻的功率损耗。

3.2 轴向定子磁极面积的确定

由式(6)可得出轴向悬浮力:

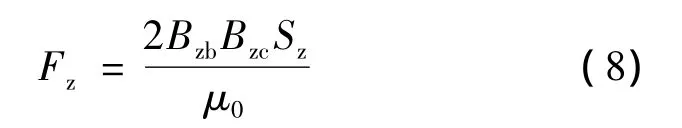
根据所需轴向悬浮力的大小及所确定的气隙中偏置磁密及控制磁密的大小，可求出相应的轴向磁极面积。

3.3 轴向控制磁场及控制线圈

利用求得的磁极面积和设定的气隙控制磁密可求出气隙控制磁通φzc，再利用式(5)，可求得控制线圈的安匝数:

fc为控制磁路的磁阻系数，明确气隙长度gz(0.15～1.0mm)，可得轴向控制绕组的安匝数，由导线电流密度(4～6 A/mm2)选取相应导线，确定出控制绕组的面积:

式中:dm为导线直径(包括绝缘层厚度)。

根据求得的控制绕组的面积可求出控制绕组的径向高度hp:

式中:γ为绕组排列系数(0.6～0.8);ta为绕组的轴向长度。

3.4 定转子各结构参数的设计

为便于安装及减小与转轴间的漏磁，取轴向定子与转轴间隙为5倍的气隙长度，则有轴向定子下磁极高度hi:

式中:ri为转轴半径。

轴向定子上磁极高度ho:

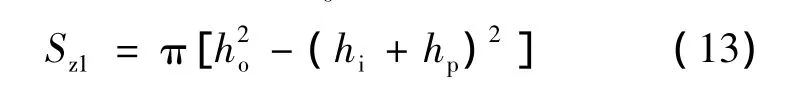
转子铁心圆盘的半径rj:

为避免软磁材料饱和，取转子铁心圆盘的轴向长度rL等于内轴向定子磁极的径向高度:

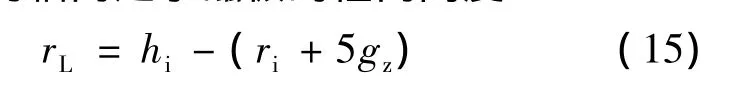
3.5 偏置磁路的参数设计

结合图2，可得永磁体对外提供的磁通:

3.6 永磁体参数的设计

采用径向充磁的环形永磁体的结构参数包括内径Dmgi、径向充磁厚度Tmg及轴向长度Lmg。根据磁轴承的几何关系，永磁环内径等于径向定子圆盘外径。永磁材料选用烧结钕铁硼，Hc为矫顽力，Br为剩余磁密，其退磁曲线接近直线，可表示:

式中:μp为永磁体的磁导率为永磁体工作点参数。

但在工程实践中，永磁体沿充磁方向的厚度受到工艺水平、性价比等客观条件的限制，因此在设计时可将永磁环的径向厚度设置为确定值，其数值的选择应尽量使计算出的永磁体工作点位于其最大磁能积点附近。从图2可得:

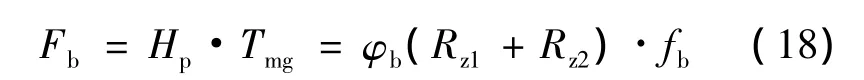
式中:fb为偏置磁路的磁阻系数。

根据求得的永磁体工作点处的磁场强度Hp，再结合永磁体的磁化曲线，可求得工作点处的磁密Bp大小，求得永磁体的中性面面积:

根据几何关系，可得永磁环轴向长度:

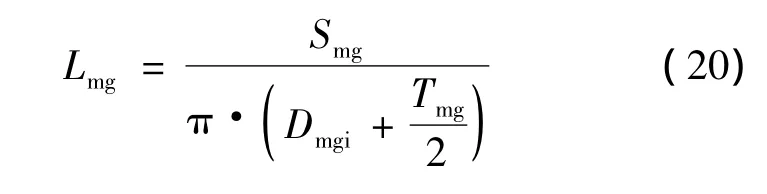
根据几何关系，永磁环轴向长度不应大于轴向定子的轴向长度。同时，为满足式(3)，还需对永磁体在轴向定子的位置作相应调整。

4 设计结果与有限元仿真

4.1 设计要求和设计结果

表1给出了承载力的设计要求、转轴尺寸及其它设计参数，利用上述一系列公式可求出磁轴承参数。

表1 设计要求和已知参数

表2给出了根据上述一系列公式求得的磁轴承参数。

表2 设计结果

4.2 气隙磁场的有限元仿真

由于该型磁轴承的磁通都在轴向流通，可利用有限元分析软件Ansoft对设计结果进行了二维轴对称场仿真分析，以验证永磁偏置轴向磁轴承结构设计的合理性和参数设计的正确性。分析了轴向控制磁通的磁力线分布及磁密大小，偏置磁通的磁力线分布及磁密大小，偏置磁通和控制磁通共同作用时的磁力线分布、磁密大小及转子受力情况。

图3a为控制磁场磁力线图及磁密图，轴向内外气隙中磁通密度都接近0.4 T，符合设计要求。此时，上气隙漏磁系数εc1=1.81，下气隙漏磁系数εc2=1.27，控制磁路的磁阻系数fc=1.02。

图3b为偏置磁场磁力线图及磁密图，轴向气隙中偏置磁场磁通密度接近0.8 T，符合设计要求。此时，上气隙漏磁系数εc1=1.74，下气隙漏磁系数εb2=1.22，所得到的结果满足式(3)。通过有限元仿真最终确定偏置磁路的磁阻系数为1.05。

偏置磁场和控制磁场共同作用时的磁力线图及磁密图如图3c所示，此时加以轴向激励为最大电流2 A，合成磁密左侧约为0.41 T，右侧约为1.19 T，转子铁心的合力为790.3 N。

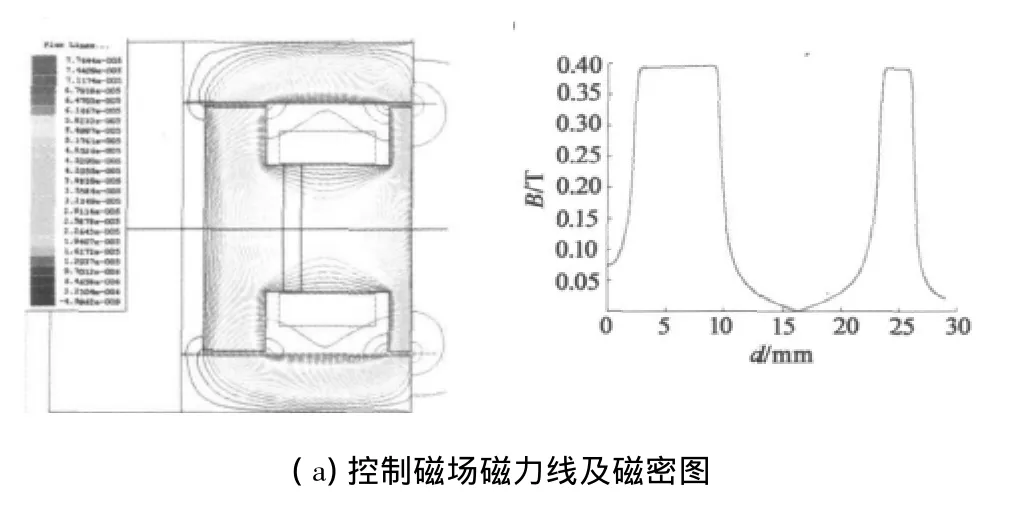
图3 磁轴承有限元仿真分析图

根据设计结果，再利用磁路法和有限元分析两种方法对磁轴承性能曲线进行计算，如图4所示。其中图4a为力/电流关系曲线，图4b为力/位移关系曲线，从结果可见，两个关系曲线都为线性关系，这就表明该型磁轴承控制性能良好。另从图中可以看出，由于磁路分析中在有效磁路外考虑了气隙漏磁系数，因而在偏置位移及电流较小时与有限元场分析的结果非常接近。

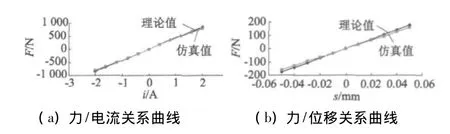
图4 永磁偏置轴向磁轴承计算结果

5 结 语

(1)永磁偏置轴向磁轴承利用位于轴向定子中的环形永磁体提供偏置磁通，结构紧凑，功耗低。采用圆盘状的转子铁心，轴向长度短，临界转速高。控制磁通和偏置磁通都只在轴向流通，与径向完全解耦，控制性能良好。

(2)利用内外气隙的控制磁通漏磁系数来分配内外磁极面积的参数设计方法，很好地解决了该型磁轴承由于结构原因所导致的内外气隙中控制磁密不等的问题，并通过调整永磁体在轴向定子中的位置，实现了内外气隙中偏置磁密相等。同时，还给出了其它结构参数的设计方法。结果表明，理论分析合理，参数设计准确。

［1］ 戴兴建，唐长亮，张剀.先进飞轮储能电源工程应用研究进展［J］.电源技术，2009(11):1026－1028.

［2］ Schweiter G，Bleuler H，Traxler A.Active Magnetic Bearings－Basics，Properties and Applications of Active Magnetic Bearings［M］.ETH，Switzerland:Hochschlverlag AG，1994.

［3］ 赵旭升，邓智泉，王晓琳，等.永磁偏置磁轴承的研究现状及其发展［J］.电工技术学报，2009，29(9):9－20.

［4］ 赵旭升.八磁极永磁偏置径向磁轴承磁悬浮机理研究［J］.微特电机，2008(6):7－9.

［5］ Pichot M A，Kajs J P，Murphy B R，et al.Active magnetic bearings for energy storage systems for combat vehicles［J］.IEEE Transactions on Magnetics，2001，37(1):318－323.

［6］ Zhilichev Y.Analysis of a Magnetic Bearing Pair with a Permanent Magnet Excitation［J］.IEEE Transactions on Magnetics，2000，36(5):3690－3692.

［7］ Kimman M，Langen H，Schmidt R M，et al.Design and realization of a miniature milling spindle with active magnetic bearings［C］//Proc 11th International Symposium on Magnetic Bearings.Japan，2008:255－260.

［8］ Oberbeck C，Ulbrich H.Active Compensation of the Elgen－Dynamics of Electromagnetic Actuators by Ecu－Based Non－linear Feedback Control［C］//Proc 7th International Symposium on Magnetic Bearings，ETH，2000:425－430.