基于微分几何反馈线性化的PMSM混合H2/H∞控制
2011-11-20严大虎纪志成
严大虎,纪志成
(江南大学,江苏无锡214122)
0 引 言
永磁同步电动机(以下简称PMSM)具备优良的低速性能,功率密度大、效率高、体积小、惯性低、响应速度快等优点,宽调速使其适应高性能伺服驱动的要求,随着永磁材料性能的不断提高和低价格,PMSM在工业生产自动化领域中的应用越来越广泛[1]。
由于现代控制理论中,对被控对象动态特性的描述中过度依赖于数学方法,并且无法高效抑制系统实际运行中所遇到的内部参数摄动和外部干扰,使之很难推广应用到工业控制中。因此发展出了以稳定性理论为基础的H∞控制方法[2],该方法具有良好的抗干扰能力,这就等同于系统具有较大的稳定裕度,但是为了获取足够大的稳定裕度,就会损失系统的其他性能。为了解决这些困难,在H∞控制理论的基础之上发展出了混合H2/H∞控制方法,该方法较好地解决了系统鲁棒性与其他性能要求之间的矛盾[3-5]。
PMSM是一个非线性、多变量、时变被控对象,由于电机参数变化和负载扰动等不确定因素的影响,使得电机高精度控制较难实现。反馈线性化控制通过非线性状态反馈和坐标变换,将PMSM的非线性数学模型实现动态解耦和全局线性化[6-7]。本文首先采用微分几何理论,将PMSM的非线性数学模型变换成线性模型,然后以该线性模型作为被控对象,考虑电机实际运行中的外部干扰以及电机未建模系统动态,设计混合H2/H∞鲁棒控制器,并采用Matlab/Simulink仿真平台对系统进行仿真验证,仿真结果表明系统的抗干扰能力较强,同时具有良好的稳、动态性能。
1 PMSM数学模型及其反馈线性化
本文的研究对象是表面式PMSM,它是一个高阶、非线性、强耦合的系统,电磁关系非常复杂,为了简化PMSM的数学模型,做如下假设[8]:
(1)忽略磁饱和,不考虑铁心的涡流损耗和磁滞损耗,磁路是线性的;
(2)电机定子电枢绕组的空载电势是正弦波;
(3)定子绕组三相对称,各相绕组的轴线在空间上互差120°电角度;
(4)忽略磁场的高次谐波,定子绕组电流在气隙中只产生正弦分布的磁势;
(5)永磁体的电导率为零;
(6)转子上没有阻尼绕组。
表面式PMSM在d-q坐标系下的数学模型:
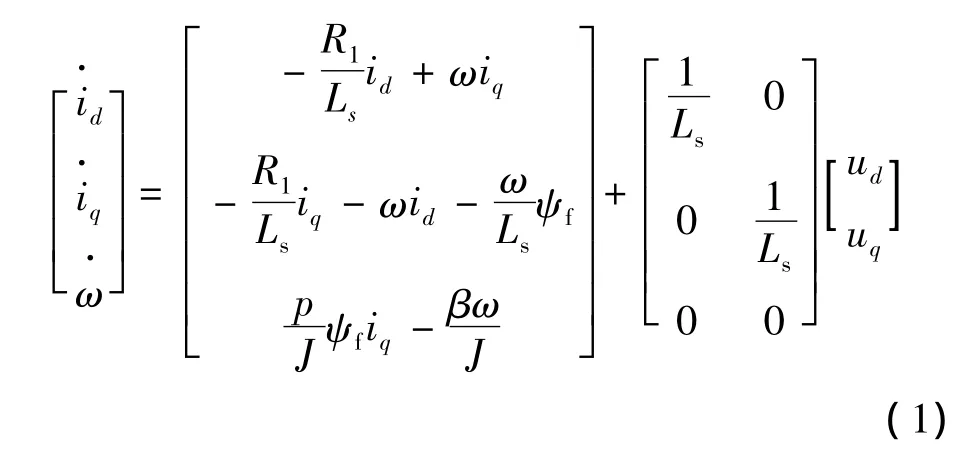
式中:id、iq分别为定子绕组d、q轴电流;ω为转子角频率;Ls为三相永磁同步电动机d、q轴的主电感;R1是定子电阻;Tl为负载转矩;p为转子的磁极对数;β为摩擦系数;J为转动惯量;ψf为转子磁场对定子的交链。
由式(1)可以看出,PMSM的模型是非线性数学模型,本文采用微分几何线性化方法对其进行精确线性化。首先将该模型转换成仿射非线性系统的标准形式,仿射非线性变换的定义如下[9]:
定义1:若变换S:Rn→Rn,S(x)=T(x)+a,T是非奇异线性变换,α∈Rn,则S称为仿射变换。
由上可得,PMSM的数学模型可以变换成如下形式:
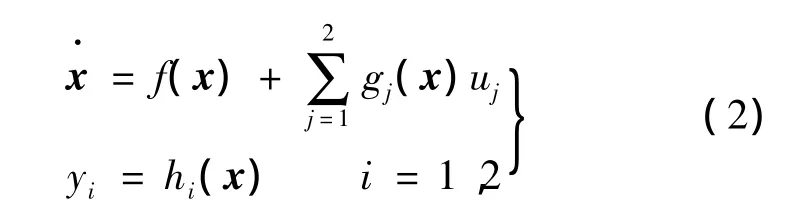
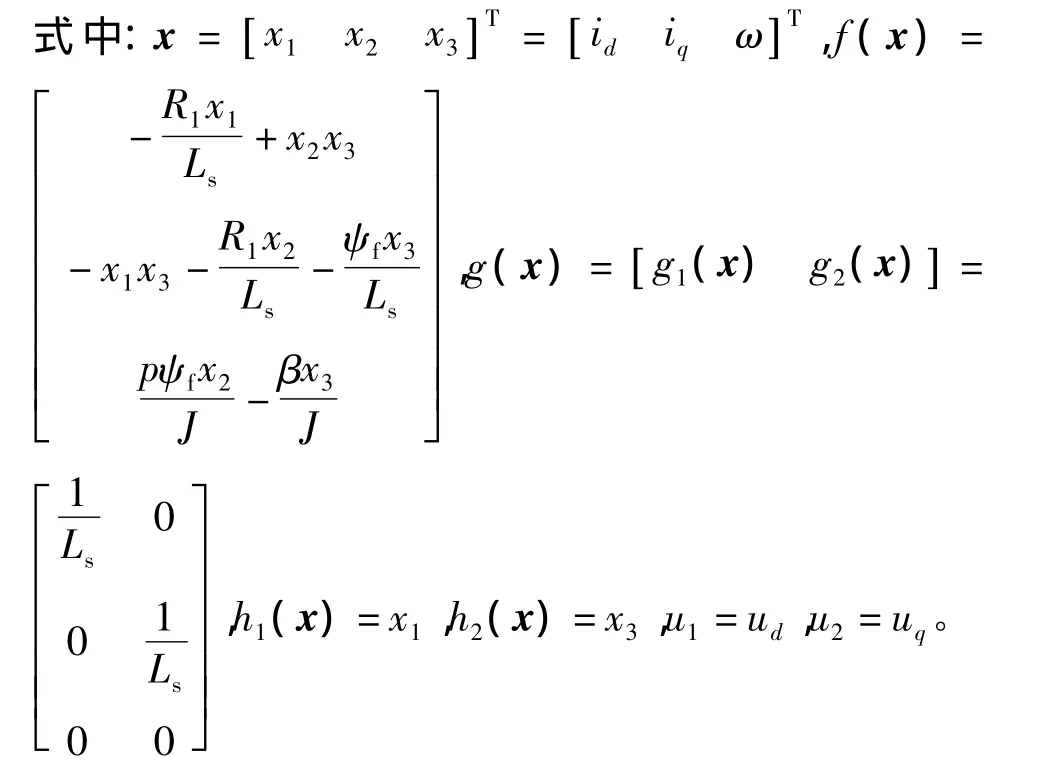
1.1精确反馈线性化条件
针对多输入多输出仿射非线性系统,系统可精确线性化的条件如下[10]:
引理1:给定的仿射非线性系统式(2),系统在x0点精确线性化问题可解的充要条件是满足:
(1)Di=Span,…,m;s≤i-1},i=1,2,…,ni为在x0点非奇异的对合分布;
(2)DimDn(x0)=n。
仿射非线性系统向量相对阶的定义如下:
定义1:给定x0∈X,如果存在x0的一个邻域V及整数向量(r1,…,rm)满足条件:
(1)LgjLkfhi(x)=0,∀x∈V,0≤j≤m,1≤i≤m
及0≤k≤ri-2;
(2)矩阵:
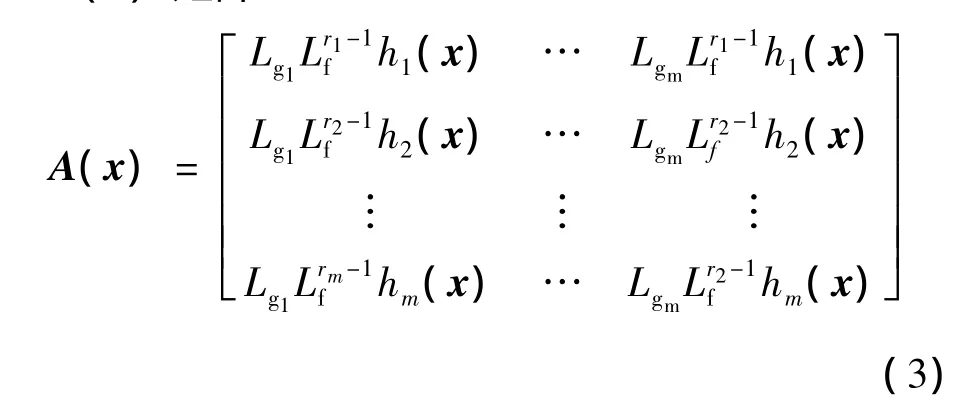
是非奇异的,∀x∈V,则称多输入多输出仿射非线性系统具有向量相对阶(r1,…,rm)。
由定义1,针对仿射非线性系统式(2)有:

所以电流环的相对阶r1=1;又有:
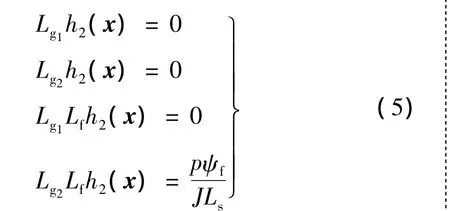
所以速度环的相对阶为r2=2。又因为矩阵:

非奇异,可得系统总的相对阶:r=r1+r2+r3,与系统维数相等,因此该系统可以实现精确线性化。
1.2坐标变换及控制率求取
引入非线性坐标变换z=Φ(x),其中:

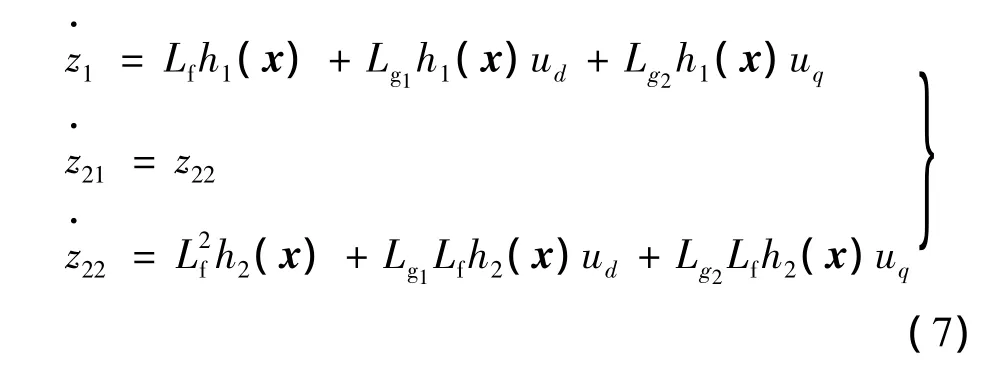
在新的坐标系下系统的状态方程如下:取控制作用u=A-1(x)[-b(x)+v],其中u为电机控制量,u=[u1u2]T,v为虚拟控制量,v=
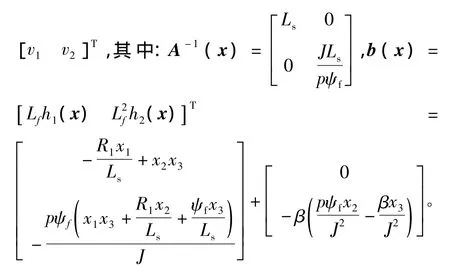
在控制作用u下,系统可以解耦为如下相互独立的线性子系统:

PMSM反馈线性化系统框图如图1所示。

图1 基于微分几何反馈线性化PMSM系统框图
2 H2/H∞控制器的设计
2.1 问题描述
考虑具有多个性能指标要求的系统:

式中:x∈Rn是状态向量,u∈Rm是控制输入,w1、w2∈Rq是两类不同的外部扰动输入,当H2范数是在随机意义下考虑时,w2是独立零均值的白噪声,w1是区别于w2的一般意义下的扰动输入,该扰动是确定的,但是具有有限能量的。z∞,z2∈Rr分别为衡量系统闭环传递函数的H∞范数和H2范数的受控输出,A,B,B1,B2,C1,C2,D10,D11,D20,D22是描述系统的已知适维矩阵(注:本节中所使用的符号均只在本节有效)。
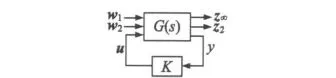
图2 混合H2/H∞标准控制结构框图
混合H2/H∞控制问题就是设计一个状态反馈控制率:

使得对于有限能量的干扰w1、w2,闭环系统满足如下性能指标[4-5]:
(1)闭环系统渐进稳定,即系统状态矩阵的所有特征值都在左半开平面中;
(2)从w1到z∞的闭环传递函数矩阵Tz∞w1满足:‖Tz∞w1‖∞<γ∞;
(3)从w2到z2的闭环传递函数矩阵Tz2w2满足:‖Tz2w2‖2<γ2。
其中,γ∞为预先给定的闭环系统扰动抑制程度,γ∞越小,表示系统抑制干扰能力越强,同时系统的稳定裕度越大,γ2应该尽可能小,以保证系统具有良好的稳、动态性能。则采用如式(10)所示的状态反馈控制率的闭环系统可表示如下:
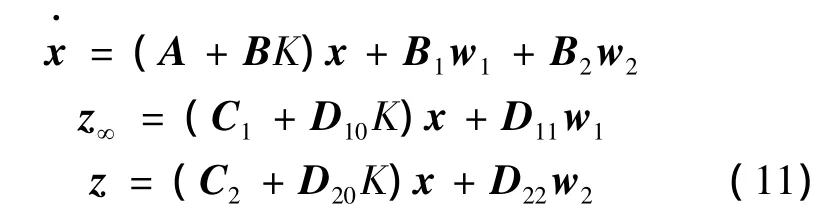
2.2 混合H2/H∞控制器求解
PMSM复杂的运行工况使其不可避免地受到外部环境的干扰,主要体现在电机负载转矩的脉动,同时,绕组电阻也会随着电机温度的变化而变化,成为电机模型的一种不确定因素。
在实际应用中,不可能实现将模型的不确定性和外部干扰与系统的输出完全解耦,因此设计如下H∞鲁棒性能指标,使干扰对系统的输出影响最小:
(1)闭环系统稳定;
(2)∀ε>0,正定矩阵Q>0,R>0和∀T>0,满足:故取性能指标函数:
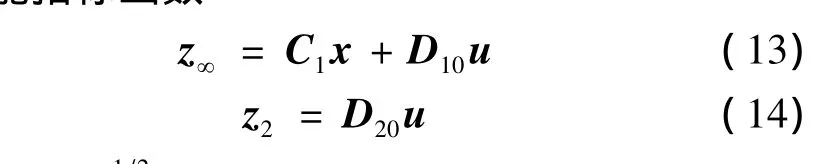
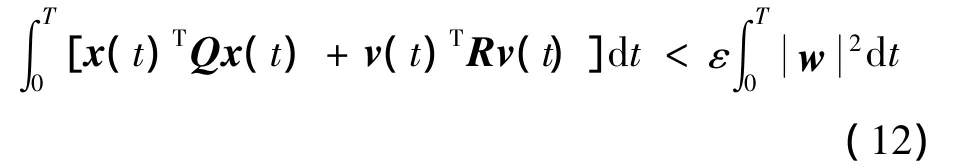
引理2[3]针对闭环系统式(11)和一个给定的标量γ∞>0,若D22=0,且以下优化问题:

有一个最优解X、W,则式(11)的状态反馈控制问题是可解的,且u=WX-1x是式(11)的一个状态反馈H2/H∞控制率。
3 仿真分析
电机参数如表1所示。
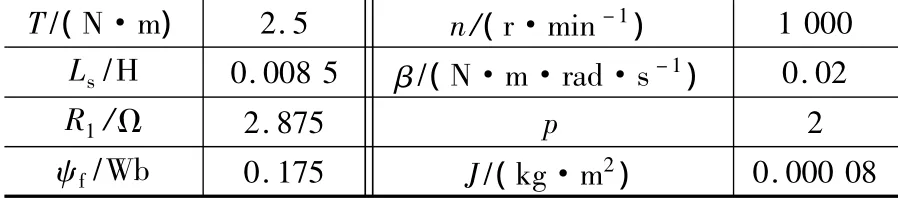
表1 PMSM参数
权系数:
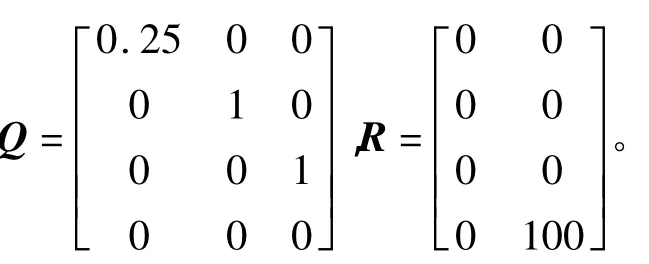
运用LMI工具箱,可求得:

其中:δ(t)=0.2+sin(0.1π)t+2sin(0.2πt)+1.25sin(πt)+0.4sin(5πt)。
在Matlab 7.0/Simulink中搭建系统仿真框图,仿真设计如下:
(1)电机带负载起动,附加干扰作用d(t),d轴电流给定i*d=0,负载转矩Tl=1 N·m,t=25 s时,电机速度给定由ω*=100 rad/s突变到ω*=180 rad/s。
(2)电机带负载起动,附加干扰作用d(t),负载转矩Tl=0.5 N·m,速度给定ω*=100 rad/s,d轴电流给定i*d=0,t=25 s时,负载转矩由Tl=0.5 N·m突变至Tl=1 N·m。
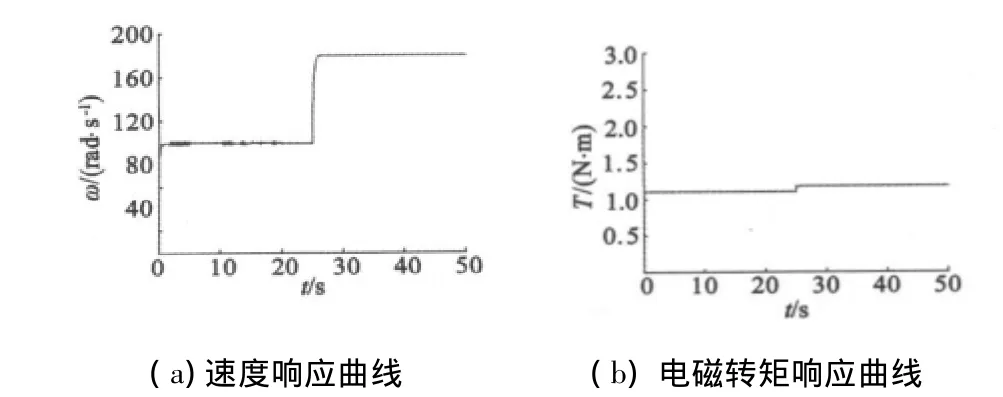
图3 速度给定跃变

图4 负载跃变
从图3的仿真结果可以看出,基于混合H2/H∞控制器的永磁同步伺服系统具有很好的稳、动态性能,可以很好地跟踪速度给定信号,电机带负载Tl=1 N·m不变,速度给定出现跃变时,电机的速度能够很快跟踪给定,且稳定后没有静差。当系统存在外部干扰时,没有对电机速度构成明显的影响,说明该系统在能够保持稳定的同时,可以达到良好的控制效果,符合H2/H∞控制器的控制特点。
从图4的仿真结果可以看出,当电机速度给定保持ω*=180 rad/s不变,负载跃变时,有较小的速度降落,并逐渐跟踪到给定速度,稳定后没有速度静差,转矩响应快速而稳定,转矩超调小,对机械机构的冲击较小,提高了其工程应用的合理性。
4 结 语
本文首先对PMSM非线性模型进行精确反馈线性化,通过非线性状态变换和反馈控制率的求取,将PMSM的非线性数学模型转化成线性模型,方便了伺服系统的设计。同时考虑了电机在实际运行过程中可能出现的外部扰动,设计了混合H2/H∞控制器,能够很好地抑制系统的外部干扰,在保持系统稳定的同时达到了良好的控制效果。仿真结果表明该系统设计方案具有很强的抗干扰能力,速度响应快,控制精度高,并且易于工程实现。
[1] Hao S,Zheng W,Hao M,et al.Simulation and development environment for digital controlled PMSM servo system[C]//Proceedings the First International Conference,ICIRA 2008,5315(2):566-575.
[2] 梅生伟,申铁龙,刘志康.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2003.
[3] 吴定会,李元龙,纪志成.基于H2/H∞状态反馈风能转换系统双频环优化控制[J].太阳能学报,2010,31(9):1185-1190.
[4] 王进华.混合H2/H∞鲁棒控制器设计[J].控制理论与应用,2004,21(1):45-53.
[5] 孙宜标,金石,王成元.基于线性矩阵不等式的环形永磁力矩电机的H2/H∞静态输出反馈控制[J].中国电机工程学报,2007,27(15):8-14.
[6] Khorrami F,Krishnamurthy P,Melkote H.Modeling and adaptive nonlinear control of electric motors[M].New York:Springer,2003.
[7] Wu F,Zhang X,Ju P,et al.Decentralized Nonlinear Control of Wind Turbine with Doubly Fed Induction Generator[J].IEEE transactions on power systems,2008,23(2):613-621.
[8] Moussa M E,Gaber Y,El Atter M,Vector Control Drive of Permanent magnet Motor without a Shaft Encoder[C]//Proc.IEEE Conf.2008:249-254.
[9] 曾文锋,李树山,王江安.基于仿射变换模型的图像配准中的平移、旋转和缩放[J].红外与激光工程,2001,30(1):18-19.
[10] 曹建福,韩崇昭,方洋旺.非线性系统理论及应用(第二版)[M].西安:西安交通大学出版社,2006.
[11] 俞力.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.
