“七桥问题”及其对数学教育的启示

胡重光

（湖南第一师范学院，湖南长沙 410205）

“七桥问题”及其对数学教育的启示

胡重光

（湖南第一师范学院，湖南长沙 410205）

通过对欧拉《哥尼斯堡桥》一文的分析，揭示了欧拉解决“哥尼斯堡七桥问题”的过程中体现的重要数学思想、策略和方法，尤其是数学化思想。这些思想、方法和策略正是我国目前数学教育的薄弱环节，对数学创新型人才的培养和数学问题解决的教学具有重要的启示。

哥尼斯堡七桥问题；数学教育；数学化

数学家是怎样解决数学问题的，对数学教育无疑具有极高的价值。但是数学家很少介绍他们的研究工作。A.A.斯托利亚尔认为，介绍怎样研究数学比研究工作本身更困难[1]。确实，庞加莱说过：数学创造是从大量的组合中作出选择，而“指导这种选择的规则是极为微妙的。几乎不可能准确地陈述它；它们只可意会而不可言传。”数学发现往往并非一个渐进的过程，而是在艰苦的工作之后瞬间产生的顿悟[2]23。庞加莱发表这些见解的那篇题为“数学的创造”的文章，曾被许多研究者提到。

然而，欧拉曾撰写一篇文章，详细地介绍了他解决“哥尼斯堡七桥问题”的过程。这篇文章题为“哥尼斯堡桥”，与《数学的创造》一起被收入M·克莱因主编的《现代世界中的数学》一书。“哥尼斯堡七桥问题”被认为开创了拓扑学的研究，在数学史上小有名气，但这篇文章却很少有人提到。“哥尼斯堡七桥问题”有两个特点：第一，它完全来自于现实，没有经过任何数学加工；第二，它属于一个全新的数学领域，以前还没有人研究过。欧拉的解答虽然并非像广泛流行的说法那样采用了“网络”，但仍具有很强的创新性，对数学教育有重要的启发。本文拟作一个初步的分析。

一、欧拉的解答

“哥尼斯堡七桥问题”是我们熟知的：如图1，在哥德的诞生地普鲁士哥尼斯堡城有一座奈霍夫岛（岛A），普雷格尔河的两条支流绕它流过。那里有7座桥（a、b、c、d、e、f、g）跨过两条支流。问：一个人能否计划一次散步，使得每一座桥都通过一次而且仅仅一次？

图1

一般人碰到这种问题，首先会试图找出各种可能的路线，逐一检验。而欧拉则认为，这样做一方面是太繁锁，另一方面这种解决法只适合这一个问题，没有普遍意义。因此，欧拉一开始就着眼于找出这类问题的一般解法。

欧拉解决这一问题的第一步是，找出一种描述路线的简单方法。他用A、B、C、D分别表示被河流分割的陆地区域，由地点A跨越桥a或b走到地点B则记为AB，如再由B跨越桥f走到地点D则记为ABD。中间的字母B既表示第一次跨越的终点，又表示第二次跨越的起点。其余依此类推。由此他发现：

1.这种表示法与跨越的桥无关，例如从A跨越桥a或b到B，都记为AB；

2.跨越n座桥的路线恰好由n+1个字母表示。

于是问题就转化为用A、B、C、D四个字母组成一个合条件的8个字母的排列。由于有的区域不只一座桥相连，有的字母会重复出现，因此必须确定每一个字母出现的次数。

为了找到判断某个字母出现次数的法则，欧拉取一个单独的区域A，并设有任意多座桥a、b、c、d、……通向A（如图2）。这样散步者可以通过不同的桥多次进入或离开A，而字母A出现的次数就由通过的桥数来决定。

图2

欧拉发现当桥数为奇数时，两者之间的规律如下表：

桥数 A出现的次数113253……2n-1N=[(2n-1)+1]/2

也就是说，字母A出现的次数等于桥数加1的和再除以2。

当桥数是偶数时，则须考虑A是出发地点还是到达地点。如果A是出发地点，则字母A出现的次数是桥数的一半加1；否则是桥数的一半。

每条线路都有一个出发点，其余为到达点。根据上述分析，计算线路中字母出现的次数和所有字母出现的总次数的方法是：当桥数为奇数时，将桥数加1再除以2；当桥数为偶数时，直接将桥数除以2，就得出每个字母出现的次数。当出发地点的桥数为奇数时，将这些次数相加就得所有字母出现的总次数；当出发地点的桥数为偶数时，还要将求出的和再加1。如果算出的结果等于桥数加1，则所要求的散步可以做到；否则就不能做到。

欧拉将以上的计算过程列成一个表，对于哥尼斯堡七桥问题，他列出的表如下：

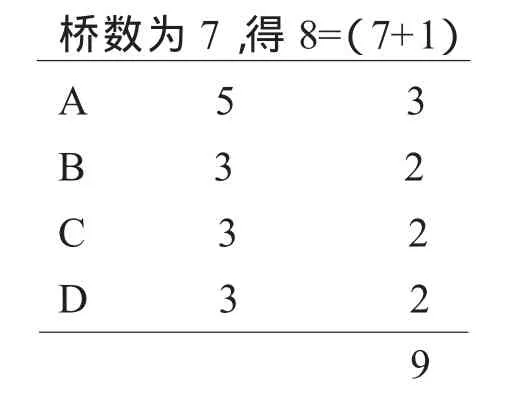
桥数为7，得8=（7+1）A53B32C32D329

最后一列数是每个字母在路线中出现的次数。由于它们的和不等于桥数加1，所以所要求的散步不能实现。

图3

欧拉还用这种方法讨论了一个例子。如图3，有两个岛被4条河环绕，有15座桥连接两岛和陆地。按以上方法欧拉列出了以下的表，并在有偶数座桥连接的字母上打一个★号：

A* 84B* 42C* 42D32E53F* 6316

计算出的字母数与所要求的相等，因此所要求的散步可以实现。但是这是按有偶数座桥的地区为到达点计算的，因此这种散步只能从两个没有标★号的地点出发。若从任一有偶数座桥的地点出发，则字母数还需加1，就超过了规定的字母数，因而满足条件的散步不能做到。

至此问题似乎已经完全解决，但是欧拉并没有到此为止。通过观察这张表，他发现了一个更简单的方法。

首先他注意到第二列数之和是桥数的2倍，原因是每座桥都被计算了两次。由此可知第二列数字之和应为偶数。这时如果每两个地点都由偶数座桥相连，那么如前所述，计算出的字母数恰好等于桥数加1（这时出发点由偶数座桥连通），在这种情况下，不管从哪一地点出发，所要求的散步都可实现。

如果有的地点由奇数座桥相连，那么这样的地点一定是偶数个。如果恰有2个这样的地点，那么按前面的计算方法，得到的字母数恰好等于桥数加1，所要求的散步能够实现；如果有4个或更多的这样的地点，则求得的字母数将大于桥数加1，所要求的散步不能实现。

总之，对于任何这类图形，确定不重复地走遍所有的桥是否可能的最简单的方法是：

如果有多于两个地点由奇数座桥相连，则不存在满足条件的路线；

如果只有两个地点由奇数座桥相连，只要从这两个地点之一出发，所要求的散步就可以实现，但终点只能是这两个地点中的另一个；

如果所有地点都由偶数座桥相连，则不论从哪一地点出发，所要求的散步都可以实现，并且可以回到起点。

这三条法则彻底解决这类问题。

二、欧拉解法中的重要数学思想方法

分析欧拉的解答过程，可以发现以下的重要数学思想、策略和方法：

（一）一般化思想

欧拉在解答中，始终着眼于找出一般的解法。他一开始就指出了这一点，在解答的过程中也始终坚持这一点。这样就使这一个别问题的解法具有普遍意义，并且简化了这一问题的解答。如果欧拉不坚持这一点，哥尼斯堡七桥问题就不会成为拓扑学（欧拉当时称之为“位置几何”）的开端。这一点正体现了数学家超越常人的眼光。

（二）数学化思想

解答这一问题最重要的策略是先将问题数学化，具体来说，就是用数学语言来表达散步的线路。正如欧拉指出的：“我的整个方法基于以下我用来表示越过桥梁的合适的和方便的方法。”[2]236正是这种表达方式使问题简化，容易发现其中的规律。发现这种表达方法也就是建立了一个简单的数学模型，由此可见，建立数学模型在数学问题解决中是最基本的、至关重要的。

（三）简化策略

解决这一问题的另一个重要策略是将问题简化，考虑它的尽可能简单的情形。在本题中，欧拉首先考虑只有1条河流这种最简单的情形，从而较容易地发现了线路表达中字母出现次数的规律。

尽可能地简化问题是解决数学问题的一个重要策略，我国著名数学家华罗庚说：善于“退”，足够地“退”，“退”到最原始而不失去重要性的地方，是学好数学的一个诀窍！

（四）列表方法

还有一个值得注意的方法是将数据列成表，欧拉在解答过程中三次运用了这一方法。这一看来很简单的方法却是应用广泛和十分有效的，而且很容易掌握。数学家在他们的研究工作中是经常利用列表来整理信息和组织思维的，并视其为一种基本方法。笛卡尔就曾指出：“所谓方法，就是把我们应当注意的事物进行整理和排列。”[3]列表的优越性一是能使思维有条理，二是便于发现其中的规律。第二条尤其重要，欧拉正是通过观察所列的数表发现了简便方法。

三、欧拉解法的数学教育意义

这四条对于数学教育特别是数学问题解决都具有重要的意义，也是我国数学教育的薄弱环节。我国的数学教育偏重解题的特殊方法和技巧，花大量的时间解答各种类型的题目；重视公式、定理的运用，而忽视通过数学化建立数学模型这一解决问题的一般方法和有力工具。结果就导致学生记题型，套解法；习惯于用现成的公式、定理解题，不善于探索那些非常规的和没有进行数学加工的问题的解法，对于“七桥问题”这类没有任何公式可套、几乎没有数学知识可用的现实问题，往往束手无策。“数学化”是弗赖登塔尔数学教育思想的一个重要概念，他有一句名言：与其说是学习数学，不如说是学习“数学化”。而这一重要思想在我国的数学教育中还没有得到应有的重视。改变这种状况，应该是我国目前数学教育改革的最重要和迫切的任务。

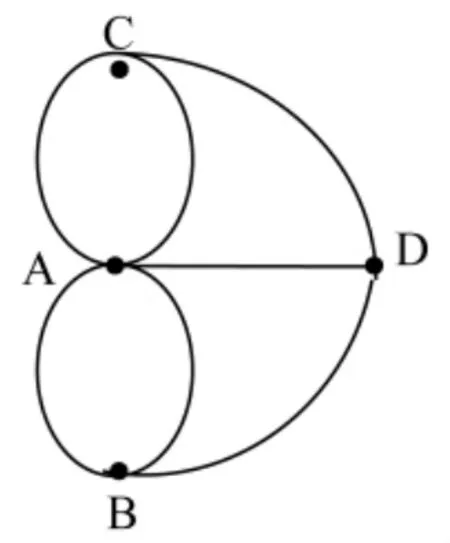
图4

最后指出一点，解决问题的数学模型往往不止一种。对于“七桥问题”，进一步的研究发现，以上解法中的数学模型还可以进一步简化。因为这个问题与岛和陆地的面积、桥和路的长短、方向等几何量都无关，所以可以用点来表示岛和陆地，用线来表示桥，这样就可以将图1最大限度地简化，转化为图4。其中A是岛屿，B、C、D是陆地，AB、BA、AC、CA、AD、CD、BD七条线分别代表7座桥。而问题也就转化成：能否从图4的A、B、C、D中的任意一点出发，不重复也不遗漏地一笔画完图4中的所有两点间的连线？根据图中顶点的奇偶性，很容易得出欧拉所发现的那3条法则。这就是我们熟悉的“一笔画”问题，而这个图属于拓扑学中的“网络”。

[1]A.A.斯托利亚尔.数学教育学[M].北京:人民教育出版社,1984:107.

[2]Morris Kline.现代世界中的数学[M].上海:上海教育出版社,2004.

[3]G.波利亚.数学的发现：第二卷[M].北京:科学出版社,1987:437.

“Seven BridgesProblem”and itsInspiration on Mathematics

HU Chong-guang

(Hunan First Normal University,Changsha,Hunan 410205)

This paper has revealed Euler’s mathematical thinking and strategy in the process of resolving“seven bridges problem”on the basis of his remarkable articleThe Bridge of Koenigsberg.Euler’s thinking and strategy are the weaknesses of modern mathematics,which will give some enlightenments for teaching and training of creative mathematical studentsstudents.

Seven BridgesProblem;mathematical education;mathematicization

G633.6

A

1674-831X（2011）06-0014-03

2011-09-01

湖南省教育科学“十一五”规划重点课题（XJK08AJJ005）；湖南第一师范学院院级课题（XYS09Z01）

胡重光（1950—），男，湖南道县人，湖南第一师范学院教授，主要从事数学教育研究。

[责任编辑：胡 伟]