问题教学的“过程化”研究

陈秀琼

（湖南第一师范学院，湖南 长沙410002）

问题教学的“过程化”研究

陈秀琼

（湖南第一师范学院，湖南 长沙410002）

问题教学是指以问题为中心的教学，它是把教学内容化作问题，引导学生通过解决问题从而掌握知识、形成能力、养成心理品质的过程。以数学教学中数学概念的形成过程、数学定理、公式和法则的发现及推导过程、数学问题解决的认知过程为例，探究问题教学的“过程化”。

探究；问题教学；过程化

问题教学的早期发展，可以追溯到古希腊苏格拉底的精神助产术。在我国古代，也早就有了“学起于思，思源于疑”的说法。关于问题教学，有多种不同的看法。一般认为，所谓问题教学，是指以问题为中心的教学，它是将教学内容化作问题，引导学生通过解决问题从而掌握知识、形成能力、养成心理品质的过程。它至少具有以下三个特点：其一，是教师教学方式的启发性和指导性，学生学习方式的独立性和发现性。其二，是学生学习过程的积极主动性。其三，是学习结果的创造性。在数学课堂开展问题教学，旨在真正实现师生互动，培养学生分析问题和解决问题的能力，凸显数学教学的“过程化”——即更加强化“在数学教学过程中展示知识的形成过程，而不仅仅是结果”这样一种教学理念。

一、揭示数学概念的形成过程

数学概念是反映数学对象本质属性的思维形式，是数学思维的载体，是构成数学学科知识的基本成分。因此，理解概念是一切数学活动的基础，概念教学是数学课堂教学的重要内容。运用问题教学学习数学概念会让学生经历如下过程：感知—理解—深化。

例如，一元二次方程的教学。

在课前预习中，向学生发放同样大小的长方形硬纸板，并要求学生“利用这块硬纸板做成一个没有盖的长方体盒子”，让学生利用课余时间自行设计，自我制作，自己体会，并总结出制作无盖纸盒的方法。

1.创设问题情境，感知概念

教师拿出自己制作的无盖长方体纸盒的模型，并指出：制作这个模型的纸板的长为80cm,宽为60cm,做成的无盖纸盒的底面面积为1500cm2，要求同学们拿出自己制作的无盖长方体纸盒模型，量一量该模型的底面的长和宽，并计算出自己做成的无盖纸盒的底面面积。你能提出什么问题？

2.分析和讨论，归纳概念

教师根据同学们提出的问题，结合自己设计的问题，整理如下：

（1）你的无盖长方体模型是怎样做出来的？

（2）为什么同样大小的长方形纸板，做出来的无盖长方体的盒子的底面面积不同？

（3）无盖长方体纸盒的底面面积与截去的小正方形边长有关吗？

同学们以小组为单位进行分析讨论，合作交流。在教师的引导点拨下，得到如下结论：

（1）无盖长方体纸盒的底面面积与截去的小正方形边长有关；

（2）由于截去的小正方形边长不同，所以无盖长方体纸盒的底面面积不同；

接下来，教师因势利导，让学生归纳出一元二次方程的概念，再由教师补充完善。

3.反思，深化概念

形成概念后，教师要求学生思考：

（2）如果你用来制作模型的长方形纸板的长和宽分别为acm和bcm,(a和b均为已知量)，设截去的小正方形边长为cm，为未知量，能得出什么结论？

（3）满足什么条件的方程叫一元二次方程？在这个教学设计中，教师重视了概念的具体化到抽象化的有机结合，让学生经历从“个别到一般、从感性认识到理性认识的过程。”也经历了对概念的“感知—理解—深化”的过程。

二、展现数学定理、公式和法则的发现和推导过程

由于数学定理、公式和法则是由概念组合而成，反映了数学概念之间的关系及其规律，因此，就其学习的复杂程度而言，应高于数学概念的学习。这就要求教师在重视学生正确理解和熟练应用定理、公式和法则的同时，还应强调展现定理、公式和法则的发现和推导过程。如果运用问题教学学习数学定理、公式和法则，会让学生经历“感知—探究—猜想—归纳”的过程。

例如，等比数列求和公式的教学设计

1.创设问题情景，感知数学材料

在简单复习等比数列的概念和通项公式之后，教师给出如下案例：

甲和乙准备玩一个游戏。甲对乙说：“从今天开始的30天中，我每天给你一万元，但你必须做到：今天给我1分钱，明天给我2分钱，以后每天所给我的钱数都是上一天的2倍，30天完成。”乙听后大喜，心想：他一万一万地给，我却几分几分地给，我肯定占便宜。同学们，果真如此吗？

2.分析和讨论，共同探究

教师将同学们分小组为单位，提出如下问题讨论：

（1）你们能将案例中的数学材料抽象成数学知识吗？

（2）要判断出谁占便宜，就是要比较什么？

（3）这30天中甲和乙各付出了多少钱？

（4）乙付出的钱怎么算？

通过教师引导，同学们进行了探究：

要判断出谁占便宜，就要看谁付出的钱少，也就是要分别算出甲、乙各付出了多少钱：

甲付出：30万元，乙付出：（1+22+22+23+…+229）分。归根结底，是要计算1+22+22+23+…+229，这就将案例中的数学材料抽象为数学知识。

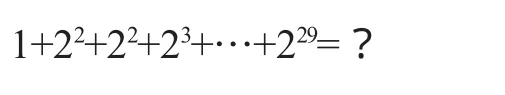
方法一：

设S30=1+22+22+23+…+229，则

S30=1+2（1+22+22+23+…+228）=1+2S29用S30替换S29，最终求得：S30=230-1，乙总共付出约1000万元。

3.类比、猜想

教师对各组表现（包括问题分析、合作交流、自主探究等）进行点评，并指出：同学们解决了一个特殊等比数列前30项的求和问题。进一步提出：如果将案例中的“2倍”改成“3倍”，能求出乙付出的钱数吗？也就是如何计算：S30=1+3+32+…+329，并猜一猜：如果改成“q倍”，结果又是怎样呢？

4.推广、归纳

师生共同对案例进行反思，然后将案例中的问题推广为：如果一等比数列的首项为，公比为q,求这个等比数列的前n项和。最后归纳出等比数列的前n项公式：

三、暴露数学问题解决的认知过程

几乎所有的教学活动都与问题有关，数学教学过程实质上是学生在数学问题解决过程中不断提升问题解决能力的过程。为了培养学生数学问题解决能力，运用问题教学是一个很好的选择，可以让学生经历“感知问题——提出问题——解决问题——延伸问题”的数学问题解决认知过程。

例如，塑料袋的统计教学

一周前给学生布置家庭作业，让每个学生统计自己家里一周丢弃的塑料袋个数。

1.创设问题情景，感知问题

教师首先要求每个学生统计数据进行汇报，并填在下面这张表格里：

然后提出问题：根据这组数据，运用所学知识，你们能说点什么？

2.分析和讨论，提出问题

通过同学们对案例的分析和讨论，在教师的引导和点拨下，提出下列问题：

（1）我们班同学的家庭一周内共丢弃多少个塑料袋？

（2）一周内平均每个家庭丢弃多少个塑料袋？

（3）这组数据的众数和中位数各是多少？它们的含义是什么？

（4）照这样下去，一年我们大概丢弃多少个塑料袋？

（5）如果把塑料袋看作长方形，大概有30cm长，20cm宽，那么，一年我们大概会污染多少土地？

3.合作交流，解决问题

要求同学们共同合作，寻求解决问题的不同方法，并相互交流，教师是引导者、组织者和合作者。

4.评价反思，延伸问题

教师对前面的过程进行评价、反思，然后引导同学们进一步提问：

（1）如果每个家庭成员以三个人计算，平均每人每天丢弃多少个塑料袋？

（2）如果我国人口以13亿计算，那么一天我们共丢弃多少个塑料袋？

（3）如果我国土地面积以960万平方千米计算，经过多长时间我国土地可能都会受到污染？

问题教学是新课程改革提倡的教学方法之一，问题教学的“过程化”强调了知识的形成过程，从而真正体现了数学思维教学的特点，实践证明这种教学方法符合学生的认知规律，也得到了广大师生的认可。通过问题教学的“过程化”，在教学实践中学生能够较好地找到知识的生长点，体验数学知识发生、发展过程，从而更好地经历由感性认识上升到理性认识的过程。正如前苏联教育家斯托利亚尔所说：“数学教学是数学（思维）活动的教学。”这应是数学教育不变的主题。

[1]郑金洲.问题教学[M].福州:福建教育出版社,2005.

[2]于忠海.案例教学应用于新课程的价值与实施策略[J].天津师范大学学报:基础教育版,2004.(4)

[3]冯斌.简论数学教学的“过程化”[J].数学通报,2004,(10) [4]龙应时.数学概念的教学要让学生经历过程[J].中学数学:初中版,2008,8.

[5]赵水祥.关于数学定理教学的思考[J].中学数学杂志:初中.2004,(6).

[6]范文贵.小学数学反思性教学研究[J].湖南第一师范学院学报，2010，（2）.

Exploration on Processization ofQuestion-Teaching

CHEN Xiuqiong

(Hunan First Normal University,Changsha,Hunan 410002)

Question-teaching is a question-oriented method,which is characterized by transformation of teaching tasks into specific questions.The question-teaching is aimed at guiding students through solving the specific problems so as to master the knowledge,gain the ability and develop their psychological quality.In this paper,the process of question-teaching was investigated through a detailed analysis of the formation process of mathematics concepts,the discovery and derivation process of mathematical theorems,formula and rules,and cognitive process of solution of mathematical problems,so asto explore the processization of question-teaching.

exploration,question-teaching,processization

G623.5

A

1674-831X（2011）05-0033-03

2011-04-14

湖南省教育厅高等学校教学改革课题（2010[450]）

陈秀琼（1967—），女，湖南茶陵人，湖南第一师范学院副教授，主要从事数学教育研究。

[责任编辑：胡 伟]