一类二阶微分方程的特征值估计及其反问题

王於平， 杨传富

（1.南京林业大学理学院应用数学系，江苏南京 210037； 2.南京理工大学理学院应用数学系，江苏南京 210094）

一类二阶微分方程的特征值估计及其反问题

王於平1， 杨传富2

（1.南京林业大学理学院应用数学系，江苏南京 210037； 2.南京理工大学理学院应用数学系，江苏南京 210094）

借助Rouché定理及渐近分析的方法，给出了边界条件含有特征参数的一类二阶微分方程的特征值渐近公式.运用特征值渐近公式给出了特征值反问题的一个惟一性结果及重构公式.

二阶微分方程；参数边值条件；特征值渐近式；特征值反问题

本文考虑了下列边界条件含有特征参数的二阶微分方程的特征值问题

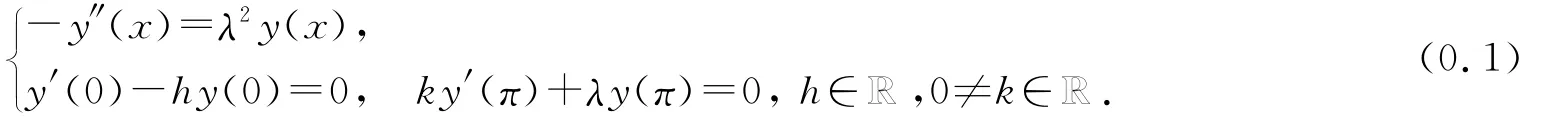
1 特征值估计

定理1问题（0.1）的特征值至多可数，记为，n∈Z Z，当｜n｜充分大时，λn是简单零点，且有估计式

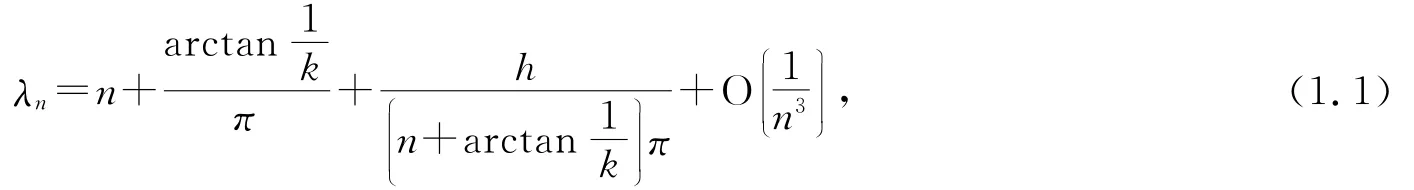
特征值对应的特征函数y n（x）＝λncos（λn x）＋hsin（λn x）.

证方程－y″（x）＝λ2y（x）的通解为

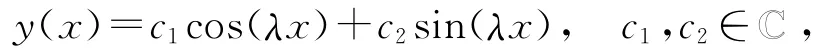
且y′（x）＝－c1λsin（λx）＋c2λcos（λx）.y（x）是问题（0.1）的特征函数必须y（x）满足问题（0.1）的边界条件，因此

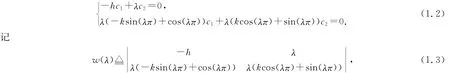
则y（x）是问题（0.1）的特征函数必须

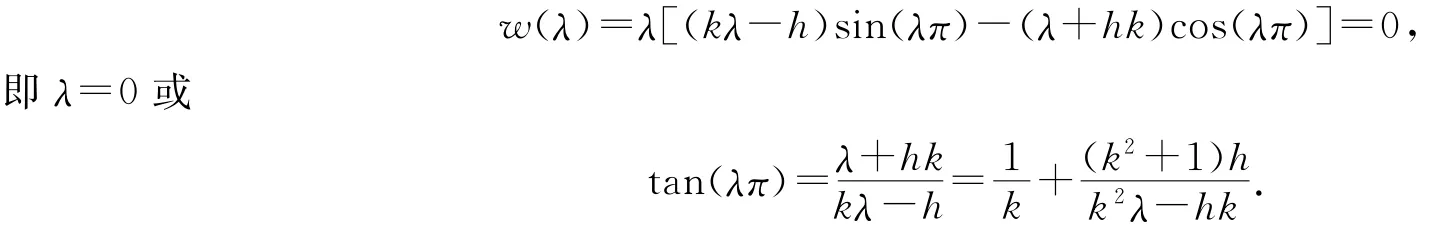
2 特征值反问题

考虑下列两个特征值问题

3 边条件参数h，k的重构

由定理2可知：对于问题（0.1），它的一组特征值可惟一确定边条件参数h，k.如果给定问题（0.1）的一组特征值，怎么由特征值构造边条件参数h，k？

［1］Fulton C T.Two－point boundary value problems with eigenvalue parameter contained in the boundary conditions［J］.Proc.Roy.Soc.Edinburgh，1997，77（A）：293－308.

［2］Hochstadt H.Asymptotic estimates of the Sturm－liouville spectrum［J］.Comm.Pure Appl.Math，1961，4：749－764.

［3］Yang C F and Huang Z Y.Inverse spectral problems for 2m－dimensional canonical Dirac operators［J］.Inverse Problems，2007，23：2565－2574.

［4］钟玉泉.复变函数论［M］.北京：人民教育出版社，2004.

Estimate of the Eigenvalue and Inverse Problem of a Class of Second－order Differential Equations

WANGYu－ping1，YANGChuan－fu2
（1.Department of Applied Mathematics，Nanjing Forestry University，Nanjing 210037，China；2.Department of Applied Mathematics，Nanjing University of Science and Technology，Nanjing 210094，China）

With the help of Rouché’s theorem and the methods of asymptotic analysis，we give asymptotic formula of the eigenvalue of a class of second－order differential equations with eigenparameter contained in the boundary conditions.A uniqueness result of inverse eigenvalue problem and reconstructions ofhandkare presented.

second－order differential equation；eigenparameter in the boundary conditions；asymptotics of eigenvalue；inverse eigenvalue problem

O174.5

A

1672－1454（2011）04－0118－04

2008－11－03；［修改日期］2009－05－18

南京理工大学教学改革项目（AB42640）；南京理工大学基金项目（AB41366，AE88787）；江苏省自然科学基金（BK2010489）