一个含有多个参量的Hilbert型不等式

张凤平， 谢子填

（1.广东新兴惠能中学，广东新兴 527400； 2.广东肇庆学院数学系，广东肇庆 526061）

一个含有多个参量的Hilbert型不等式

张凤平1， 谢子填2

（1.广东新兴惠能中学，广东新兴 527400； 2.广东肇庆学院数学系，广东肇庆 526061）

应用权系数方法给出的一个新的带有最佳常数和多个参量的Hilbert型不等式.同时给出他的等价形式.

Hilbert不等式；权系数；Hölder不等式

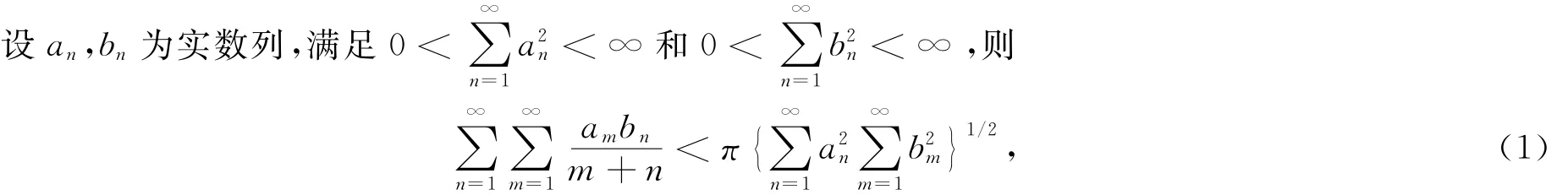
这里常数π为最佳值.上式推广为

设p＞1，1／p＋1／q＝1，且右边级数收敛于正数时，有

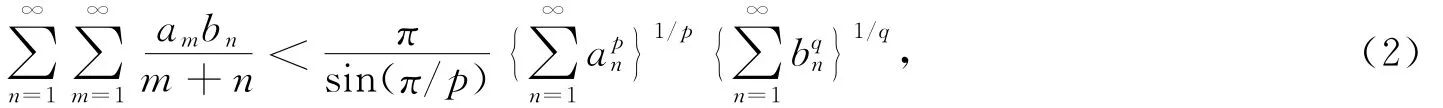
不等式（1）和（2）在分析学有重要应用.近年来，杨必成等人对这些不等式陆续作了推广［2，3，5－14］，文章［4］对［3］的结果作了改进.2004年，他证明了［2］：

设p＞1，1／p＋1／q＝1，an≥0，bn≥0，右边级数收敛于正数时，则以下有最佳常数因子的不等式：的类似带有最佳常数的不等式，并给出其等价形式.

如无特别声明，我们假定a＞0，b＞0，c＞0，e＞0，1／2≥μ＞0，ae≠bc；p＞1，1／p＋1／q＝1.

引理1定义权系数如下：

［1］Hardy G H，Littlewood J E and Polya G.Inequalities［M］.Cambridge：Cambridge University Press，1952.

［2］杨必成.一个推广的Hardy－Hilber不等式［J］.数学年刊（A辑），2002，23（1）：247－252

［3］杨必成.参量化的Hilbert不等式［J］.数学学报，2006，49（5）：1121－1126.

［4］王文杰，贺乐平，陈铁灵，参量化的Hardy－Hilbert型不等式的改进［J］.湘潭大学自然科学学报，30（2）：13－15.

［5］谢子填.一个核为－3μ齐次的Hilbert型不等式［J］.吉林大学学报（自然科学版），2007，45（3）：369－373.

［6］谢子填，曾峥.一个含有参量的Hilbert型不等式［J］.湘潭大学自然科学学报，2007，29（3）：24－28.

［7］谢子填.一个核含无理式的Hilbert型不等式［J］.数学的实践与认识，2008，38（16）：128－133.

［8］Xie Zitian.A new reverse Hilbert－type inequality with a best constant factor［J］.J.Math.Anal.Appl.2008，343：1154－1160.

［9］谢子填，付本路.一个新的有最佳常数的Hilbert型积分不等式［J］.武汉大学学报（理学版），2009，55（6）：637－640.

［10］Zeng Zheng and Xie Zitian.On a new Hilbert－type integral inequality with the integral in whole plane［J］.Journal of Inequalities and Applications，Vol.2010，Article ID 256796，8 pages，2010.doi：10.1155／2010／256796.

［11］谢子填，杨必成，曾峥.一个新的齐次核的Hilbert型积分不等式［J］.吉林大学学报（理学版），2010，48（6）：941－945.

［12］谢子填，曾峥.一个新的有最佳常数因子的Hilbert不等式［J］.湘潭大学自然科学学报，2010，32（3）：1－4.

［13］Xie Zitian，Zeng Zheng.A Hilbert－type inequality with some parameters and the integral in whole plane［J］.Advances in Pure Mathematics，2011（1）：84－89.

［14］谢子填，曾峥.一个实齐次核的Hilbert型积分不等式及其等价形式［J］.浙江大学学报（理学版），2011，38（3）：266－270.

［15］匡继昌.常用不等式［M］.3版.济南：山东科技出版社，2003.

A Hilbert－type Inequality with Some Parameters

ZHANGFeng－ping1，XIEZi－tian2
（1.Huineng Senior Middle School，Xinxing，Guangdong 527400，China；2.Department of Mathematics，Zhaoqing University，Zhaoqing，Guangdong 526061，China）

We give a new Hilbert’s inequality with a best constant with some parameters and factor，and its equivalent form.

Hilbert－type inequality；weight coefficient；Hölder inequality

O178

A

1672－1454（2011）04－0113－05

2008－10－23