机器带准备时间的同类机分批排序算法
2011-11-02李海霞朱路宁赵晟珂
李海霞, 朱路宁, 赵晟珂
(1.山东水利职业学院基础科学部,山东日照 276826; 2.曲阜师范大学运筹与管理学院,山东日照 276826)
机器带准备时间的同类机分批排序算法
李海霞1, 朱路宁2, 赵晟珂2
(1.山东水利职业学院基础科学部,山东日照 276826; 2.曲阜师范大学运筹与管理学院,山东日照 276826)
讨论了两类机器带准备时间的同类机分批排序问题.对工件无到达时间及有常数个到达时间,目标函数为极小化加权总完工时间这两类问题进行研究,给出了两个最优算法,并对算法及其计算复杂性给予了分析与证明.
分批排序;准备时间;FBLW算法;最优性
1 问题背景及描述
排序问题是组合最优化领域中的一类重要问题,它在生产管理与调度、晶体加工[1,2]、网络通信、航空工业[3,4]、钢铁铸造[5]、计算机数据处理以及物流管理等方面有着广泛的实际应用背景.产生于20世纪90年代的分批排序问题是从半导体生产过程的最后阶段提炼出来的一类重要排序问题[6].国内外许多专家学者对其进行了研究并取得了许多重要的成果[7-10].对目标函数为极小化加权总完工时间的平行机排序问题,Bruno和Coffman[11]证明P2‖是NP-难的,因而分批排序问题Pm|B||B|也应是NP-难的,Cheng等[12]对Pm|B|给出了时间复杂性为o(mn m+1)的动态规划算法.对于工件有不同到达时间的情况,Deng和Zhang[13]证明了1|rj,B≥n|∑ωjC j是NP-完备问题,并给出了当工件到达时间与工件加工时间个数为常数的动态规划算法.丁际环等[14]就工件具有两个到达时间的、目标函数为极小化加权总完工时间的排序问题证明了其NP-完备性,并给出了一个2-近似算法.在所有工件有相同的加工时间的特殊情况下,苗翠霞、张玉忠[15]给出了最优算法.
随着社会生产的不断发展,大量的新型排序问题不断涌现,机器带准备时间的情况便是其中之一.此前传统的经典排序问题总是假设机器在零时刻就可以加工工件,但实际情况往往并非如此,比如机器在开工之前要做日常的维护工作,在此期间不能加工工件,这段时间就称为机器的准备时间,并用Ri表示机器Mi的准备时间.由现有文献不难得到Qm,Ri|B|,排序问题也是NP-难的.
本文在[16]的研究基础上首次讨论了在所有工件的标准加工时间均相同的条件下的两类机器带准备时间的同类机排序问题.分别对工件无到达时间及有常数个到达时间,且目标函数均为极小化加权总完工时间这两类排序问题进行了研究.用三参数表示法可表示为

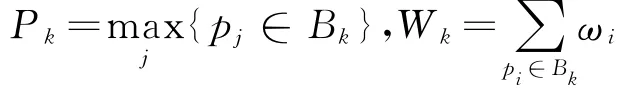
2 对于Qm,Ri∑ωjC j问题的精确算法
苗,张[17]利用复制法已给出了Pm|B|∑ωjC j的NP-完备性证明.因而易知题至少也应是NP-难的.但该问题在工件有相同的标准加工时间的情况下,却是多项式时间可解的.
FBLW算法(fully batch largest weight).
步骤1:将工件按权重不增的顺序重新编号,即ω1≥ω2≥…≥ωn.
步骤2:对工件进行分批.将前B个工件作为第一批,记为B1;次B个作为第二批,记为B2,…,依次进行下去.
步骤3:将分好的每批工件看作一个工件,按批的下标不减序依次安排在批处理机上进行加工,且不让批处理机空闲.
由FBLW算法可知,n个工件可以分为批或+1批,除最后一批不满外其余各批均是满的,显然该算法的时间复杂性为O (nlogn).
在该算法的基础上,需对其进行改进使之能够有效的解决所要研究的问题为此,结合ECTF(earliest completion time first)算法,对其作如下调整:首先,将批处理机的准备时间看作在零时刻加工的第一个工件.其次,在对每批工件进行安排时对批处理机进行选择.
改进后的算法为:
算法A1.
步骤1:将工件按权重不增的顺序重新编号,即ω1≥ω2≥…≥ωn.
步骤2:对工件进行分批.将前B个工件作为第一批,记为B1;次B个作为第二批,记为B2,…,依次进行下去.
步骤3:把批处理机的准备时间看作其在零时刻开始加工的第一个工件.
步骤4:将分好的每批工件看作一个工件,按批的下标不减序依次安排在其最早完工的批处理机上进行加工,不让批处理机空闲.
显然该算法的计算复杂性为O (nlogn).
定理1算法A1能最优的解决问题
为证明方便,算法A1中工件按权重不增的顺序重新编号后即为ω1≥ω2≥…≥ωn,下述证明中“每批中工件的编号是连续的”即指按算法A1所得的每批工件是按权重的编号连续的.
证为证明此定理,我们需要从三个方面给以证明.首先需证明每批中工件的编号是连续的.其次还要证明除工件Jn所在的批可能不满外其余的批均为满批.最后需证明该批的序号与该批的完工时间序相一致因而是最优序.其中第二部分的证明过程与[13]的证明类似,在此不再赘述.下面仅就余下两部分给出证明.
首先证明每批中的工件编号是连续的.
若不然,假设ωi>ωj>ωk,且不妨设Ji∈Bi,Jj∈Bj,Jk∈Bi,下面分情况讨论.
1.Bi批在B j批之前加工.交换J j与J k的加工顺序,即将J i与J j放在B i中加工,而J k放在B j中加工,其他工件保持原序.令工件Jx(x=i,j,k)在原先排序和调整后的排序中的完工时间分别记为Cx与C′x.
情形1:若Bi与B j在同一台批处理机上加工,因而批处理机的准备时间相同记为R,不妨设Bi的完工时间为R+xp,Bj的完工时间为R+(x+y)p,x,y为两个大于零的整数,则有
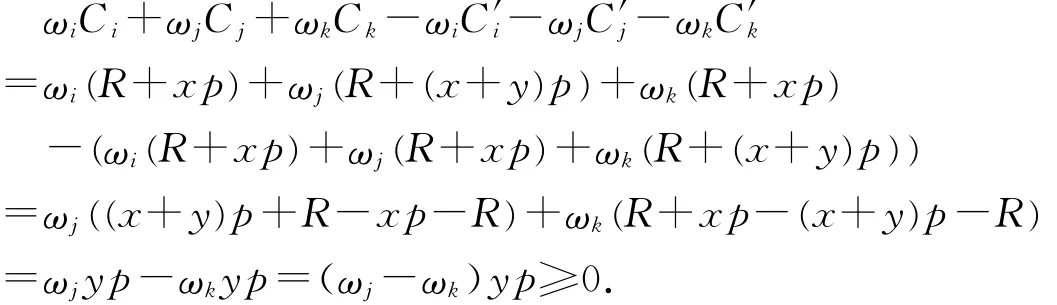
情形2:若Bi与B j不在同一台批处理机上加工,不妨设Bi批在第Mt(t=i,j)台批处理机上加工,且Mt的准备时间为R t(t=i,j),可设Bi的完工时间为R i+xp,Bj的完工时间为R j+yp,其中x,y为两个大于零的整数.因为Bi在B j之前加工,由算法易知Bj的完工时间不会比B i的完工时间早,即Ri+xp≤Rj+yp,则
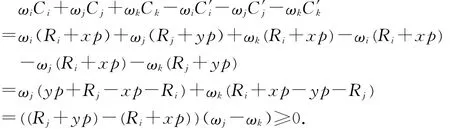
2.Bj批在B i批之前加工.交换Ji与J j的加工顺序,即将Jj与J k放在B i中加工,而Ji放在B j中加工,其他工件保持原序.我们用上述(1)的证明方法同样分两种情形进行讨论.
情形1:若Bi与B j在同一台批处理机上加工,不妨设Bi的完工时间为R+(x+y)p,Bj的完工时间为R+xp,x,y为两个大于零的整数,则易得
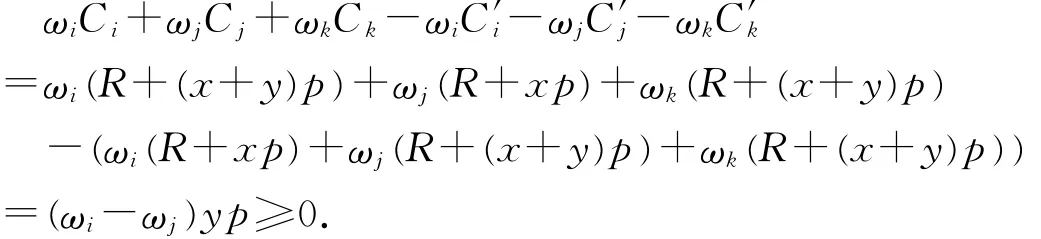
情形2:若Bi与B j不在同一台批处理机上加工,设Bi的完工时间为R i+xp,Bj的完工时间为R j+yp,其中x,y为两个大于零的整数.因为Bj批在B i批之前加工,由算法易知Bi的完工时间不会比B j的完工时间早,即Ri+xp≥Rj+yp,则由条件可得

3.若Bi与B j同时完工,则可以将Ji与J k交换,或者Jj与J k交换,其他工件不变.由于标准加工时间相等,则总的目标函数值是不变的.
通过上述证明可以看出,经过算法调整后的目标函数值显然不劣于调整前的排序,将原先排序中所有满足调整条件的工件均对其进行如上调整,则总的目标函数值不变或者更优,因而每批中的工件的编号是连续的.
由算法A1可知W i≥W j,i>j,而且Bi的完工时间早于B j.所以运用算法A1所得到的排序为最优序.
3 关于Qm,Ri|B,p j=p,rj∈{r1,…,rk}|∑ωjC j的最优算法
在前一部分中,就工件标准加工时间相同且机器带有准备时间的同类机分批排序问题进行了讨论.接下来,将在此基础上进一步考虑工件具有常数个到达时间的问题,即

其中k为常数.同样给出解决这一问题的一个最优算法.


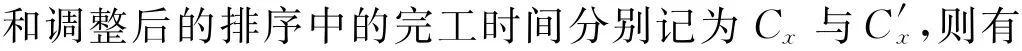


4 结 论
本文首次就排序机器带准备时间的同类机上的分批排序问题进行了研究,给出了两个最优算法A 1和A2,并分别分析了算法的计算复杂性.本文所得结果是在一个相当强的条件下得到的,对于更为一般的情况,该类问题为NP-难的,因此找到更好的近似算法,并分析他们的最差性能比是我们下一步目标.
[1]Uzsoy R,Lee C Y and Martin-Vega L A.A review of production planting and scheduling models in semiconductor industry,Part I:system characteristics,performance evaluation and production planning[J].IIE Transaction,1992,24(4):47-60.
[2]Uzsoy R,Lee C Y and Martin-Vega L A.A review of production planting and scheduling models in semiconductor industry Part II:shop floor control[J].IIE Transaction on Scheduling and Logistics,1994,26(5):44-55.
[3]Zee D J,Vander A,Van Harten and Schuur P C.Dynamic job assignment heuristics for multi-server batch operations-A cost based approach[J].International Journal of Production Research,1997,35(11):3063-3093.
[4]Zee D J,Vander A,Van Harten and Schuur P C.Online scheduling of multi-sever batch operations[J].IIE Transactions,2001,33(7):569-586.
[5]Mathirajan Mand Sivakumar A I.Scheduling of batch processors in semiconductor manufacturing-a review[R].Symposium,National University of Sinngapore,Singapore MIT Alliance,January 2003.
[6]Fanti MP,Maione B P,Iscitelli G and Turchiano B.Heuristic scheduling of jobson a multi-product batch processing machine[J].International Journal of Production Research,34(8):2163-2186.
[7]Brucker P,Ladky G,Hoogeveveen A,Kovalyov H,Potts MY,Tautenhahn C N T and Van de Velde S L.Scheduling a batching machine[J].Journal of Scheduling,1998,1(1):31-54.
[8]Baptiste P.Batching identical jobs[J].A mathematical Methods of Operations Research,2000,22(4):501-524.
[9]Albers S and Brucker P.The complexity of one-machine batching problem[J].Discrete Applied mathematics,1993,47(1):87-107.
[10]Potts C N and Lovalyov MY.Scheduling with batching:a review[J].European Journal of Operational Research 2000,120(2):228-249.
[11]Bruno J,Coffman E G Jr,Sethi R.Scheduling independent tasks to reduce mean finishing time[J].Communications of the ACM,1974,17(7):382-387.
[12]Cheng T C E,Chen Z L,Kovalyov MY and Lin B MT.Parallel-machine batching and scheduling to minimize total completion time[J].IIE Transactions 1996,28(11):953-956.
[13]Deng X,Poon C K and Zhang Y.Approximation algorithms in batch processing[J].Journal of Combinational Optimization,2003,7(3):247-257.
[14]丁际环,等.1|rj∈0,r,B|∑Cj[J].曲阜师范大学学报,2004,30(2):33-35.
[15]苗翠霞,张玉忠.极小加权总完工时间的分批排序问题[J].运筹学学报,2005,9(2):82-86.
[16]张玲玲,等.一种极小化ωj Cj的分批排序问题的算法[J].洛阳大学学报,2005,21(4):43-45.
[17]张玉忠,苗翠霞.复制法及其在分批排序中的应用[J].曲阜师范大学学报,2004.30(2):33-35.
Batch Scheduling Algorithms for Similar Machines with Readiness Time
LIHai-xia1,ZHULu-ning2,ZH AOSheng-ke2
(1.Department of Basic Science,Shandong Water Polytechnic,Rizhao 276826,China;2.Operation Research and Management,Qufu Normal University,Rizhao,276826,China)
This paper investigates sorting problems of two classes of similar machines with readiness time.For problems that have no or constant arrival times and which object functions are minimizing weighted completion time,we present the analysis and proof of two optimal algorithms and their complexities.
batch scheduling;readiness time;FBLW;optimality
O223
A
1672-1454(2011)04-0122-06
2010-09-26
