关于特征函数教学过程中的一点探讨
2013-12-06邢国东赵宣平
邢国东 梁 鑫 赵宣平
(广西师范大学数学科学学院,广西 桂林 541004)
1 引言
由概率论知识可知,随机变量的分布函数全面地描述了随机变量的统计规律,并以分布函数为基础,较详细地讨论了随机变量的数字特征,运算性质等问题。但在这些讨论中,可发现分布函数或分布密度这些工具,有时使用起来并不方便,而概率论中特征函数这一工具,在解决上述和分布有关的问题时,具有极大的优势[1]。按照上述思路,在通常的特征函数的教学过程中,一般先介绍完特征函数的定义以及相关的性质后,而后会介绍特征函数在解决其他有关概率论问题中的应用。但这样的教学过程往往会使特征函数得不到学生们的足够的重视。为此,我们探讨了特征函数在解决其它常见的非概率论的数学问题中也有较为广泛的巧妙的应用。通过上述问题的讲解和分析,我们试图让学生们重视特征函数的学习并激发学生们学习概率论的兴趣,从而提高教学效果和教学质量。
2 特征函数的定义及相关性质[2]
2.1 特征函数的定义
设ξ是任一随机变量,称 ϕ(t) = Eeitξ,-∞ < t<+∞是随机变量ξ的特征函数。
2.2 特征函数的基本性质
性质2.2.1 若 E (Xl)存在 l =1,2,3,Λ ,则随机变量X的特征函数 ϕ(t )可l次求导,且对 1 ≤k≤l ,有 ϕ(k)(0) =ikE(Xk)。
性质2.2.2 随机变量X的特征函数ϕ (t )在(- ∞,+ ∞)上一致连续。
性质2.2.3(逆转公式)设 F(X)和ϕ(t )分别为随机变量X的分布函数和特征函数,则对F(X)的任意两个连续点 x1<x2,
性质2.2.4 ϕ(-t) = ϕ(t ),其中ϕ( t )表示 ϕ(t )的共轭。特别,
大部分教师讲完这些,就算把特征函数的定义和性质讲解完毕。学生们经常感觉到到很抽象,又很枯燥。觉得没有实用性。为了避免给学生留下这种印象,在教学中,我们添加了下面第三部分的内容,使学生觉得特征函数在解决一些数学分析等方面非常简便,从而大大增加了学生们学习的兴趣。
3 特征函数在解决其他常见的非概率论的数学问题中的应用
3.1 在证明恒等式中的应用
我们利用特征函数的定义及其性质,建立概率模型,简便的证明一些恒等式。
例1[3]证明:
证明:由参考文献[3]知,上述恒等式的证明需要利用傅里叶变换计算但过程是非常繁杂的。因此,考虑能否用其他的方法进行计算,经观察,发现,恒等式左边积分的被积函类似于柯西分布的密度函数,而恒等式的右边则类似于柯西分布的特征函数,因此,考虑用特征函数这一工具的相关性质进行证明。


3.2 在求解积分中的应用
数学中求积分,除了利用一些常用的积分公式和分离变量法对积分求解外,我们还可以利用概率论中特征函数的相关性质对积分进行求解。
例2[4]计算积分的值,其中(α∈R)
[4]可知,上述积分求解可利用魏尔斯特拉斯M判别法及含参数反常积分的性质进行计算,也可以通过构造辅助函数和辅助路径,利用留数定理进行计算,但上述方法都非常繁琐,且不易求解。经观察,发现被积函数中e-x2类似于标准正态分布的密度函数,因此考虑利用特征函数的性质求解。

由特征函数的定义及性质2.2.4,得:

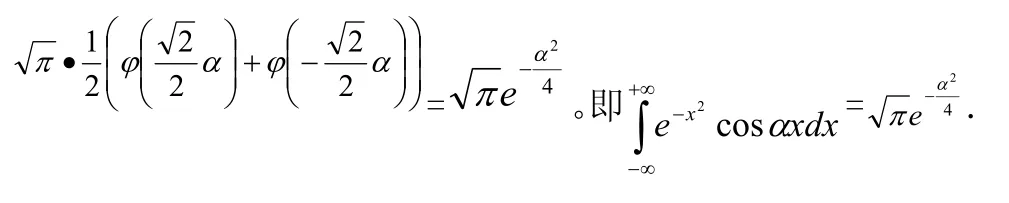
4 结论
通过上述的几个例子的教学,我们发现:学生们自觉地重视特征函数的学习并且学习概率论的兴趣确有增加,教学效果令人满意。
【参 考 文 献】
[1] 魏宗舒.概率论与数理统计[M].高等教育出版社,1999.
[2] 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].高等教育出版社,2004.
[3] 李建林.复变函数与积分变换典型题分析解集[M].西北工业大学出版社,2001:188-190.
[4] 华东师范大学数学系.数学分析(下)[M].高等教育出版社,2005:187-188.
