氮掺杂(1120)ZnO薄膜磁性质研究*

李明标张天羡史力斌

氮掺杂(1120)ZnO薄膜磁性质研究*

李明标 张天羡 史力斌

(渤海大学数理学院，锦州121013)
(2010年10月22日收到;2010年12月7日收到修改稿)

采用基于密度泛函理论(DFT)和局域密度近似(LDA)的第一性原理分析了氮掺杂(1120)ZnO薄膜的磁性质．首先，研究了一个N原子掺杂ZnO薄膜的磁性质，结果表明N 2p，O 2p和Zn 3d发生自发自旋极化．其次，研究了二个N原子掺杂ZnO薄膜的磁性质，9个不同几何结构的计算结果表明N原子之间具有FM耦合稳定性，而且具体分析了N掺杂ZnO铁磁稳定性的产生原因．最后，讨论了氮掺杂ZnO磁交换系数和居里温度．计算结果表明N掺杂(1120)ZnO薄膜具有弱铁磁性．

第一性原理，半导体，铁磁性

PACS:75．50．Pa，71．55．Gs，75．30．Hx

1.引言

稀磁半导体(DMS)由于同时具有半导体材料的传导特性和磁性材料的存储特征，在新型自旋电子器件中具有潜在应用前景，因此得到了广泛重视［1］．特别是寻找具有较高居里温度DMS成为了人们关注的焦点．尽管人们已经在Ⅲ-Ⅴ族稀磁半导体上做了大量研究工作，但由于它们的居里温度较低，这使其无法投入实际应用［2，3］．目前，人们不得不集中精力去寻找具有更高居里温度的新型稀磁半导体．

Zn O是一种六角结构的Ⅱ-Ⅵ族直接带隙半导体(室温下带隙为3.37 eV)，由于它具有低介电常数、大光电耦合系数、高化学稳定性、高激子结合能(高达60 m eV)及优良的光电、压电特性，因此在发光二极管、光电探测器、表面声波器件及太阳能电池等领域有广泛的应用前景［4，5］．ZnO半导体的稀磁特性也引起了高度重视．人们已经对过渡金属掺杂的ZnO做了大量研究工作［6—8］．过渡金属掺杂的ZnO中过渡金属团簇和第二相等问题限制了其应用．解决这些问题的一个有效办法是在ZnO中掺杂非过渡金属元素．近来，在C或N掺杂的Zn O中发现了铁磁性质［9—12］．非过渡金属掺杂ZnO的铁磁性质不同于过渡金属掺杂的ZnO．首先，C或N原子在离子态没有不成对的自旋．其次，在C或N的2 p轨道比过渡金属的d轨道具有更强的非局域特征．因此，C或N掺杂ZnO可能具有长程铁磁耦合的特点．再次，对于C或N的2 p轨道来说，自旋和轨道之间的相互作用是弱的．尽管，目前对C或N掺杂的ZnO铁磁性做了一些研究工作．但对C或N掺杂ZnO铁磁性产生的原因还没有彻底弄清．鉴于以上这些原因，本文利用第一性原理研究了N掺杂(1120)Zn O薄膜中的铁磁性质，并且对其磁耦合系数和居里温度进行了讨论．我们期望我们的工作能为这类新型稀磁半导体的应用提供一些参考．

2.计算方法

本文采用基于密度泛函理论和平面波赝势技术的CASTEP程序对N掺杂Zn O铁磁性质进行了计算［13］．交换关联函数采用Ceperley，Alder，Perdew和Zunger(CA-PZ)的局域密度近似(LDA)［14，15］．另外，我们采用超软赝势来描述离子实与价电子之间的相互作用．选取Zn，O，N原子价电子组态分别为3 d104s2，2 s22 p4，2s22 p3，其他轨道电子视为芯电子来进行计算．ZnO在常温和常压下稳定结构是纤锌矿结构，它的晶格常数是a=3.246，c=5.200［16］．因此本文计算是在B4相ZnO上进行的．

图1 ZnO薄膜示意图(图中浅色大原子表示O原子，深色小原子表示Zn原子)

通过在ZnO超晶胞中沿(1120)方向切割可以获得11层ZnO平板，这平板被一定厚度的真空层隔开，由此我们获得了Zn O薄膜结构(见图1)．在ZnO薄膜结构中包含36个Zn原子和36个O原子．这种薄膜结构考虑了表面效应．为了研究N掺杂ZnO的自旋极化，我们分别用一个N和两个N取代ZnO薄膜中O，使得N浓度分别为2.8%和5.6%．为了研究N掺杂ZnO磁性质，我们计算了包含一个N原子ZnO超晶胞在自旋极化和非自旋极化下的系统能量．另外，为了研究N原子之间的磁相互作用，我们也计算了包含二个N原子ZnO超晶胞在铁磁(FM)和反铁磁(AFM)态的能量．为了保证计算的精度，我们对截断能和真空层厚度进行了认真核查，计算中对Brillouin区的积分计算使用了Monkhorst-Pack方案，K点选取为3×3×2．从图2可以看出当Ecut=400 eV时总能几乎不再发生变化，因此平面波截断能最终设置为400 eV．在Ecut= 400 eV时，晶格常数为a=3.184和c=5.149，略小于实验值．计算发现当真空层厚度达到10时，系统总能基本不发生变化，因此我们把Zn O薄膜的真空层厚度设为10．本文对晶格常数和内坐标同时进行几何优化，所有性质的计算都是在几何优化条件下进行的．模型优化采用了BFGS算法．

图2 ZnO晶格常数和系统能量随截断能的变化

3.结果与讨论

3.1.N掺杂ZnO的自发自旋极化

为了研究N掺杂ZnO薄膜铁磁性质起源，我们首先在构建的(1120)Zn O薄膜中引入一个N原子．在原子充分弛豫的情况下计算了10个不同的几何结构在自旋极化和非自旋极化下的能量，计算结果可见表1．为了对不同几何结构的能量进行了比较，我们把几何结构4在自旋极化下能量作为参考能量．从表1可以看出结构3和结构4具有更低的能量，这表明N原子将优先取代薄膜表面下第二层O原子．这是因为O原子得到二个电子便可以形成稳定结构，N原子则需要三个电子才能形成稳定的结构，而薄膜表面具有断键特征，因此N原子取代薄膜表面O原子不利于形成稳定结构．又由于N离子半径(1.46)大于O离子半径(1.38)［17］，N取代O将引发晶格畸变．N离子从薄膜表面深入到薄膜内部，引发晶格畸变将越发严重，导致系统能量升高．因此从N原子成键和晶格畸变角度分析N取代薄膜表面第二层O更有利于结构稳定．先前，Wang等［18］研究了过渡金属元素掺杂(1120)Zn O薄膜的铁磁性质，发现过渡金属原子Cr，Fe，Co和Ni优先占据薄膜表面．这是因为薄膜表面的断键特征对过渡金属原子结构稳定性影响不大，而过渡金属离子半径不同于鋅离子半径，取代薄膜表面以下锌离子将导致更大的晶格畸变，因此对于过渡金属离子在薄膜表面更有利于结构稳定．从表1也可以看出系统在自旋极化下能量小于系统在非自旋极化下能量．因此N掺杂的ZnO可以产生自发自旋极化．

表1 在(1120)Zn36NO35薄膜中N原子在不同位置时自旋极化下能量Espin，非自旋极化下能量E0，N原子最近邻Zn磁矩MZn，N原子次近邻O磁矩MO，居里温度Tc1和磁耦合系数JN-O．几何结构4在自旋极化下能量作为参考能量，且ΔE1=Espin－E0．小括号里数字表示发生自旋极化的近邻Zn和次近邻O离子个数

图3(1120)Zn36NO35薄膜中几何结构4下的自旋分波态密度(正值表示主自旋态，负值表示小自旋态)

图3 显示了系统在自旋极化基态(几何结构4)的自旋分波态密度．图中竖直点线表示费米能量．从图3可以看出在费米能级处N 2p电子态几乎100%自旋极化．在费米能级处的电子态属于N 2 p的小自旋态．N 2 p主要和次近邻O 2p发生杂化，导致次近邻O 2 p态密度在费米能级附发生了自旋极化．但其他的O并不发生自旋极化．图3也可以看出N近邻Zn 3d的自旋也发生了部分极化．图4显示了N掺杂(1120)ZnO薄膜在自旋极化下的自旋电荷密度．对于几何结构1，N原子取代了ZnO薄膜表面的O，由于表面结构存在断键特征，从图4(a)可以看出N自旋电荷密度沿表面很快衰减为零．几何结构4与几何结构1相比，发生自旋极化的最近邻Zn和次近邻O原子个数增多．磁矩的计算结果也显示N掺杂(1120)ZnO薄膜磁矩主要来源于N 2p，部分来源于O 2p，少量来源于Zn 3d(具体见表1)．

图4 (1120)Zn36NO35薄膜的自旋电荷密度图(大浅色球表示O原子，小暗球表示Zn原子，大暗球表示N原子)(a)表示几何结构1的自旋电荷密度图;(b)表示几何结构4的自旋电荷密度图

3.2.N离子间FM耦合

为了分析N掺杂Zn O薄膜中N原子之间的FM耦合，我们也计算了两个N原子掺杂ZnO薄膜在FM和AFM耦合的能量．表2显示了9个不同的几何结构的计算结果．从FM和AFM态能量的差(ΔE2=EFM－EAFM)，我们能估计那个态是更稳定的，负的ΔE表示FM态更稳定，正的ΔE表示AFM态更稳定．表2的计算结果显示N原子间FM态比AFM态更稳定．对于几何结构4，N原子间的距离为9.856，计算结果显示它在FM态的能量最低，并且ΔE2=－111 meV．从表2也可以看出N原子间具有长程铁磁耦合的特点，这与文献［12］报道是一致的．

现给出一个清晰的物理图像去描述N掺杂ZnO中铁磁性起源．在B4相结构中，近似认为N原子处于四面体晶体场(Td)中［19］．这Td晶体场劈裂N成低能s态和高能三重p态．假设晶体场中每个N原子从Zn原子中获得两个电子，图5显示了N能级分布．图5(a)和(b)分别显示了N原子之间FM和AFM耦合．对于FM耦合，所有主自旋(s1，p1)和小自旋态(s2)被电子完全占据，而小自旋(p2)态被电子部分占据，费米能级附近态密度主要来源于小自旋p2态，这符合态密度计算结果(见图3)．对于电子完全占据的主自旋s1，p1和小自旋s2，FM耦合使得一个能级被抬高，而另一个能级被降低相同的高度．能级被抬高的电子数等于能级被降低的电子数，系统没有能量释放．而在小自旋p2之间的FM耦合，根据能量最低原理，电子优先占据低能态，因此占据低能态的电子数大于占据高能态的电子数，导致系统有能量释放．对于AFM耦合，一个N离子的p1(s1)主自旋与另一个N离子的p2(s2)小自旋进行耦合，系统没有净能量释放．因此对于N掺杂的ZnO在FM态更有利于系统稳定．这可以解释为何N掺杂ZnO拥有铁磁性稳定性．

表2 在(1120)Zn36N2O34薄膜中9个不同几何结构在FM和AFM态能量，N离子磁矩MN，居里温度Tc2，N离子间磁性耦合系数JN-N和N原子之间距离．几何结构4中FM态的能量作为参考能量，且ΔE2=EFM－EAFM

3.3.N掺杂ZnO薄膜中磁交换系数和居里转变温度

在晶体中，如果离子间存在磁相互作用，那么Heisenberg Hamiltonian方程可以写为［20］

其中Si是磁性离子的自旋，Je是第i个离子与第j个离子的交换积分，也称为磁性耦合系数．因为Je取决于两个离子轨道之间的重叠，在晶体中通常只考虑近邻离子之间的交换能，交换能的作用也相当于一个有效场

其中z是参考离子的近邻数目，gs是朗德因子，μB是玻尔磁子，μ是磁矩．假设磁体单位体积内有N个离子，尽管磁体内各离子磁矩可以取不同的值，但平均值可以写为，M是磁化强度，由此可以获得平均场为

其中λ是平均场常数，如果磁体内的磁矩主要来源于离子的自旋磁矩，磁化强度可以写为

其中

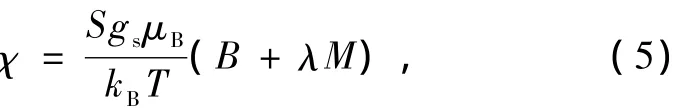
图5 N离子间能级间耦合示意图(a)表示N离子之间的FM耦合示意图;(b)表示N离子间AFM耦合示意图

方程(5)中kB是玻尔兹曼常数．如果在方程(4)和 (5)中把χ当做自变量，那么在T=Tc时，方程(4)和(5)的斜率应相同，由此得

在平均场近似下，如果把方程(3)中的λ代入方程(6)，那么铁磁性居里温度

μs为离子的自旋磁矩，如果磁矩由多种离子共同贡献，那么离子之间的磁相互作用可以分为同种离子之间的磁相互作用和异种离子之间的磁相互作用．对于异种离子之间的磁性耦合具体可以分为N-Zn和N-O离子之间的耦合，这类耦合中一种耦合发生在N的2p和Zn的3d轨道上，因此磁性耦合系数可写为JN－Zn，另一种耦合发生在N 2 p和O 2 p轨道上，磁性耦合系数可写为JN－O．在N掺杂ZnO中与异种离子间磁相互作用相联系的居里温度可表示为JN－Zn表示参考离子N与最近邻Zn离子之间的耦合系数，JN－O表示参考离子N与次近邻O离子之间的耦合系数．μN是N离子的自旋磁矩，μZn和μO分别表示N离子最近邻Zn和次近邻O离子磁矩．z1和z2分别表示与N离子耦合的最近邻Zn和次近邻O离子个数．因为N掺杂ZnO薄膜中磁矩主要由N和次近邻O决定，N最近邻Zn磁矩很小，而且在N掺杂ZnO薄膜中发生自旋极化Zn离子个数也远小于O离子个数．因此我们认为N掺杂ZnO中异种离子之间的磁相互作用主要由N-O相互作用决定．图3态密度图谱显示N 2 p态和次近邻O 2 p态发生杂化，并且他们在费米能级附近的态密度发生自旋极化，而最近邻Zn 3 d态在费米能级处态密度很小，仅有少量极化．态密度的结果也证实异种离子之间的磁相互作用主要由N-O作用决定．因此与异种离子磁相互作用相联系的居里温度可近似为

ΔE1(A)=Espin－E0，Espin是一个N原子(用编号A表示)掺杂ZnO自旋极化下的能量，E0是非自旋极化系统的能量．对于N-N同种离子间的耦合，磁性耦合系数可以写为JN－N．那么与同种离子间磁相互作用相联系的居里温度可表示为［21］:

其中，μs表示N离子磁矩．ΔE2(A，A')=EFMEAFM表示在两个N原子(编号分别为A，A')掺杂ZnO超晶胞中FM与AFM态能量差．之前的一些理论只能对同种原子之间的磁相互作用给出理论描述，对于异种离子之间的磁相互作用没有做出具体的说明［22，23］．但实际的磁性半导体中往往同时存在同种离子间耦合与异种离子间耦合，我们的理论模型包含了同种、异种离子磁耦合特征，所得的结论更具有普遍意义．

表1，2分别给出了计算的异种离子之间的磁耦合系数JN－O和同种原子间的有磁耦合系数JN－N．从表中我们可以看出对于不同的几何结构，磁耦合系数有所不同．氮掺杂(1120)ZnO薄膜具有自发自旋极化特征，而且具有铁磁稳定性，因此耦合系数均为正值．先前，Wu等［24］研究了Zn1－xCoxO稀磁半导体的磁耦合系数，计算结果表明，磁耦合系数J＜0.1 eV，远小于我们的结果，这是因为过渡金属元素Co的磁矩(～3μB)远大于N，O的磁矩(见表1)．(9)和(10)式表明磁耦合系数和磁矩的平方成反比．因此我们的结果是合理的．

本文利用Heisenberg的局域电子模型来处理N掺杂ZnO薄膜中磁交换系数和居里温度，该模型适合分析最近邻N离子之间以及N与次近邻的O离子之间的磁相互作用．表1给出了N与次近邻O离子之间的磁相互作用相联系的居里温度(Tc1)．在表1中共有10种几何结构，其中几何结构3，4能量较低，是FM基态，因此几何结构3，4得出的结果更能反映实际情况．为了分析N原子之间的磁性耦合，我们也分析了两个N原子掺杂ZnO磁性质．由于本文的模型只适合分析最近邻N原子之间的相互作用．因此表2中我们只给出了最近邻几何结构7和8的结果．由于结构7和8的能量较高，该结构很难在实际样品中形成，计算得到的Tc2并不能反应样品的实际情况．因此该模型未能对N离子之间的磁性耦合作出有效的描述．由于N，O磁矩较小，暗示N掺杂ZnO薄膜具有弱铁磁特性．

ZnO薄膜结构中由于真空层的存在，考虑了表面效应．这使得N掺杂ZnO薄膜与块体材料中的磁性质有所不同．先前，N掺杂ZnO晶体的磁性质已被研究［25］，研究发现N在ZnO晶体中具有团簇趋势，而我们在氮掺杂(1120)ZnO薄膜并没有发现N离子的团簇趋势．Shen等［12］利用第一性原理分析了N掺杂ZnO晶体的磁性质，计算N掺杂ZnO离子磁矩，结果表明每个N离子引入系统，将带来1.0μB磁矩，其中大约0.4μB来源于N离子，其中0.4μB来源于次近邻O离子，并且有大约0.1μB来源于最近邻Zn离子．而我们对薄膜结构的计算结果表明，N，Zn，O离子磁矩随N位置的不同而发生变化(见表1)．对于N掺杂ZnO晶体研究表明N和O之间的相互作用对其铁磁性有着重要的影响，这与我们对N掺杂(1120)ZnO薄膜的研究结果相一致．

4.结论

一个N原子掺杂的ZnO薄膜显示出自旋极化现象，这自旋极化来源于N 2p，O 2 p和Zn 3 d．对于两个N原子掺杂的Zn O薄膜，N原子之间显现FM稳定性，这FM稳定性可以通过N原子能级之间的耦合进行解释，并且这FM耦合具有长程的特征．利用Heisenberg的局域电子模型分析了磁交换系数和居里转变温度，因为磁交换系数与原子磁矩的平方成反比，N，O，Zn离子磁矩相对较小，导致N掺杂的ZnO磁交换系数较大．该模型能分析N与次近邻O离子之间的磁相互作用，但未能有效分析N原子之间的FM耦合．N掺杂的ZnO薄膜中由于磁矩较小，因此该薄膜显示弱铁磁特征．

本工作在计算中得到了西南大学物理科学与技术学院袁宏宽老师的帮助，在此我们表示衷心的感谢．

［1］Pan F，Song C，Liu X J，Yang Y C，Zeng F，2008 Materials Science and Engineering R 62 1

［2］Schallenberg T，Munekata H 2006 Appl．Phys．Lett．89 042507

［3］Nazmul A M，Sugahara S，Tanaka M 2003 Phys．Rev．B 67 241308

［4］Shi L B，Kang L，Jin J W，Chi F 2009 Chin Phys．B 18 4418

［5］Cheng X W，Li X，Gao Y L，Yu Z，Long X，Liu Y 2009 Acta Phys．Sin．58 2018(in Chinese)［程兴旺、李祥、高院玲、于宙、龙雪、刘颖2009物理学报59 2018］

［6］Liu X C，Lu Z H，Zhang F M 2010 Chin Phys．B 19 027502

［7］Lu Z L，Zou W Q，Xu M X，Zhang F M 2010 Chin．Phys．B 19 056101

［8］Shi H L，Duan Y F 2008 J．Appl．Phys．103 073903

［9］Pan H，Yi J B，Shen L，Wu R Q，Yang J H，Lin J Y，Feng Y P，Ding J，Van L H，Yin J H 2007 Phys．Rev．Lett．99 127201

［10］Zhou S Q，Xu Q Y，Potzger K 2008 Appl．Phys．Lett．93 232507

［11］Herng T S，Lau S P，Wang L，Zhao B C，Yu S F，Tanemura M，Akaike A 2009 Appl．Phys．Lett．95 012505

［12］Shen L，Wu R Q，Pan H，Peng G W，Yang M，Sha Z D，Feng Y P 2008 Phys．Rev B 78 073306

［13］Payne M C，Teter M P，Allan D C，Arias T A，Joannopoulos J D 1992 Rev．Mod．Phys．64 1045

［14］Ceperley D M，Alder B J 1980 Phys．Rev．Lett．45 566

［15］Perdew J P，Zunger A 1981 Phys．Rev．B 23 5048

［16］Yang Y，Qi J，Zhang Y，Liao Q，Tang L，Qin Z 2008 Appl．Phys．Lett．92 183117

［17］Assadi M H N，Zhang Y B，Li S 2009 J．Appl．Phys．105 043906

［18］Wang Q，Sun Q，Jena P，Kawazoe Y 2009 Phys．Rev．B 79 115407

［19］WaLsh A，Silva J L F，Wei S H 2008 Phys．Rev．Lett．100 256401

［20］Dev P，Xue Y and Zhang P 2008 Phys．Rev．Lett．100 117204

［21］Turek I，Kudrnovsk J，Bihlmayer G，Blugel S 2003 J．Phys．: Condens．Matter 15 2771

［22］Kurz P，Bihlmayer G，Blugel S 2002 J．Phys．:Condens．Matter 14 6353

［23］Bergqvist L，Kudrnovsky J，Drchal V，Korzhavyi P，Turek I 2004 Phys．Rev．Lett．93 137202

［24］Wu Q Y，Chen Z G，Wu R，Xu G G，Huang Z G，Zhang F M，Du Y W 2007 Solid State Communciations 142 242

［25］Shi L B，Jin J W，Xu C Y 2010 Modern Physics Letters B 2171

PACS:75．50．Pa，71．55．Gs，75．30．Hx

*Project supported by the Science Foundation from Education Department of Liaoning Province，China(Grant No．L2010003)．

E-mail:slb0813@sohu．com

Magnetic properties of N-doped(1120)ZnO thin films*

Li Ming-Biao Zhang Tian-Xian Shi Li-Bin
(School of Mathematics and Physics，Bohai University，Jinzhou 121013，China)
(Received 22 October 2010;revised manuscript received 7 December 2010)

By using the first principles method based on the density function theory(DFT)and the local density approximation (LDA)，we study the ferromagnetic properties in N-doped(112 0)ZnO thin films．Magnetic properties in one-N-doped ZnO are investigated．The spontaneous spin polarization comes from N 2p，O 2 p and Zn 3 d．Magnetic properties in two-N-doped Zn O are also investigated．The calculated results show that ferromagnetism(FM)coupling between N atoms is more energetically favorable for nine geometrically distinct configurations．The origin of the FM state in N-doped ZnO is also discussed by analyzing the coupling of N levels．Finally，the magnetic exchange coefficient and the Curie temperature are discussed．The result indicates that N-doped ZnO thin films show weak FM properties．

the first principles，semiconductor，ferromagnetism

*辽宁省教育厅项目(批准号:L2010003)资助的课题．

．E-mail:slb0813@sohu．com