Ba0.5Sr0.5TiO3有序构型的第一性原理研究*
2011-11-02何建平吕文中汪小红
何建平吕文中汪小红
Ba0.5Sr0.5TiO3有序构型的第一性原理研究*
何建平 吕文中汪小红
(华中科技大学电子科学与技术系,电子信息功能材料教育部重点实验室(B类),武汉430074)
(2010年11月17日收到;2010年12月11日收到修改稿)
采用第一性原理计算了Ba0.5Sr0.5TiO3三种有序构型的晶格结构和对应的电子结构,晶格结构的详细分析结果表明BST{100}有序构型为四方相,Ti-O八面体中Ti原子和Ba-Sr平面上的O原子沿[100]方向分别偏心位移0.040和0.065,八面体畸变导致反平行自发极化出现,构型处于反铁电态.BST{110}构型也是四方相,并且(110)和(110)面上的O原子存在0.029偏心移动,但Ti原子仍位于Ti-O八面体中心,构型处于顺电态.而BST {111}构型为立方相,其Ti-O八面体高度对称无畸变,构型为顺电态.态密度结果显示Ti3d和O 2p轨道的杂化作用对BST钙钛矿晶体中铁电性的产生起着至关重要的作用,计算结果的综合分析表明A位的局部有序性会导致无序结构BST固溶体的结构相变.
钛酸锶钡,第一性原理,有序结构,铁电性
PACS:71.15.Mb,71.15.-m,77.80.-e,77.22.Ej
1.引言
钙钛矿型铁电体作为一种典型铁电体,在实际应用和凝聚态物理的基础研究方面受到广泛关注和重视而成为一个重要的热门研究领域.其中,由BaTiO3和SrTiO3形成的一种连续可调固溶体——钛酸锶钡(BaxSr1-xTiO3,BST)备受关注,其介电常数在外加直流偏置电场作用下呈现显著的介电非线性,这一特性使BST能够应用于微波调谐器件,如调制器、滤波器和移相器等方面[1—5].此类实验工作让我们对铁电体的电学特性和铁电特性有了深入了解,相关机理研究也逐渐使铁电体的特性全面地展现出来.
近20年来,随着密度泛函理论的发展,第一性原理方法开始应用在钙钛矿铁电体的微观理论研究中,从1992年Cohen指出钙钛矿铁电体中Ti 3 d和O 2p轨道之间的杂化作用是晶体铁电性产生的重要原因开始[6],经过10多年进一步广泛和深入的研究,现在已经能够对BaTiO3,SrTiO3和PbTiO3等单一组分钙钛矿铁电体的铁电性、表面效应等做出解释,并能做出一些预测分析[7—13]和掺杂计算研究[14,15].实际中所需要能够应用的大多为固溶体类多组分铁电材料,在这类钙钛矿材料的晶格结构中的同一位置通常被两种或两种以上的原子所占据,因此对于这种结构的第一性原理研究就成为一个热点和难点.文献[16]和[17]分别对A位复合型Pb1-xCaxTiO3和B位复合型PbMg1/3Nb2/3O3进行了第一性原理计算研究,文献[18]通过对总能量的计算研究了BaxSr1-xTiO3的结构,文献[19]建立了一个Ba和Sr均匀间隔分布结构模型对立方相Ba0.5Sr0.5TiO3的结构稳定性和电子结构进行了计算,而文献[20]则使用了一个[001]方向的叠加套构模型对Ba0.5Sr0.5TiO3的电子结构和光学性质进行了理论研究.对于Ba0.5Sr0.5TiO3中A位原子有序构型的详细计算,以及不同有序性对BST铁电性的影响等,目前未见有文献报道.本文将建立三种有序构型对Ba0.5Sr0.5TiO3进行结构上的第一性原理计算分析,并深入了解不同A位有序性和BST铁电性之间的关系及其微观机理.
2.计算模型和方法
在Ba0.5Sr0.5TiO3固溶体中,Ba原子和Sr原子随机分布于A位,为了便于进行第一性原理计算,我们让Ba原子或Sr原子分别沿垂直于[100],[110]和[111]方向的面进行分布,建立如图1所示的BST{100},BST{110}和BST{111}三种有序构型,图中原子为Ba和Sr,为了简化图形,Ti和O原子未画出.本文的计算采用基于密度泛函理论的第一性原理CASTEP软件包[21],价电子和离子实之间的相互作用使用超软赝势(ultrasoft vanderbilt pseudopotentials,USP)[22]来描述,Ba,Sr,Ti和O原子的价电子组态分别为5 s25p66 s2,4 s24 p65 s2, 3s23 p63d24 s2和2 s22p4,各原子的其他电子作为芯电子处理.选择广义梯度近似(generalized gradient approximation,GGA)[23]下的PBE泛函[24]来处理电子交换关联项,平面波截断能取400 eV,布里渊区积分应用Monkhorst-Pack方案[25],设置自洽计算精度为5.0×10-7eV/atom.首先对上述三种有序构型进行几何结构优化,找到各自能量最低的稳定结构状态,然后在稳定构型的基础上进行电子结构的计算.
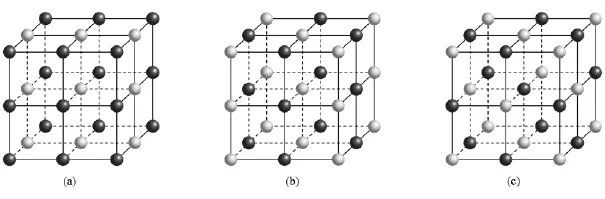
图1 Ba0.5Sr0.5TiO3的三种有序构型(a)BST{100};(b)BST{110};(c)BST{111}
3.结果与讨论
3.1.晶格结构和布居分析
几何结构优化后得到的BST{100}和BST {110}构型为四方相,晶胞结构如图2所示(O原子未画出),BST{111}构型为立方相.观察仅包含一个Ti-O八面体的格子,在BST{100}晶胞中,晶格在[100]方向上收缩0.001,而BST{110}的晶格在[001]方向上收缩0.006,即后者具有相对更大的晶格畸变.表1列出了计算获得的三种构型的晶格常数(按照包含一个Ti-O八面体的格子计算),数值上依次增大,介于BaTiO3和SrTiO3晶格常数之间,与Ba0.5Sr0.5TiO3实验值的相对偏差小于1.5%,精度满足要求.
为了进一步了解三种构型的详细晶格结构和原子间的相互作用,将各构型中的键长和相应的Mulliken布居数据列于表2,立方相BaTiO3和SrTiO3也列在表中.对BST{100}构型,O1,O2和O3分别对应晶胞中三种不同位置的O原子,见图2 (a);而BST{110}构型的晶胞中存在O1和O2两种不同位置的O原子,见图2(b).

图2 BST{100}和BST{110}构型几何优化后的晶胞结构(a)BST{100};(b)BST{110}
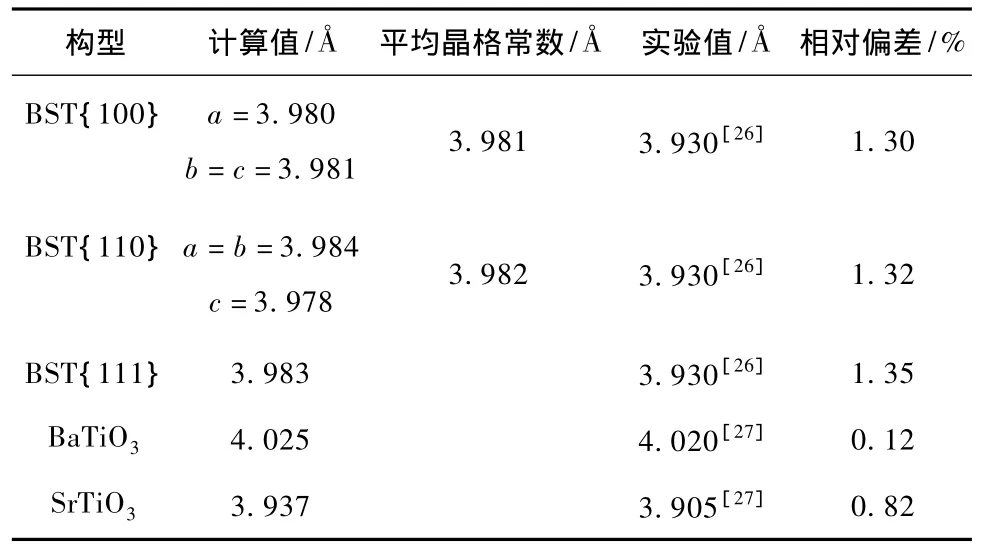
表1 计算得到的晶格常数
从O―Ti键长可知在BST{100}构型中,Ti原子沿[100]方向靠近Sr平面,偏离Ti-O八面体中心移动0.040;而BST{110}构型中的Ti原子没有偏心位移.另外,在BST{100}构型中,O2原子沿[100]方向偏离Ba-Sr面心向Sr平面移动0.065,BST{110}构型中的O2原子则在(110)和(110)面内偏离Ba-Sr面心向Sr所在轴线移动0.029.由此可见,尽管BST{100}构型的晶格相比BST{110}的晶格收缩小,但其有着更大的Ti-O八面体畸变.出现这样的情况,主要是因为在Ba0.5Sr0.5TiO3中,Ba2+离子半径比Sr2+离子半径大,Ti4+和O2-离子受到一定的挤压而产生朝向Sr的偏心位移.在BST {100}构型中,Sr对O2的吸引作用随着距离的靠近而增强,导致O2进一步向Sr平面移动,偏心位移增大;Ti虽然由于被挤压而靠近Sr平面,但是两者之间的斥力也随之增大,使得Ti不能继续向Sr平面移动,同时Ti-O间的相互作用对O2向Sr平面的位移产生牵制,阻止O2偏心位移的增大.O2和Ti向Sr的偏心位移使得Ba受到作用力减少,为了维持体系的平衡和降低体系能量,晶格收缩,另外由于Ba2+离子半径较Sr2+离子半径大,晶格在[100]方向上的收缩比另外两个方向略多.而在BST{110}构型中,O1和Ti处在一个对称的位置,受到各方向均衡的作用而无偏心位移,而O2在(110)和(110)面内偏离Ba-Sr面心向Sr所在轴线移动.同上,Ti-O间的相互作用将阻止O2偏心位移的增大,由于Ti没有偏心位移,BST{110}构型中的O2偏心位移比BST{100}构型的小,这也导致BST{110}构型晶格在[001]方向上收缩较其他方向多.
在BST{100}构型中形成的Ti-O八面体畸变将导致[100]方向出现电偶极矩,从而出现自发极化,由于这种自发极化在[100]方向上成对出现,而且极化方向相反,所以对外仍不会出现宏观极化而呈现铁电性.在外加电场作用下,这种自发极化对会转向分开,从而显示出铁电性,这符合反铁电体的特征,因此以BST{100}构型状态存在的Ba0.5Sr0.5TiO3处于反铁电态.另外,尽管BST{110}构型为四方相且O2有偏心位移,但是因为Ti不存在偏心位移,以及Ti-O八面体仍然具有很高的对称性,所以该构型中没有出现自发极化而处于顺电态.而BST {111}构型为高对称性的立方相,不存在O和Ti的偏心位移,也为顺电态.同时,我们计算得到了各构型的能量,BST{100}构型的能量比BST{110}和BST{111}构型的能量分别低3.5×10-3eV/atom和6.2×10-3eV/atom,因此Ba0.5Sr0.5TiO3中倾向于出现BST{100}构型.
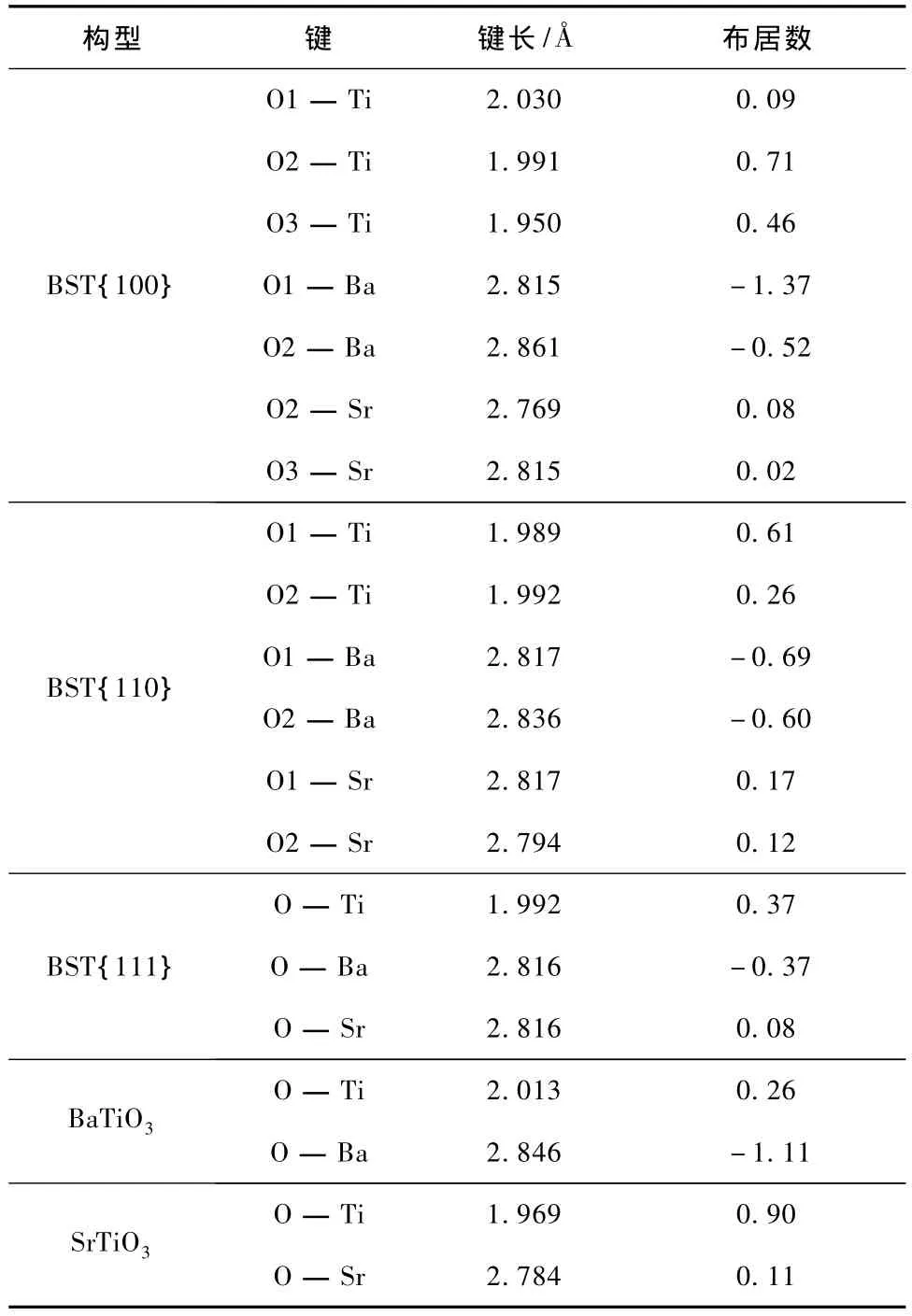
表2 Ba0.5Sr0.5TiO3各构型中的键长和Mulliken布居数
表2中的Mulliken布居数表明在Ba0.5Sr0.5TiO3各构型中,O和Ti之间形成的键具有共价性,O和Ba之间形成的是反键,而O和Sr之间形成的键是具有弱共价性的离子键.O—Ba和O—Sr这种成键特点在文献[11]和文献[28]也分别有所体现.纵观各构型(包括BaTiO3和SrTiO3)的布居数据可以发现,同一类键(如O―Ti键)的键长和反映键强度的布居数并不表现为线性变化关系,即键长越短,键的强度越高.布局数的这种不明显规律性变化,可能是因为体系的组成不同以及原子位置种类的多样化.
3.2.态密度分析
图3是Ba0.5Sr0.5TiO3三种有序构型以及BaTiO3和SrTiO3中原子各轨道的分态密度图.由图3(a)和(b)可以看出,除了BST{111}和BaTiO3中的Ba 2 p轨道在约-10 eV处的态密度特征峰值以及SrTiO3中的Sr 2 p轨道在约-14.5 eV处的特征峰值相对其他同样轨道的特征峰值略有降低外,各结构中的Ba和Sr的态密度基本上没有变化.观察图3(a),(b)和(d)发现Ba-O和Sr-O的轨道杂化作用主要是在-17.5 eV到-15 eV能量区间,以及约-10 eV和约-14.5 eV处,并且后者的作用相对强烈.在约-10 eV处Ba 2p和O 2 s以及约-14.5 eV处Sr 2p和O 2 s的轨道杂化,可能是Mulliken布居分析中O—Ba和O—Sr成键类型不同的原因所在.
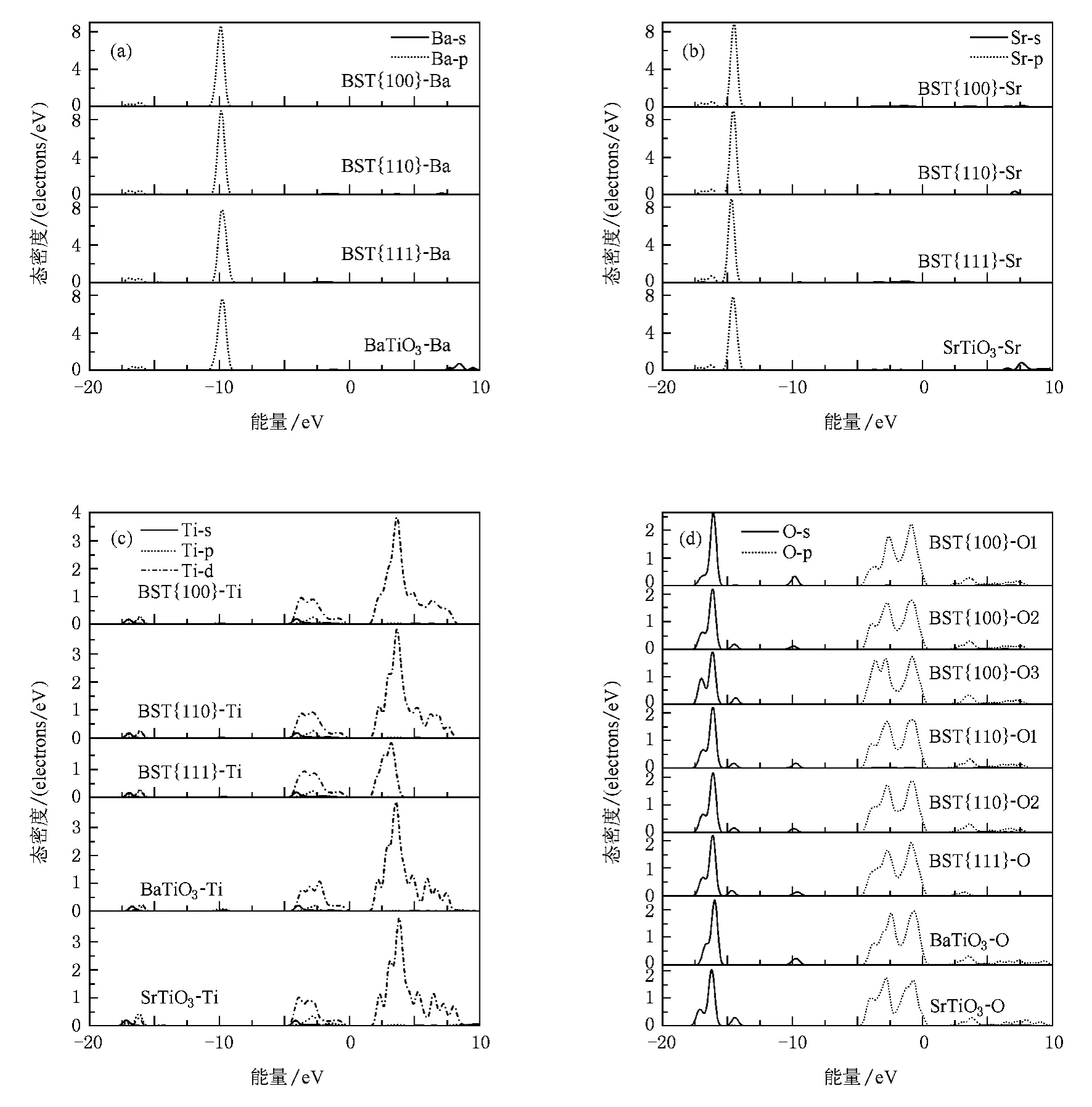
图3 各原子的分态密度(a)Ba;(b)Sr;(c)Ti;(d)O
由于Ti-O八面体这种特殊结构的存在,使得三种构型中Ti和O的分态密度具有BaTiO3和SrTiO3中Ti和O的分态密度的综合特征,不难看出在-5 eV到10 eV之间的轨道杂化作用主要是由Ti 3 d和O 2p轨道贡献.BST{111}中0 eV到10 eV区间的Ti 3d轨道的态密度被压缩在2 eV到5 eV范围内,且峰值只有其他Ti 3d轨道的一半,这使得该Ti和O之间的轨道杂化作用被削弱,O―Ti键强度降低,将有利于BST{111}构型顺电态的维持.对比图3(d)中O的态密度可以看到BST{100}构型中O的态密度不仅和其他结构中O的态密度有着明显不同,自身的三种位置O的态密度也存在显著差异.BST{100}-O1和BST{100}-O3的2 s轨道态密度因为O分别位于Ba平面和Sr平面而具有BaTiO3和SrTiO3中O 2s轨道态密度的形状和特征峰,而BST {100}-O2的态密度因为O2同时与Ba和Sr成键而表现出BaTiO3和SrTiO3中O态密度的综合平均效果,与BST{110}以及BST{111}中O的态密度近似.另外,BST{100}-O3拥有三个高度基本一致的2 p态密度峰,这使它与Ti 3d轨道的杂化强于其他位置和结构中的O,即二者之间有更强的相互作用,这也和前面关于结构和键长的分析结果一致.
3.3.电荷密度
为了更加直观了解Ba0.5Sr0.5TiO3各有序构型Ti-O八面体中O原子和Ti原子之间的相互作用和成键情况,做出如图4所示的差分电荷密度图.对比图4(a)和(b),在BST{100}构型的(010)面上可以看到Ti周围的电荷因为和O3的强烈作用而偏向O3,而在(100)面上,Ti和周围的O2作用对称,电荷分布基本上也保持对称,可见BST{100}构型中Ti-O八面体的畸变的确导致[100]方向出现电偶极矩,进而使自发极化产生,和前述分析结果一致.BST{110}和BST{111}构型中不同两个平面上Ti的电荷分布也保持了很好的对称性,如图4(c)和(d),正负电荷中心重合,无自发极化,进一步印证了前面的分析.由此可见Ti-O八面体中Ti和O之间的相互作用,尤其是O 2p和Ti 3d轨道的杂化对Ba0.5Sr0.5TiO3中铁电性的产生起着关键作用,这一点与文献[6]和[7]报道相符合.

图4 Ba0.5Sr0.5TiO3各个构型的差分电荷密度图(a)BST{100}构型(010)面;(b)BST{100}构型(100)面;(c)BST {110}构型(110)面和(001)面;(d)BST{111}构型(100)面和(001)面
4.结论
使用第一性原理赝势平面波方法,得到了Ba0.5Sr0.5TiO3三种有序构型各自的稳定晶格结构,并在此基础上计算了各有序构型的Mulliken键布居、各原子分态密度和差分电荷密度图.BST{100}构型中,Ti原子沿[100]方向靠近Sr平面,偏心位移为0.040,O2原子沿[100]方向偏离Ba-Sr面心向Sr平面移动0.065,Ti-O八面体发生畸变,导致方向反平行的自发极化出现,构型处于四方相反铁电态.BST{110}构型中的O2原子也存在0.029的偏心移动,但由于Ti原子无偏心位移,Ti-O八面体仍比较对称,无自发极化,构型处于四方相顺电态.BST{111}构型以高度的对称性以及无Ti和O原子的偏心位移而处于立方相顺电态.对比各构型的能量发现,BST{100}构型更有可能出现在Ba0.5Sr0.5TiO3中.另外,Ti-O八面体中以O 2 p和Ti 3 d轨道杂化为主的Ti和O之间的相互作用,对Ba0.5Sr0.5TiO3中铁电性的产生有着重要贡献.由此可见,在Ba0.5Sr0.5TiO3中A位的局部有序性对无序结构BST固溶体的结构相变是一个重要的影响因素,可以导致从反铁电态到顺电态的转变.这一计算结果也可以对有序结构的BST铁电材料(例如层状BaTiO3/ SrTiO3钙钛矿超晶格)以及其他ABO3型钙钛矿铁电体的研究提供一定的理论参考.
[1]Sengupta L C,Ngo E,Stowell S,Lancto R,Drach W C,Koscica T E,Babbitt R W 1994 Ferroelectrics 153 359
[2]Wang X H,Lu W Z,Liu J,Zhou Y L,Zhou D X 2006 J.Eur.Ceram.Soc.26 1981
[3]Ioachim A,Toacsan M I,Banciu M G,Nedelcu L,Vasiliu F,Alexandru H V,Berbecaru C,Stoica G 2007 Prog.Solid State Chem.35 513
[4]Chou X J,Zhai J W,Yao X 2007 Appl.Phys.Lett.91 122908
[5]Nenasheva E A,Kartenko N F,Gaidamaka I M,Trubitsyna O N,Redozubov S S,Dedyk A I,Kanareykin A D 2010 J.Eur.Ceram.Soc.30 395
[6]Cohen R E 1992 Nature 358 136
[7]Cohen R E,Krakauer H 1992 Ferroelectrics 136 65
(3)创新一些学生喜闻乐见的工作方法或活动,将微信公众号等引入工作。发掘有特长老同志,将有摄影特长的老党务工作者邀请前来做宣讲,引导学生关注其微信公众号,计划邀请老职工做好爱美爱笑(校)的报告,感染带动一片,弘扬校园美、祖国美,让学生具有一双发现美的眼睛,配合书香校园。
[8]Padilla J,Vanderbilt D 1997 Phys.Rev.B 56 1625
[9]Heifets E,Eglitis R I,Kotomin E A,Maier J,Borstel G 2001 Phys.Rev.B 64 235417
[10]Sepliarsky M,Asthagiri A,Phillpot S R,Stachiotti M G,Migoni R L 2005 Curr.Opin.Solid State Mater.Sci.9 107
[11]Xue W D,Chen Z Y,Yang C,Li Y R 2005 Acta Phys.Sin.54 857(in Chinese)[薛卫东、陈召勇、杨春、李言荣2005物理学报54 857]
[12]Liu B N,Ma Y,Zhou Y C 2010 Acta Phys.Sin.59 3377(in Chinese)[刘柏年、马颖、周益春2010物理学报59 3377]
[13]Zhang C,Wang C L,Li J C,Yang K,Zhang Y F,Wu Q Z 2008 Chin.Phys.B 17 274
[14]Zhang Z Y,Yun J N,Zhang F C 2007 Chin.Phys.16 2791
[15]Yun J N,Zhang Z Y,Yan J F,Deng Z H 2010 Chin.Phys.B 19 017101
[17]Choudhury N,Wu Z G,Walter E J,Cohen R E 2005 Phys.Rev.B 71 125134
[18]Xue W D,Li Y R,Yang C 2005 Chin.J Chem.Phys.18 179 (in Chinese)[薛卫东、李言荣、杨春2005化学物理学报18 179]
[19]Wang Y X 2005 Solid State Commun.135 290
[20]Kong X L,Hou Q Y,Su X Y,Qi Y H,Zhi X F 2009 Acta Phys.Sin.58 4128(in Chinese)[孔祥兰、侯芹英、苏希玉、齐延华、支晓芬2009物理学报58 4128]
[21]Segall M D,Lindan P J D,Probert M J,Pickard C J,Hasnip P J,Clark S J,Payne M C 2002 J.Phys.:Condens.Matter 14 2717
[22]Vanderbilt D 1990 Phys.Rev.B 41 7892
[23]Perdew J P,Yue W 1986 Phys.Rev.B 33 8800
[24]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865
[25]Monkhorst H J,Pack J D 1976 Phys.Rev.B 13 5188
[26]Kuo S Y,Liao W Y,Hsieh W F 2001 Phys.Rev.B 64 224103
[27]Terai K,Lippmaa M,Ahmet P,Chikyow T,Fujii T,Koinuma H,Kawasaki M 2002 Appl.Phys.Lett.80 4437
[28]Evarestov R A,Tupitsyn I I,Bandura A V,Alexandrov V E 2006 Int.J.Quantum Chem.106 2191
PACS:71.15.Mb,71.15.-m,77.80.-e,77.22.Ej
First-principles study of ordered structures in Ba Sr TiO*
0.50.53
He Jian-Ping LüWen-ZhongWang Xiao-Hong
(Department of Electronic Science and Technology,Huazhong University of Science and Technology,Key Laboratory of Functional Materials for Electronic Information(B)(Huazhong University of Science and Technology),Ministry of Education,Wuhan 430074,China)
(Received 17 November 2010;revised manuscript received 11 December 2010)
The lattice structures and the electronic structures of different ordered structures in Ba0.5Sr0.5TiO3are calculated by the first-principles method.The results of geometry structures and overlap populations reveal that the BST{100}ordered structure is tetragonal.The O atoms in Ti-O octahedron parallel to Ba plane and Sr plane are shifted ward Sr plane by 0.065.And the Ti atom in Ti-O octahedron has a off-center displacement of 0.040.The off-center displacements of O atoms and Ti atoms result in the distortion of Ti-O octahedron,and the occurrence of antiparallel spontaneous polarization.Therefore the BST{100}ordered structure is in antiferroelectric phase.The O atoms in BST{110}ordered structure also have a off-center displacement of 0.029,while the Ti atom in Ti-O octahedron is still in-center.This tetragonal structure is in paraelectric phase.The BST{111}ordered structure is in cubic paraelectric phase.The calculated density of states shows that the hybridization between Ti 3d and O 2 p plays a primary role in the generation of ferroelectricity.The results of the present work imply that the local order of A site can significantly influences the structural phase transition of disordered BST solid solution.
barium strontium titanate,first-principles,ordered structures,ferroelectricity
*国防基础科研重大项目(批准号:A1420080168)资助的课题.
.E-mail:lwz@mail.hust.edu.cn
*Project supported by the Major Program for the Fundamental Research of the National Defense of China(Grant No.A1420080168).
Corresponding author.E-mail:lwz@mail.hust.edu.cn
