上海农业发展的实证检验1978～2009

2011-11-01徐群韩雯程毅

统计与决策 2011年7期

关键词：阶数格兰杰种植业

徐群，韩雯，程毅

（1.南京农业大学人文社会科学学院，南京210095；2.上海市徐汇区业余大学，上海200032；3.华东理工大学社会学系，上海200237）

上海农业发展的实证检验1978～2009

徐群1，韩雯2，程毅3

（1.南京农业大学人文社会科学学院，南京210095；2.上海市徐汇区业余大学，上海200032；3.华东理工大学社会学系，上海200237）

文章研究考察了改革开放以来，上海城市化进程中的农业发展状况，以向量自回归模型（VAR模型）为基础，利用格兰杰因果检验、向量误差修正模型（VEC模型）、协整回归方程（ECM模型）对上海农林牧渔四个农业部门之间的关系进行动态效应分析。研究结果显示：上海城市功能的转变致使农业产业结构调整和农业生产布局等发生了变化。改革开放至今，四个农业部门中只有种植业部门和渔业部门存在长期的协整关系以及互为格兰杰因果关系。此外，基于已构建的两个部门产出回归关系的向量误差修正模型（VEC）和误差修正模型（ECM），均可有效地根据不同预测需求进行未来产值的经济性预测。并提出了政策建议。

上海市；农业经济发展；动态效应分析；政策建议

0 引言

农业发展史，也是一部农业功能的演进史。库兹涅茨(1961)指出，农业的功能，从最初的农产品贡献，逐渐发展到市场贡献、要素贡献和外汇贡献，而在经济发展和城市化进程日新月异的今天，农业在劳动力就业、生态环境保护、观光休闲、文化传承等方面功能不断显现与增强。而刘伟明（2006）根据区域布局、功能分工、发展水平的不同，提出我国存在三种地域农业类型：农区农业、城郊农业和都市农业。三种地域农业类型也分别体现了农业所起不同功能作用的三个农业发展阶段。

农业发展阶段的划分，不仅可以使我们较准确地认识农业发展现状，更重要的是对不同发展阶段农业部门所具备特征的了解，能使我们更清楚地认识农业在整个国民经济发展中的地位以及农业与其他产业部门之间的互动关系，从而为确立适当的经济发展战略和农业发展政策提供理论依据。本文将以上海农业发展为例，分别阐述改革开放至90年代和90年代至今两个阶段，城市化进程中的农业发展概况，并在此基础上，对上海改革开放至今的农林牧渔四个农业部门发展进行动态计量分析。

1 上海农业发展概况

1.1 改革开放至90年代的农业发展

改革开放以后，随着国民经济的快速增长和社会的全面进步，上海郊区城市化进程加快。在1979～1990年间，上海人口稳定发展，其中，从1982年开始，进入了上海人口的郊区化启动阶段。伴随着人口城市化的稳定发展，农业生产主要重心逐渐转为副食品保障和提高经济效益，农业生产结构明显变化。畜牧业成为农业主导产业，畜牧业内部牛奶、禽、蛋等生产规模快速增长，种植业内部虽然仍以粮食为主导，但已经积极发展多种经营，城市化对经济作物和其他作物的需要使得这些农作物生产比重明显上升。淡水和海水养殖业的生产规模、生产区域均明显扩大。副食品生产范围由近郊向中远郊扩散，近郊地区已经呈现较为明显的城郊农业发展特征。

对于农业产业结构而言，种植业产值比重快速下降，畜牧业产值比重大幅上升并于90年代初超过种植业，渔业也获得较快的发展，但增长幅度明显低于畜牧业。1992年上海农业总产值构成中，种植业、畜牧业、渔业和林业分别占到40.2%、47.1%、11.8%和0.4%。种植业生产结构中，粮食仍是最大宗的农作物，棉花播种面积比重降至3%以下，油菜籽播种面积比重升至15.7%，蔬菜播种面积比重上升到1l.7%。畜牧业内部，禽、蛋、奶等生产快速发展，生猪饲养量则呈波动式下降。

1.2 90年代至今的农业发展

20世纪90年代中后期以来，虽然城市化的上升速率有所下降，但人口郊区化的进程在逐渐推进。上海工业化后期产业结构运行特征是在第一、第二产业协调发展的同时，第三产业开始由平稳增长转入持续的高速增长，最终成为国民经济的主导产业。在这段时期，是以城郊农业为主导，都市农业起步的发展阶段；进入21世纪，上海市农业正在开始由城郊农业向都市农业转化，初步形成与上海国际化大都市相适应的都市型现代农业基本框架。因此，为了服务于第三产业的发展，农业功能以生产和经济功能为主，同时生态、服务、社会文化等多方面的功能已经起步。

上海农业产业结构再次发生了明显变化，表现为畜牧业产值比重大幅下降，种植业产值比重稳中有增，再次成为上海郊区农业产业结构中的主体产业，并且渔业产值比重也持续上升，畜牧业和渔业产值比重相当，林业出现较为明显的增长。2009年上海农业总产值构成中，种植业、畜牧业、渔业和林业分别占到52.1%、22.82%、18.91%和3.175%。种植业结构呈现鲜明变化，粮食作物播种面积比重减少到50%以下，油菜籽播种面积下降，蔬菜播种面积比重增加到30%以上。这段时期主要农产品为：蔬菜、水果、西甜瓜、花卉苗木等园艺产品快速增长并成为主导产品，畜禽产品、粮食、油菜等大幅缩减，水产品产量明显增加。

2 农业四个部门之间的动态关系研究

上海农业产业结构发展概况的研究，需要进一步得到农业各部门之间的动态变化规律。即根据时间序列数据，利用动态计量分析方法对种植业、林业、畜牧业和渔业四个部门之间相互作用关系的具体效应进行研究。

2.1 数据来源

考虑到本文研究的是改革开放以来上海产业结构的发展状况，因此，在数据选取时，主要以1978～2009年的种植业、林业、畜牧业和渔业的农业产值指数来代表四个产业部门的发展，分别用ZY、LY、XY和YY表示，以1978年的产值指数为100。数据来源于《上海统计年鉴》（2010）。软件方面，本文采用了Eviews6.0软件对数据进行处理分析。

首先，为了避免数据的剧烈波动可能带来的异方差性，对各序列进行对数化处理，取对数之后的新序列分别用DZY、DLY、DMY、DYY表示，发展趋势如图1所示。

2.2 模型设定

向量自回归（vector auto-regression，VAR）模型通常用于多变量时间序列系统的预测和描述随机扰动对变量系统的动态影响。最一般的VAR（p）模型如下面的式子：

式中，yt是m维内生变量向量；xt是d维外生变量向量；A1…Ap和B1…Br是待估计的参数矩阵，内生变量和外生变量分别有p和r阶滞后期；εt是随机扰动项，同期之间可以相关，但不能自相关。

下文将以VAR模型为基础，利用格兰杰因果检验、最大滞后阶数、平稳性检验、VEC模型、ECM模型对四个部门之间的动态效应进行分析。

2.3 格兰杰因果关系检验

一般地，在VAR模型中应该考虑问题的另一方面，即序列y是否是x的格兰杰成因，只有在x与y互为因果时，采用VAR模型才是有效的。而格兰杰（Granger）因果检验正是一种用于考察序列x是否是序列y产生原因的方法。

对于单变量的格兰杰因果检验，EViews计算如下双变量回归：

式中，k是最大滞后阶数，通常可以取稍大一些。检验的原假设是序列x（y）不是序列y（x）的格兰杰成因。而对于该样本中的多变量情形，Eviews将进行成对的格兰杰因果检验（pair-wise Granger causality tests），检验结果如表1所示。

表1 格兰杰因果检验结果

从表1中发现，除了种植业部门与渔业部门的产出是相互影响、相互制约的，即存在互为因果关系之外，剩下的部门两两组合均不存在互为格兰杰因果关系。因此，可进一步对种植业和渔业两个部门建立向量自回归模型，两者产值指数取对数之后的图形如图2所示。

从图2中易发现种植业和渔业两个部门产出变化具有大体一致的共同趋势，并且在90年代以前，两个部门的产出虽然出现波动性上升，但增长幅度并不是很大，而进入90年代中后期以后，均呈现出较快的增长趋势。事实发展中也应证了上述结论。在上海郊区城市化和工业化发展进程中，农村耕地逐年减少，但在此情况下，上海农业产出规模与水平总体上仍保持稳定持续的增长态势。为顺应生产和市场环境的变动，发挥本地农业资源优势，满足市场需求，近几年上海农业产业结构得到不断调整，种植业和渔业生产总量规模逐年递增，畜牧业却缩减。

2.4 确定最大滞后阶数

滞后阶数的确定与格兰杰因果检验是密切相关的。在VAR模型中，Eviews提供了最为常用的LR检验统计量，最终预测误差（FPE），AIC信息准则、SC信息准则和HQ信息准则的结果，

（1）LR检验统计量

似然比（likehood ratio，LR）检验涉及两类模型，无约束模型或无限制模型与有约束模型或有限制模型。似然比统计量是指无约束模型和约束模型的最大似然值之差的2倍，即

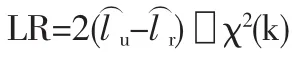
如果无约束模型和约束模型残差的最大似然之差越大，就愈加证明约束模型不充分。

（2）最终预测误差FPE

最终预测误差FPE（final prediction error criterion）是把最小值的p作为VAR模型的最佳阶数：

最终预测误差准则的优点在于它平衡了选择低滞后阶数造成偏离性的风险和选择高滞后阶数造成方差增大的风险。

（3）信息准则

模型中内生变量有p阶滞后，称其为一个VAR（p）模型。在实际应用中，通常希望滞后期p和r足够大，从而完整地反映所构造模型的动态特征。但同时，滞后期越长，模型中待估计的参数就越多，自由度就越少。因此，应在滞后期与自由度之间寻求一种均衡，一般根据AIC（Akaike info criterion），SC（Scharz criterion）和HQ（Hannan-Quinn criterion）信息量取值最小的准则确定模型的阶数，计算公式见下面三个公式。

AIC=-2l/n+2k/n

SC=-2l/n+klogn/n

HQ=-2l/n+2klog(log(n))/n

式中，K=m（rd+pm）是估计参数个数；n是观测值数目，且

在本例中，显示的滞后阶数判断结果如表2所示。

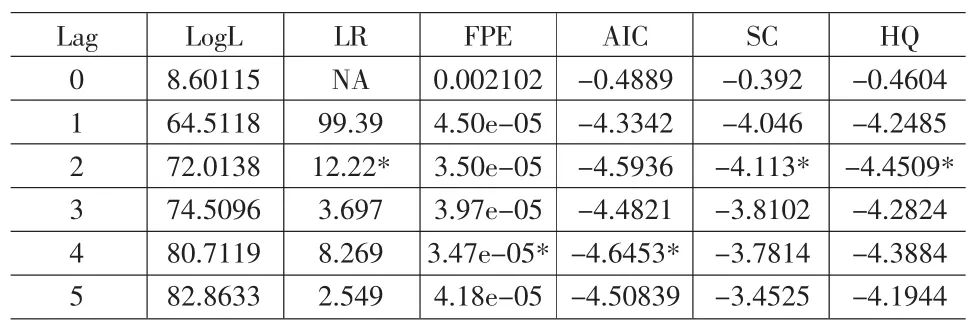
表2 滞后阶数判断结果

在表2中给出了0～5阶VAR模型的LR，FPE，AIC，SC和HQ值，并以“*”标记出依据相应准则选择出来的滞后阶数。可以看到，有超过一半的准则选出来的滞后阶数为2阶，因此，将VAR模型的滞后阶数定义为2。

2.5 平稳性检验

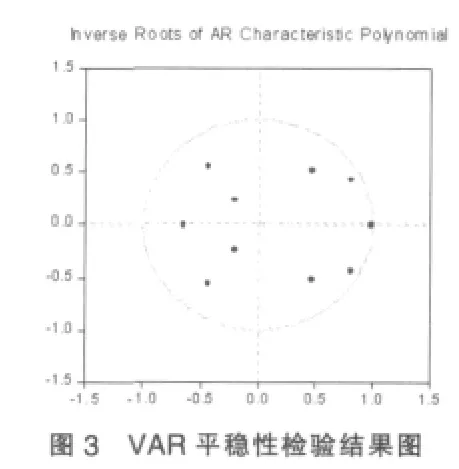
VAR模型是要求序列是平稳的，因此要检验序列的平稳性。平稳性检验可以对每一个序列分别进行单位根检验。该样例的VAR平稳性检验结果如图3所示。

由图3可知，无特征根在单位圆外，即表明序列是非平稳的。由于不满足条件，接下来则要检测是否具有长期协整关系，如果有则采用向量误差修正模型（VEC）。

2.6 VEC模型构建

（1）单位根检验

事实上，向量误差修正（vector error correction，VEC）模型是包含协整约束条件的VAR模型，应用于具有协整关系的非平稳时间序列建模。

首先，对两个序列做单位根检验，单位根检验是检验时序平稳性的一种方法，而最大滞后期可根据上述已经选择出的滞后阶数2，采用PP检验。

Phillips和Person于1988年提出了PP检验，PP检验的检验方程如下面的式子所示。

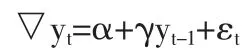
本例中选择包含常数和线性趋势项的检验方程，对DYY和DZY进行level检验，结果发现是非平稳的；而一阶差分序列均为平稳序列，即在一阶差分之后，收尾概率均小于0.1，则两个序列是同阶平稳，所以满足进行协整检验的条件。

（2）Johansen协整检验。

采用Johansen（1995）提出的关于系数矩阵的协整似然比（LR）检验方法。协整似然比检验法主要包括迹检验法和最大特征值检验法。

通过Johansen协整检验可知，迹检验法在0.05显著性水平下没有一个协整关系，而最大特征根表明在0.05显著性水平下有一个协整关系，故可以认为有且仅有一个协整关系。

（3）向量误差修正（VEC）模型

向量误差是对诸变量施加了协整约束条件的向量自回归模型。VEC模型只能用于协整关系的序列建模，将本例估计结果写成矩阵形式，得到：

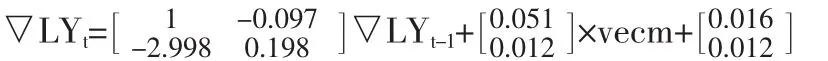
上述VEC模型是可用作以下情形：知道当期两个变量的值，求解下一期两个变量的数值，但在多数情况下，会遇到仅知道一个变量的当期值却不知另一期属性值的情形，因此，接下来将对存在协整关系的两个变量构建协整回归方程。

2.7 协整回归方程

为检验两变量xt和yt是否协整，Engle和Granger于1987年提出了两步检验法，称为EG检验。对同是d阶单整的序列xt和yt，用一个变量对另一变量回归，即

由2.6可知种植业与渔业部门可能存在协整关系，现利用EG两步法对其进行检验。

首先，分别对序列DZY和DYY进行单整检验，这里采用ADF检验法，均采用不含常数和趋势项，滞后项为0，将各序列的ADF检验统计量与相应的临界值比较，容易得出，原序列DLY和DYY都是非平稳序列，而一阶差分序列均平稳，由此判定DLY和DYY为一阶单整序列，满足协整检验前提。

其次，对变量DZY和DYY进行最小二乘回归，得到结果如表3所示。

表3 最小二乘回归结果

回归方程估计残差序列E的取值图4所示。

对序列E做单位根检验，ADF检验结果见表4所示。

表4 ADF检验结果表

其中，检验统计量为-4.1069，小于显著性水平0.01时的临界值-2.6416，可认为估计残差序列E为平稳序列，进而得到序列DLY和DYY具有协整关系。

由于已经证明序列DZY和DYY之间存在协整关系，故可建立误差修正模型。误差修正模型（ECM）的基本形式是由Davidson，Hendry，Srba和Yeo于1978年提出的，称为DHSY模型，模型为：

式中，ecm是误差修正项

在该样本中，以DYY为因变量，DZY为自变量，进行最小二乘回归，得到回归系数为2.699554，则利用GENR定义：

ECM=DYY（-1）-2.699554*DZY（-1）

也可利用差分表达式，得到的模型表达式为：

DYYt=-0.568868+0.915101DYYt-1-0.085763DZYt+0.315509DZYt-1+vt

两种方法建立的误差修正模型是等价的，模型拟合度很高，效果很好，但是第二个式子在实际预测时更常使用，虽然两个变量互为因果关系，但是此时，不可再利用DZY做因变量进行再次预测，否则会使得两个式子产生冲突。

3 结论及政策建议

基于上海改革开放至今的农业发展概况，结合时间序列数据的动态计量分析结果，本文给出了如下的结论及政策建议：

首先，上海城市功能的转变致使农业产业结构调整和农业生产布局等发生了变化。上海郊区农业产业结构优化的总体思路是保持种植业的主导地位，小幅度调减畜牧业，合理发展水产业，适度发展林业，形成种植业、林业、畜牧业和渔业协调发展，互为补充，物质和能量合理流动的循环型农业系统。

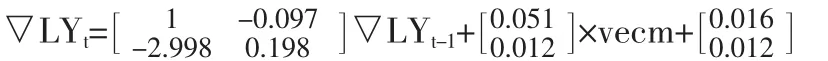
其次，关于种植业和渔业两个部门产值指数的向量误差修正模型（VEC）和误差修正模型（ECM）表达形式，两种模型均可有效地根据不同需求进行未来产值的经济性预测。其中，VEC模型的矩阵表达形式如下所示：该模型是当知道两部门当期（以年计）产值指数，预测下一期两个部门的产值指数，例如当知道2011年种植业部门和渔业部门的产值总数，要预测2012年两个部门的产值指数，可用VEC模型求得；而ECM模型表达式为：DYYt=-0.568868+0.915101DYYt-1-0.085763DZYt+0.315509DZYt-1+vt，该模型是当知道当期两个部门以及下一期种植业部门的产值指数，预测下一期种植业部门的产值指数，例如当知道2011年的种植业部门、渔业部门，以及2012年种植业部门的产值指数，需要预测2012年渔业部门的产值指数，可用上述的ECM模型求得。两种模型根据不同的预测需求都有不同的预测用途。通过对上海的四个农业部门进行动态计量分析可知，从1978年至今，只有种植业部门和渔业部门存在长期的协整关系以及互为格兰杰因果关系。因此，在以后农业政策调整中，可以抓住两个部门的特点，适当促进两个部门之间的协调发展。

总的来说，由于城市化进程的不断推进，以及上海郊区农业生产的最基本要素土地资源稀缺，上海郊区农业不可能生产满足城市全部需求的农副食品，而且在大市场大流通的环境中，从比较效益的角度考虑也没必要进行小而全的农业生产，必须有所侧重。根据上海的自然和经济技术资源条件，农业发展应以现代化、科技型农业为主导方向，促进农业增产、增收和增效，将产业结构调整的重点放在各产业内部的结构优化，品种改良和品质提升上，致力于各产业的内涵式增长，尤其要关注对种植业和渔业部门的协调式发展。

[1]贾彩彦.近代上海城市化及对城市土地利用与管理思想的影响[J].上海经济研究,2004，（4）.

[2]Henderson J V.The Effects of Urban Concentration on Economic Growth[C].NBER Working Paper,2000.

[3]Stephen J.Vogel.Structural Changes in Agriculture:Production Linkages and Agricultural Demand-Led Industrialization[C].Oxford Economic Papers,New Series，1994，46（1）.

[4]Won W.Koo,Marvin Duncan.Can Developing Countries Afford the New Food System.A Case Study of the Chinese Agricultural Sector[J].American Journal of Agricultural Economics，1997,(2).

[5]范德官,上海郊区农业现代化研究[J].中国农村经济,2000，(6).

[6]冯晓华,上海都市农业探析[J].上海综合经济,2002，(1).

[7]俞菊生,中国都市农业—国际大都市上海的实证研究[J].中国农业科学技术出版社，2002.

[8]上海实现城郊型农业向都市型农业转变研究[J].上海社会科学院学术季刊,2001，(2).

[9]刘伟明,城市化工业化进程中城市农业发展类型与对策探讨[J].中国农学通报,2005，(7).

[10]刘伟明.城市化进程中城市农业发展探讨[J].中国农业科技导报，2006，（2）.

[11]农业部软科学委员会课题组.《中国农业发展新阶段》[M].北京：中国农业出版社，2000，（8）.

[12]戴鞍钢.近代上海与周围农村[J].史学月刊，1994，(2).

[13]段洪.城市化进程中都市农业发展思考[J].产业与科技论坛，2008，(12).

[14]胡锡凤.都市农业在城市化进程中的战略定位[J].商品储运与养护，2007，（5）.

F207

1002-6487（2011）07-0118-04