基于色差法的高维数据展示方法初探

2011-11-01吴翌琳林寅陈昊

统计与决策 2011年7期

关键词：色板高维色差

吴翌琳，林寅，陈昊

（中国人民大学统计学院，北京100872）

基于色差法的高维数据展示方法初探

吴翌琳，林寅，陈昊

（中国人民大学统计学院，北京100872）

随着计算机技术的普及，我们面向的数据越来越趋于高维化，而从理论上说直观描述高维数据是一件比较困难的事情。文章通过对几种高维数据展示方法的总结和创新，成功构造了一种全新的描述高维数据的方法即色差法(MCD)。

高维数据；色差；色阶；RGB

0 引言

随着计算机技术的高速发展及其在统计应用领域的普及，目前统计学者面对的数据，无论是经济领域、商业管理领域、工程领域，还是教育心理领域等，都是高维度的数据矩阵。对这些数据的分析，入手点落在对高维度数据的一个直观描述上面。

多维数据比二维和三维数据在展示上存在着诸多困难。传统的笛卡尔坐标系在展示二维三维数据上存在着优势，但是在三维以上就无能为力。然而目前几乎所有科学、工程和商业领域的数据都是高维的，即数据集通常都包含多于三维的变量。高维数据的产生，迫切需要开发处理这些数据的工具和方法。可视化是高维数据分析的重要且必不可少的工具，它可以观测到数据的复杂结构和模式。许多数据处理方法实质上是基于可视化的，如散点图和直方图，但多数可视化方法只能同时表示两个变量，这些传统方法的弱点也给其他学科的研究带来了诸多的不便。

我们以一个经济学上的例子来阐述高维数据可视化的意义。我们知道一个地区的经济发展的快慢会由很多的诸如GDP、失业率等指标来反应。如果我们仅选取一个或者两个因素，尚可通过散点图、直方图等来比较经济的发展水平。但是如果选择了3个指标或者更多的指标，就很难画出高维的散点图来比较了，所以这个时候就不得不使用一些高维数据的可视化方法来帮助比较。

因此，本文旨在对已有的高维数据直接描述方法进行比较分析，同时提出利用计算机色阶和色差来展示高维数据的方法，以期为高维数据的模型研究提供前期较为直观的数据展示。

1 色差法的基本概念及操作原理

1.1 色差法基本原理

色差法的基本原理为：每个样本按照维度分段，然后在每段色带上根据样本的数值分布来体现为不同的颜色。从而，一个样本就是一个横向的色带，所有的样本组成一个色板。

色差法可以根据需要进行分段长度以及样本宽度的调整，考虑到人眼对颜色的识别效应我们建议最小的可识别色块面积应该大于10×10像素。由于形状对于色差法没有数据上的意义，所以我们建议使用色差法的研究学者可以采取放大的方法来观察局部差异，也采取缩小的方法来观察整体差异。这就是色差法优于脸谱法和安德鲁曲线方法之处。

1.2 色阶

从理论上说，色阶是颜色亮度的指数指标，从白到黑一种是256种亮度。目前表示颜色有着多种方法，像最常见的RGB示色法，HSL示色法以及CMYK四色印刷表示法等。一方面为了让色阶的变化能够保存连续性，另一方面根据理论研究表示在黑白两色的相近色方面人类肉眼的判读力比在寻常色谱图上的判读力小。此外，为了避开色阶的循环性，我们采取RGB的标示法，以紫色表示数据中的最大值，红色表示数据中的最小值，结合人们对颜色以及热度的差别，从暖色开始到冷色就是极小值到极大值的过程。

由于颜色的表示方法取决于各种不同的系统环境（包括数值范围），我们采用的是被广泛使用的RGB坐标表示方法，每一种原色的强度依照8比特的最高值分为256个值。实际上我们采用RGB方法忽略了部分的颜色。正常来讲RGB方法能够表示1670万种颜色，不过人眼只能识别其中100万种。而本文的色差法选择的颜色范围基本满足HSL方法中的色相变化规律，不过由于HSL编码在不同的设备上可能会对饱和度等的定义存在差异，类似的方法还有HSV颜色编码方法，而实际上本文采用色差法的RGB色阶就是HSL定义的纯色阶（不包含白色以及黑色以及灰色等与饱和度亮度有关的数值），这是肉眼能够清晰辨别级别的基础。所以说色差法并不仅仅是把数值映射到颜色板上，还考虑了人眼的识别效率，从而能够更好展示数据特点，达到满足高维数据展示的要求。

从RGB表示方法来看，紫色是R:255，G:0，B:255，然后从R开始递减，最后的红色是R255G0B0。根据色谱的分界点我们做出了如表1的表格。

从色阶变化来看，我们发现尽管RGB是连续的一个色阶，但是RGB的变化并不是一味增长，但是为了数据表示的方便我们还必须进行单一的连续化，所以我们定义了如表2的转化关系。

2 色差法的应用

根据研究对象和目的的不同，色差法有两种使用方式，精细使用以及粗糙使用，虽然使用的方式不同，但是其原理都是相同的。

2.1 精细使用

精细使用就是先确定某个具体维度的最大值和最小值，然后转化为0到1275的一个位置参数，总共1276个位置，最小值赋值1，最大值赋值1275，允许中间有空值。精细使用的方法中颜色对应的是数据的水平。以此类推，每一组数据都按照此法来进行转化，从数据变为对应的颜色，画成一个色带。那么N组数据就对应有N条色带，组成一个色板。该使用方法适用于数据跨度比较大的定距变量。

2.2 粗糙使用

粗糙使用则是把单维度的所有数据排序，然后再根据位置映射到0至1275之间，粗糙使用的方法中颜色对应的是数据的相对位置。其他的均与精细使用相同。这种使用方法主要关心的是数据的秩，适用于排名数据或者一些非参数模型的数据展示。

2.3 两种使用方法的差异

（1）当数据比较“稀疏”的时候，采用精细方法对于数据的水平很敏感，如果有差异能够很快看出来；当数据比较“密集”的时候，采用粗糙的方法对于数据的相对位置很敏感，如果有差异能够很快看出来。

（2）粗糙使用对于样本量比较小的数据，由于采用相对位置，能够扩大颜色的跨度，从而相对来说差异会显得更“明显”，尤其是对于相邻的数据，这时候可能会对数据的差异程度产生误判（从颜色角度看）。

（3）精细和粗糙仅仅是针对数据度量的两个尺度，即实际水平和相对水平来谈的，跟最后的结果并无直接关系。

3 色差法实证分析

为了能更加清楚地阐述色差法的作用，我们使用的数据是一个随机模拟的6维数据，样本数为12。数据表1。我们用脸谱法、平行坐标轴法、安德鲁斯曲线法、色差法这四种方法分别描述此高维数据如表3。

表1 数据分位点与颜色表示

表2 数值与颜色转化表

表3 模拟生成的数据

3.1 脸谱图、平行坐标轴法、安德鲁斯曲线法展示

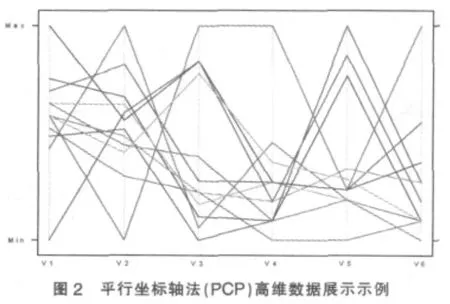
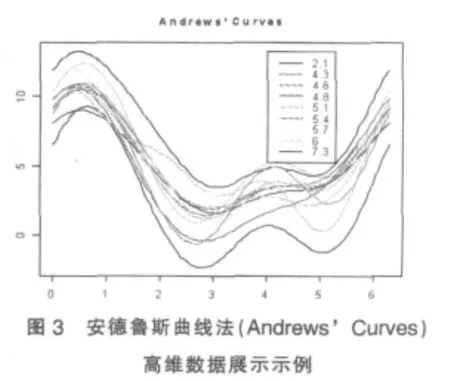
脸谱图、平行坐标轴法、安德鲁斯曲线法分别见图1、2、3。对比这三种方法，我们不难发现每一种方法都各有其优点，比如脸谱图发容易发现异常样本点，平行坐标法直观展示同一样本在不同维度上的变化，安德鲁斯曲线法利用巧妙的降维体现样本之间的近似程度。总体而言，虽然以上每一种的方法都能有效的描述出高维数据，但是通过图形是难以对于数据的分布有个大体的判断。而我们所提出的色差法则可以通过颜色的不同，对于总体数据的分布有个初步的认识。

3.2 色差法（MCD）

3.2.1 相对水平

首先对数据使用色差法进行相对水平的展示。根据每个维度数据特征，按照自身维度内部的大小，进行0～1标准化，这样表示出来的分布特征是每个维度内部的特征。其图像特点是每一列都会有最小值（红色）和最大值（紫色）。这样，单列抽出来分析的时候，能够看清楚每个维度分布。相对水平的主要缺点就是不同列之间不能够直接的比较。

为了以防读者遗忘，我们把色带的颜色所包含的意义再次阐述一下。依照下图：随着颜色由红色向紫色过渡，数据从大到小过渡，红色代表最小的数，紫色代表最大的数。则相对水平色板如图4。

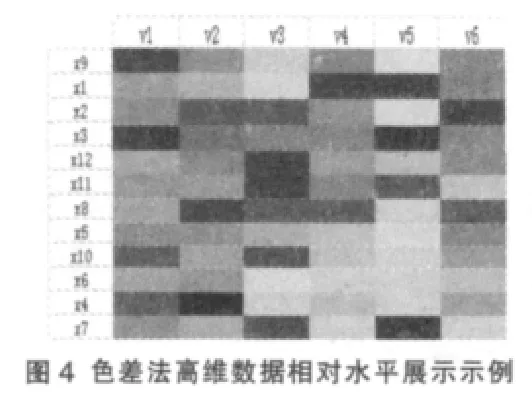
相对水平色板展示的是样本在不同维度下的相对位置，为样本整体水平的相对位置和均衡度给出相应的判断，比如这个色板展示的结果看来，样本1在第4、5、6个维度上显示出较弱水平，而前面第1、2、3维度也没有表示较高位置的冷色系出现，因此可以断定样本1在这12个样本的比较中相对水平较低。而再看看样本3，其六个维度的数据分布在两端，可见该样本的均衡度较差，数据较为极端化。总体而言，相对水平色板类似于平行坐标法，但比之更为直观易懂。

从应用角度看来，相对水平的色板适用于展示经济方面竞争力评价或者指标体系评价的高维数据，以颜色渐变直观看出比较对象间的竞争关系，水平差异以及发展结构，为进一步指标选取和模型构建打下基础。

3.2.2 绝对水平

另一种常用的色板是绝对水平的色板，其构建方法如下：首先按照每个维度计算出标准差，然后数据除以标准差以便去除量纲，不需要进行中心化。从而所有的数据现在呈现于同一个“度量范围”。然后进行0～1化后再映射到0～1276。其图像特点是整个色板只有一个最小值（红色）和最大值（紫色），其应用特点是全部数据可比，可以看出每一列的最值与其他值的区别（看出偏离程度），此外还可以看出不同的列之间数据水平的差异。绝对水平的缺点主要是削弱了每一列内部的分布色彩差异，数据量扩大导致了相邻的数据色阶差异程度缩小。绝对水平色板如图5。

我们可以看出来，这12样本6维度的数据中，最大值为第2行第2列的数，最小值为第2行第6列的数，整个色板浅蓝和绿色为主，说明中间的数据较多，数据分布相对均衡。绝对水平色板适用于进行维度方向的比较，比如从第一维度和第二维度的比较看来，第二维度的水平要显著的高于第一维度，如果维度表示的是时间序列，则通过色板可以看出第二年比第一年有显著的增长。

从应用角度看来，绝对水平色板适应于对样本在不同维度上的变化趋势做分析，因此，尤其适用于时间序列数据，每个维度即为一个时间点，从上图可以显著看出，假设这批数据为时间序列数据的话，第2期是一个峰值，第4和第6期分别为两个低谷，可以看出样本数据的波动性。同时，该色板也适用于分析同一口径的高维数据，比如说心里研究的量表或者问卷调查的分类数据等，看出不同指标间的水平差异。

4 色差法的缺陷

虽然色差法克服了多个维度之间的展示问题，但是本身却有着一个严峻的缺陷，那就是因素水平。每一个维度，色差法最多能够提供的水平位置数目是1275，再多的水平已经超过了人眼的识别范围。而且，如果考虑人眼的识别效率，当一组数据的个数大于500个的时候，人眼可能很难分辨出颜色的细微差异。这一点可能是制约色差法推广使用的最大弱点。因为我们知道，多元统计分析常常要与超高维数据，超大量数据打交道，仅仅500个可识别水平可能很难满足研究学者的需要。

不过，由于现在精密仪器的推广与使用，我们可以借助仪器的判断来辨别出实际颜色的差异，因而在实际的使用中，我们可以处理的水平数是可以达到色差法理论允许的最大值的，即1275个水平。这个承受水平对于一般的研究来说应该是可以满足的。