基于Monte Carlo随机模拟的几种正态性检验方法的比较
2011-11-01章刚勇阮陆宁
章刚勇,阮陆宁
(南昌大学经济与管理学院,南昌330031)
基于Monte Carlo随机模拟的几种正态性检验方法的比较
章刚勇,阮陆宁
(南昌大学经济与管理学院,南昌330031)
文章概述了几种主要的正态性检验方法,指出了它们的联系和区别。在Monte Carlo随机模拟的基础上,计算了Shapiro-W ilk检验、Kolmogrov-Sm irnov检验、Gramer-von M ises检验和Anderson-Darling检验等四种检验方法在显著性水平为0.01,0.05和0.1,样本容量为10,20,30和100的条件下的检验功效。并在比较和分析各检验方法功效的基础上,给出了相关结论和建议。
正态性检验;功效;随机模拟
0 引言
正态意味“正常性态”,指若在观察或实验中不出现重大失误,则结果应遵从正态分布。这个看法既有大量的经验事实支撑,也有理论依据(中心极限定理)。基于正态总体的一系列重要检验统计量有形式完美简洁且在计算上可行的特点。但在小样本情况下,总体服从正态分布的假定不成立时,相应的参数检验是失效的,统计推断是不可信的。对于假定是否合理,需要使用已有的观测数据进行正态性检验。判断一列数据的分布是否具有正态性规律,有许多种方法。其一:使用图示法从直观上判断,如频率分布直方图,QQ图(四分位数图)和PP图(百分位数图)等;其二:规范检验法,主要包括:卡方拟合优度检验,柯尔莫哥洛夫检验,W检验,D检验,偏度检验和峰度检验等等。各正态性检验方法有无异同,主流的检验方法有哪些,检验效果如何,在实践中应选择何种检验方法,应注意哪些问题?本文试图去回答这些问题。
1 正态性检验
正态性检验方法的原假设一般为H0:数据服从正态分布;相应的备择假设为H1:数据不服从正态分布。在这种意义下,这类检验有时也称非正态性检验(non-normality test)。规范性检验方法主要有:
1.1 W检验(Shapiro-W ilk检验)
W检验是Shapiro和Wilk在1965年提出来的。W检验的基本思想是在数据服从正态分布的原假设下,通过数据的顺序统计量对经标准化后的顺序统计量的期望值线性回归,得出拟合优度。拟合优度越大,表示两变量的相关程度越高,数据越近似服从正态分布。W统计量的值夹在0和1之间。W检验一般步骤为:
(1)把n个样本观测值按由小到大的顺序排列:x(1)≤x(2)≤…≤x(i)≤…≤x(n);
(2)W检验的统计量为:

(3)根据给定的显著性水平α和样本容量n,查统计量W的p分位数表,确定α分位数Wα的值。其分位数表通过计算机模拟产生;
(4)计算统计量W的值,若W 上述的W检验是一种有效的正态性检验方法,但由于随着样本容量的扩大,分位数Wα的确定意味着庞大的随机模拟工作量,并且由于W的高于一阶的矩是未知的,有些分布拟合技术不能采用,一般适用于样本容量为3至50的样本。针对于此,D Agostino(1971)提出了D检验,与W检验类似,其基本思想也是在总体服从正态分布的原假设下,通过构造一个统计量评价样本的顺序统计量与其期望值之间的线性关系来判断样本数据是否取自于一正态总体。它所适用的样本容量n的范围为:50≤n≤1000,这种检验不需要附系数表,其检验统计量的分布渐近正态,但收敛速度较慢,当样本容量不太大时用正态分布去近似,误差太大。 对于一般的n,W的分布的密度函数形式目前还未确定。当对于样本容量为3时,W的分布是确定的,可用于计算显著性水平;当样本容量大于3时,可通过计算机模拟的结果来计算显著性水平。随着计算机技术的发展,随机模拟工作也变得简单和轻松,Royston(1992)通过随机模拟的结果构造了一个近似正态变换Zn,扩展了W检验: 在这γ,μ,σ是样本容量n的函数,通过随机模拟取得。Zn值越大,意味着数据偏离正态分布的程度越大。这样,W检验适用范围扩展到样本容量为4至2000的样本的正态性检验。这样,D检验方法渐渐被统计软件的有关正态性检验的模块所摒弃[1]。 若总体的分布函数F(x)未知,但有样本观测值(x1,x2,…,xn),把它按由小到大的顺序排列成x(1)≤x(2)≤…x(n),得到经验分布函数: 根据格里汶科定理,当n很大时,Fn(x)是F(x)的良好近似。经验分布函数检验法原理是:先假设总体服从某一特定的分布,再根据样本数据得出其经验分布函数,通过计算经验分布函数与总体分布函数的偏差的某种形式来确定原假设是否成立。Kolmogrov和Smirnov为这类检验方法做了开创性的工作[2]。这类检验方法是通过度量经验分布函数与原假设成立时的总体分布函数之间的偏离来构建检验统计量,因此只适用于总体分布完全已知的情况,当总体理论分布包含未知参数时,人们往往用样本的信息也对参数进行估计。检验方法不但可以检验样本数据是否服从正态分布,也能检验数据是否服从其它分布。对于正态分布,假设总体服从具有参数μ和σ2的正态分布,其中μ和σ2可以由样本均值和样本方差代替。 (1)K-S检验(Kolmogrov-Smirnov检验) Kolmogrov在1933年提出了统计量Dn,并给出了统计量的极限分布。其具体形式为: Smirnov(1948)给出了用于估计经验分布拟合度表,张里千(1956)给出了Dn的有限分布形式。 (2)Gramer Von-Mises检验 Gramer Von-Mises(1928)定义了检验统计量W2,以此度量经验分布函数与总体分布函数的偏离程度: (3)Anderson-Darling检验 Anderson-Darling(1954)提出了检验统计量A2,以此来度量经验分布函数与总体分布函数的偏离程度: 当具有总体在偏度方向或峰度方向具有偏离正态的先验信息时,使用偏度检验或峰度检验是适宜的。该类检验的使用条件是已知总体在偏度或峰度的方向上具有偏离正态的特点,且偏离方向是明确的。如果在实际应用中,有关的先验信息是未知的,需要用使用其它的检验方法(梁小筠,1997)。实践中,数据来自于何种总体,往往是不可知的,故在正态性检验中难于使用偏度检验和峰度检验方法。 目前,主流的规范性正态检验方法主要是几种无方向正态性检验方法,主要包括Shapiro-Wilk检验、Kolmogrov-Smirnov检验、Gramer-von Mises检验和Anderson-Darling检验。后三种是经验分布函数检验法。哪种方法更好,需要比较它们的功效。以下将在Monte Carlo随机模拟基础上计算这四种检验方法的功效。 Monte Carlo方法是使用随机抽样技术和计算机模拟技术去近似地解决数学或物理中的问题的一种方法,特别地当大批的值都具有计算出的概率,作为问题的解时[3]。在统计定理的前提假设不成立,或当有关理论较弱或不存在的情况下,Monte Carlo方法经常被用于评价违背假设的后果和确定统计量的抽样分布。 在原假设为总体服从正态分布下,备择假设为总体服从非正态分布。非正态分布有许多,本文挑选了8种分布作为非正态分布的代表,分别为Beta分布、二项分布(bin(k,0.5))、卡方分布、泊松分布、t分布、对数正态分布、Tukey分布和Weibull分布。通过改变有关参数的值,共有32种备择分布[4]。参数是用于控制备择分布的偏度与峰度,用于考查检验方法对偏度和峰度的敏感性程度。其中Weibull分布的密度函数为: 表1 α=0.01时,四种正态性检验方法的检验功效(%) a>0,为形状参数;b>0,为位置参数。在这固定b=1。 表2 α=0.05时,四种正态性检验方法的检验功效(%) 表3 α=0.1时,四种正态性检验方法的检验功效(%) 表4 各检验功效的描述性统计 表5 α=0.01,n=10时,四种正态性检验方法功效的均值检验(H0:均值相等) 由于抽样的随机性,我们可能作出正确的决策,也可能犯两类错误:当原假设为真时,可能作拒绝的决策,称为第I类错误(拒真);当原假设为错误时,可能作接纳的决策,称为第II类错误(纳假)。当样本容量确定时,犯两类错误的概率不能同时被控制。一种较好的检验方法,应该在控制犯第一类错误的概率,即显著性水平α下,使得犯第二类错误的概率β较小,即使得检验的功效1-β较大(拒假的概率较大)。显著性水平α一般取值为0.01,0.05和0.1,选择α时,要考虑在实际问题中,当原假设为正确时,却拒绝了,所要付出的代价。 前文所述的四种检验方法有无差异,效果如何,哪种方法比较好,在实际应用中应选择何种检验方法,需要比较它们的检验功效。我们采用Monte Carlo实验进行随机模拟,计算出各检验方法的功效。主要步骤如下: (1)产生服从前面所述的32种备择分布的随机数,并确定样本容量n,在这n分别取10、20、30和100。这样共产生四批随机数32×10、32×20、32×30和32×100; (2)上一步骤一共产生128个服从某一特定的备择分布的随机数系列,对每一个系列实施四种正态性检验方法,并记录各自的p值; (3)设定样本的个数为2000,即重复第(1)步和第(2)步2000次,并收集各自的p值。在样本容量确定下,对每一个随机变量系列实施一种检验方法,产生了2000个p值; (4)把得到的p值与选定的显著性水平进行比较,分别计算出在显著性水平α=0.01、α=0.05和α=0.1下,2000个样本中,拒绝正态分态原假设的样本数,并以此样本数在总样本数2000中所占的比例,近似地表示各种检验方法在既定的样本容量,既定的备择分布和既定的显著性水平下的检验的功效。 经模拟计算的结果如表1、表2和表3所示。表中的数值表示检验的功效(%),数值是在统计软件SAS环境下通过编程计算产生,计算过程和结果可以重复验证。其中:检验方法W、KS、W2和A2分别表示Shapiro-Wilk检验、Kolmogrov-Smirnov检验、Gramer-von Mises检验和Anderson-Darling检验;表内的第1列为备择分布的形式,beta表示β-分布,bin表示二项分布,chisq表示卡方分布,P表示泊松分布,t表示t分布,LN表示对数正态分布,Tukey表示Tukey分布,Weibull表示Weibull分布,各分布后紧随的括号里的数表示各自的参数。 通过比较随机模拟的结果,可以看出四种正态性检验的功效随样本容量的增加而增大,并随显著性水平α的增大而增大。四种检验方法在小样本(n=10,n=20)条件下,其检验的功效一般较低。 注意到,当备择分布为beta(3,2)、binomial(20,0.5)、chisq(10)、Possion(10)、t(20)、Tukey(0.7)、Tukey(1.5)和Weibull(2)等分布时,各检验的功效都较小。即使在大样本(n=30,n=100)条件下,各检验的功效也不大。这些分布的特点是偏度为0或接近于0,峰度接近于3,在大样本的条件下一般有近似服从正态分布的性质。此时若各检验方法没有拒绝正态性原假设是正常的。同时,还注意到当备择分布为binomial(4,0.5)、chisq(1)、chisq(2)、Possion(1)、Tukey(10)、Tukey(20)和Weibull(0.5)时,即使在小样本(n=10)的条件下,各检验方法的功效都很大。这些分布的特点是峰度异于3,或偏度异于0。各检验方法对备择分布形式、并且对分布的非对称和厚尾的特点都较敏感。 若把备择分布当一整体,从直观上难于判断各类检验方法功效的差异。表4给出了在既定的显著性水平下和样本容量下,各检验的功效的描述性统计。比较而言,小样本时,Kolmogrov-Smirnov检验的功效均值比其他三种检验的要小,但其功效的标准差要小,相对较稳定;而在大样本时,Kolmogrov-Smirnov检验的功效的均值比其它三种检验要小,标准差却要大。Shapiro-Wilk检验、Gramer-von Mises检验和Anderson-Darling检验功效的均值和标准差,无论在大样本和小样本的条件下,差别都甚小。 我们采用方差分析、Wilconxon得分、中位数得分、Van der Waerden得分和Savage得分等方法[5]对四种正态性检验方法的功效进行检验,用以判断这些检验方法的功效有无显著性差异。根据表1、表2和表3的数据,在给定的显著性水平(3种)、给定的样本容量(4种)下,共有12种组合,需要进行12次检验。表5给出α=0.01,n=10时四种检验方法功效的均值比较,检验的原假设为四种正态性检验方法的功效的均值相等,各检验的P值显示没有理由拒绝原假设,即认为四种正态性检验方法的功效的均值无显著性差异。在其它α和n的组合下,其相应检验的p值都在0.9左右(检验结果略)。 本文概述了几种常用的正态性检验方法,并在Monte Carlo模拟的基础上,分别计算和比较了Shapiro-Wilk检验、Kolmogrov-Smirnov检验、Gramer-von Mises检验和Anderson-Darling检验等四种正态性检验的功效。主要结论和建议有: (1)在正态性判断的几种无方向性规范检验方法中,Shapiro-Wilk检验与D Agostino检验的思想类似,Shapiro-Wilk检验原只适用于检验样本容量为3至50的样本,但随着Royston(1992)的研究,其适用范围扩展到样本容量为4至2000的样本的正态性检验,D Agostino检验渐渐被统计软件相关模块所摒弃;经验分布函数检验法是通过度量根据样本数据得到的经验分布函数与原假设成立条件下的总体分布函数之间的偏离来构建检验统计量的,其中以Kolmogrov-Smirnov检验为主; (2)四种检验方法的功效随样本容量的增大而增大,随显著性水平的提高而增大;但在既定的样本和显著性水平下无显著性差异。在应用中,在已考虑了犯第I类错误所付出的现实代价的前提下,可以把显著性水平定为0.1;当实际可获得的数据较少时,使用正态性检验要小心; (3)四种检验方法对备择分布形式,备择分布的非对称性和厚尾的特点都较敏感。相对来说,小样本时,Kolmogrov-Smirnov检验的功效均值比其他三种检验的要小,其功效的标准差比其他检验方法小,相对较稳定;在大样本时,Kolmogrov-Smirnov检验的功效的均值比其它三种检验要小,标准差却大。 (4)无论在何种显著性水平下,在大样本或小样本的条件下,四种检验方法检验功效的均值无显著性不同。这并不是一个好的结论,这样的结论不能给在实践中应采用何种检验方法提供一个明确的指导。在实际应用中,较好的办法是同时使用四种检验方法对样本进行正态性检验,若有一种检验方法p值较小,并在选定的显著性水平下拒绝了原假设,可以认为所检验的数据不服从正态分布。 [1]梁小筠.正态性检验[M].北京:中国统计出版社,1997. [2]张里千.论柯尔莫哥洛夫统计量的真确分布及其渐近展开[J].数学学报,1956,(3). [3]陈希孺.数理统计引论[M].北京:科学出版社,1981. [4]孙山泽.非参数统计讲义[M].北京:北京大学出版社,2000. [5]Royston,P.Approximating the Shapiro-Wilk W-Test for Nonnormality[J].Statistics and Computing,1992,(2). [6]Smirnov,N.Table for Estimating the Goodness of Fit of Empirical Distributions[J].Annals of Math.Stat.,1948,19. [7]D Agostino.An Ominous Test of Normality for Moderate and Large Size Samples[J].Biometrica,1971,58. (责任编辑/亦民) C812 A 1002-6487(2011)07-0017-04
1.2 经验分布函数检验法




1.3 偏度检验与峰度检验
2 Monte Carlo实验设计及模拟结果
2.1 备择分布




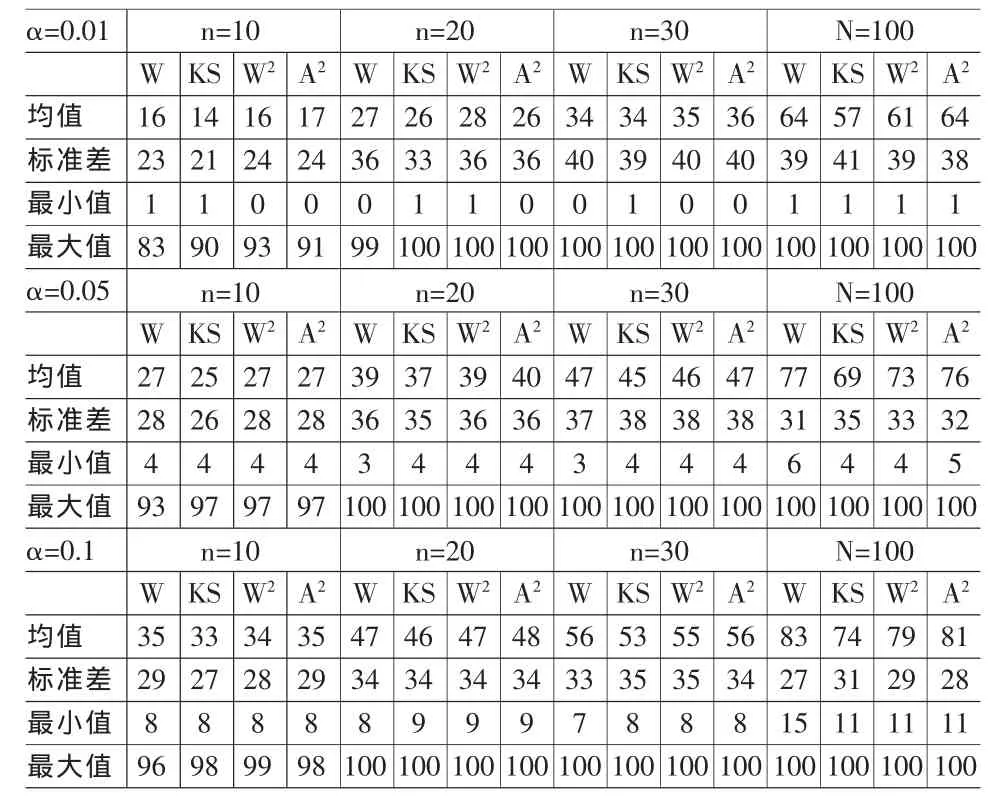

2.2 样本容量、两类错误和检验的功效
2.3 实验步骤及经模拟计算的结果
3 引检验功效的比较
4 结论与建议
