正项级数对数判别法的极限形式

包虎

（赤峰市教育教学研究中心，内蒙古赤峰024000）

正项级数对数判别法的极限形式

包虎

（赤峰市教育教学研究中心，内蒙古赤峰024000）

给出了判别正项级数敛散性的一种对数判别法的极限形式.

正项级数；敛散性；对数判别法；极限形式

文［1］给出了如下判别正项级数敛散性的对数判别法：

若n≥n0时1，则级数发散.

为了便于使用该对数判别法，判别正项级数的敛散性，下面给出它的极限形式：

证明当10，使q-ε=α>1，由数列极限的定义，N，当n>N时,有

当n>N时,

当-∞≤q<1时，任意选取适当小的ε>0，使q+ε=β<1，由数列极限的定义，N，当n>N时,有

当n>N时,

解因为

由罗比达法则知，

解因为

由罗比达法则知

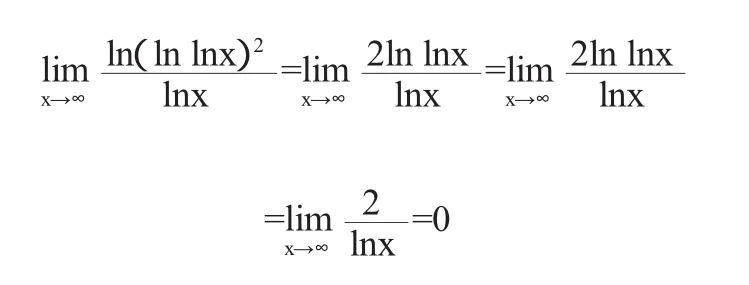
解因为

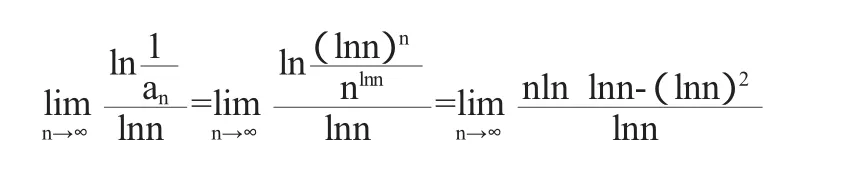
由罗比达法则知

例4判别级数的敛散性.

解因为

由上述四个例子可以看出，正项级数的对数判别法主要适用于判别幂指型级数∑u（n）v(n)的敛散性.

〔1〕费定晖，周学圣，B.∏.吉米多维奇.数学分析习题集题解（四）.济南：山东科学技术出版社，1980：24,42—13,65.

〔2〕包虎.广义积分的对数判别法.甘肃教育学院学报(自然科学版)，1999（增刊1）:4—5.

O172

A

1673-260X（2011）01-0003-02