基于熵权和可拓理论在评标中的应用

陈伟珂， 龙昭琴

(天津理工大学管理学院，天津 300384)

在工程施工市场上，招投标已经成为工程项目发包与承包所采用的一种规范化交易方式。在实际的招投标管理活动中，评标是招投标管理过程中的重要环节。但是，不规范行为不仅影响了招标人利益和投标人之间公平竞争，而且严重扰乱市场秩序。而投标人的确定又是一个非常复杂的问题，评价指标具有动态性和矛盾性，同时评标涉及到定性分析和定量分析，因此建立一种能客观评判投标人的数学方法确定投标人，一直是解决招投标管理的公平、公正、公开问题的关键[1]。

可拓理论是蔡文先生1983年将物元理论和可拓集合理论相结合提出的一种探讨处理矛盾问题的新方法。把可拓理论引入物元概念，把事物的质与量有机结合起来，以物元作为认识和分析事物的基本逻辑单元。他通过可拓集合将原来定性描述事物性质问题转化为定量化描述[2]。评标是综合评价问题，评价投标人所涉及到的指标既有定性指标，又有定量指标，而各指标间有的是互相矛盾的，有的又是互为统一的，评价时需要将互相矛盾的指标运用模型统一进行系统综合评价[3]。可拓理论能够有效解决评价中的矛盾问题、动态问题、定性与定量问题，将该方法应用到评标过程中评价投标人的优劣，解决了评价指标定量问题，增强了评价指标对评定结果贡献度，因此，选用可拓模型。

在建立了评标评价指标体系的基础上，基于可拓理论构建评标物元模型，利用可拓理论中经典域与节域对投标人评价等级进行划分。通过关联函数值的计算，得出评价指标与投标人综合得分值之间的关联程度，基于熵权对投标人综合得分进行排序优选确定投标人。应用基于熵权的可拓学理论进行评标，与其他评标方法的不同之处在于，它具有统一的评价模型，特别是把实变函数中距离的概念拓展为距的概念，使得关联函数值域范围得到了拓展，把评价指标由单一的确定值转变为区间值，从而能更全面地评价对象属于集合的程度，增强评价指标与综合评分值之间的关联程度，提高评价指标对评标结果的贡献度， 避免了主观判断投标人的弊端。

一、基于可拓学和熵理论的评价步骤

(一)物元模型的表示方法

物元模型可以用事物、特征名和对应量值组成的有序三元组来表示[4]。

(1)

式中：N为事物；ci为N的特征(i=1，2，…，n)；Ui为对应特征的量值(i=1，…，n)。

综合评标评价物元模型构建的第一步：物元事物N的选择，特征的确定(即形式审查、资格审查、响应性审查)，对应特征量值的设置(即待评价事物各指标的实际值)。该步骤使得各评价指标与指标实际值统一到综合评标评价物元模型中，使两者之间建立量化的模型数值关系，为后续系统、综合的评价计算进行奠定基础。

(二)经典域与节域

(2)

式中：N0j为所划分的j个设计等级；cj为设计等级的特征(i=1，2，…，n)；X0ji为N0j关于特征ci所规定的量值范围，即各设计等级关于对应的特征所取的数据范围——经典域(i=1,2，…，n)。

(3)

式中：RP为物元可拓模型；P为设计等级的全体；XPi为P关于ci(i=1，2，…，n)所取量值的范围，即节域。

综合评标评价物元模型构建的第二步：经典域和节域的划分。根据评标的等级标准，划分为优、中、差三个等级，可得综合评价物元模型的经典域，综合评价物元模型中评价级别的全体值域为节域。评价物元经典域和节域的划分是后续计算关联函数的根据，同时也是关联函数值的值域范围。经典域和节域的划分区间大小直接关系到评价指标对最终评标结果的贡献度。

(三)计算关联函数

利用距地定义，

(4)

计算x关于X0,X的位置值，记为

D(x，X0，X)=

(5)

各待评价指标关于评价类别j的关联函数值

(6)

综合评标评价物元模型构建的第三步：依据前两步评价指标的确定，经典域和节域的划分，计算距和关联函数值。综合评价物元模型将实变函数中距离的概念拓展为距的概念，使得关联函数值域范围得到了拓展，把评价指标由单一的确定值转变为区间值，从而能更全面地评价投标人属于集合的程度，增强评标评价指标与综合评分值之间的关联程度，提高评价指标对评标结果的贡献度。

(四)各评价指标熵权系数的确定

设有m个评价对象，n个评价指标，各评价对象的评价指标组成矩阵V，vij。在信息熵计算前，必须把数据规范化：

(7)

信息熵是系统无序程度的度量，其定义为

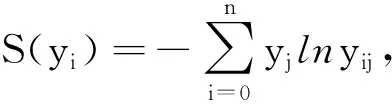
(8)

信息熵S(yj)越小，指标信息的信息量越大，该指标权重也越大；反之，该指标权重越小。因此，可以根据各项指标的变异程度，利用信息熵计算各指标的权重——熵权[5]。

首先求输入熵：

Sj=S(yj)/lnm

(9)

然后计算指标的差异度：

Gj=1-Sj,1≤j≤n

(10)

最后计算熵权：

(11)

必须满足公式：

(12)

因此，关联函数可以按公式计算：

(13)

式中：K(p)为p的关联程度。

综合评标评价物元模型构建的最后一步：根据计算所得的熵权和上步所得关联函数值，最终得出各投标人的关联度，由此确定投标人的综合得分值。如果Kj(p)=maxK(p)(j=1,2,…,n)，则优选Kj(p)。

二、实例应用

以某工程项目评标为例，说明可拓理论和熵权在招投标管理的评标环节中确定投标人的应用。

某工程项目进行招投标，共有A、B、C、D、E投标候选人。进行评标时，首先确定评价指标，使评标专家根据所设指标对投标人进行评价打分。

(一)评价指标

工程评标主要包括形式评审、资格评审和响应性评审，评标专家对投标人打分汇总表如表1。

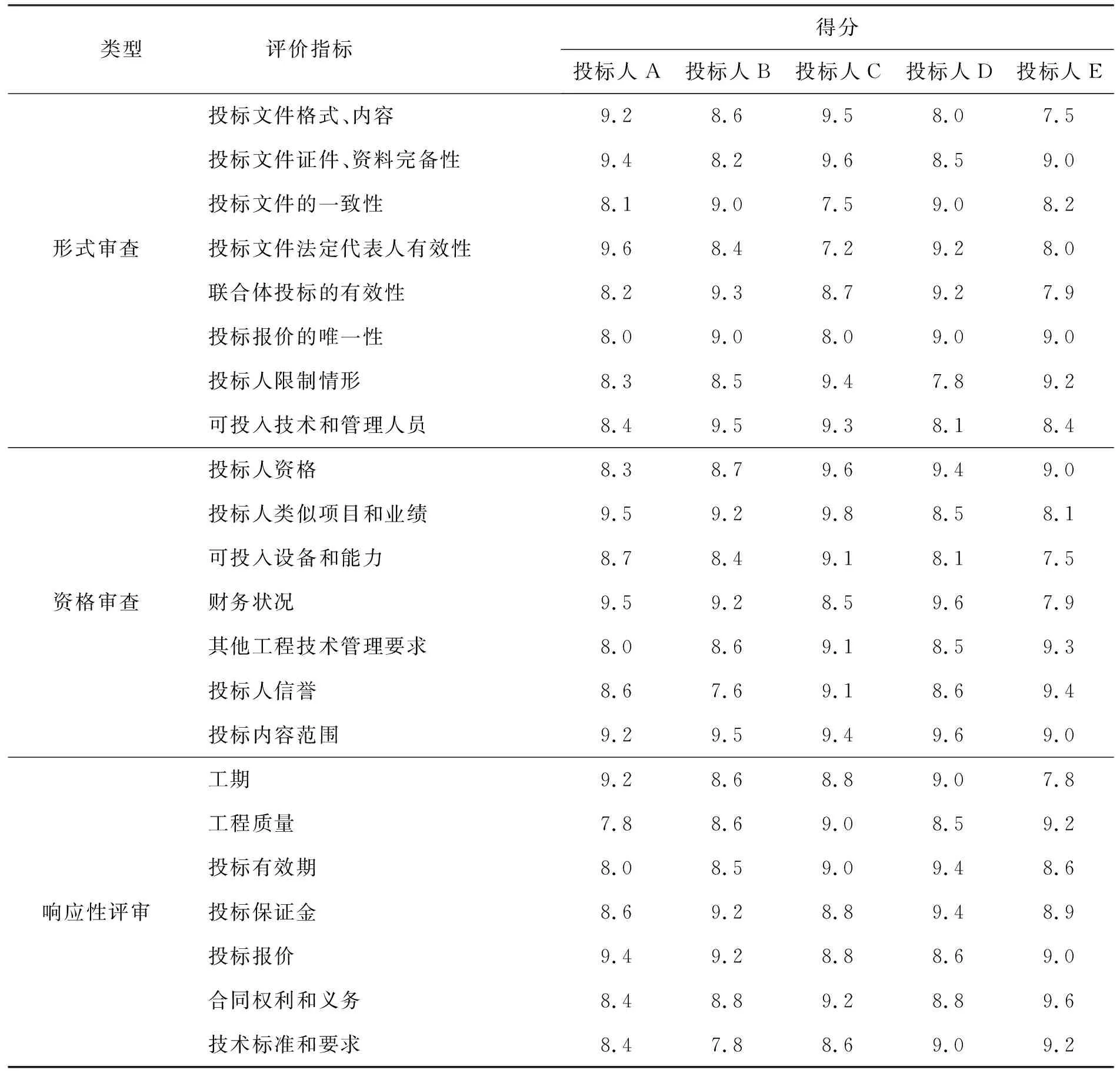
表1 投标人得分表

(二)物元模型的建立

1.确定经典域和节域

将投标人划分为3个等级，优、中、差，各等级物元的经典域分别为

节域物元为：

确定待评物元：

2.计算关联函数值

根据公式(4)、(5)、(6)计算各投标人关联函数值，如表2。

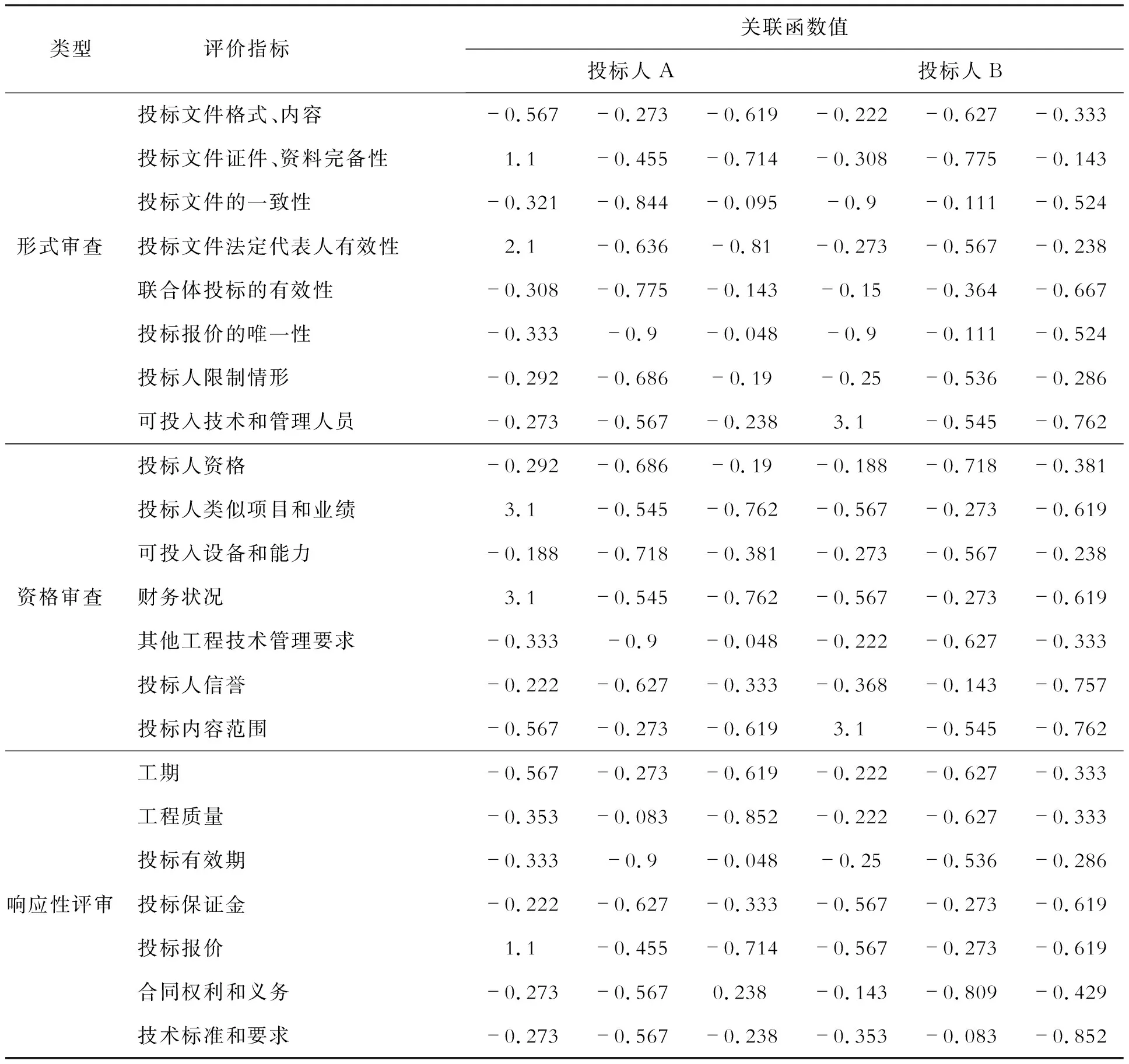
表2 投标人关联函数值表

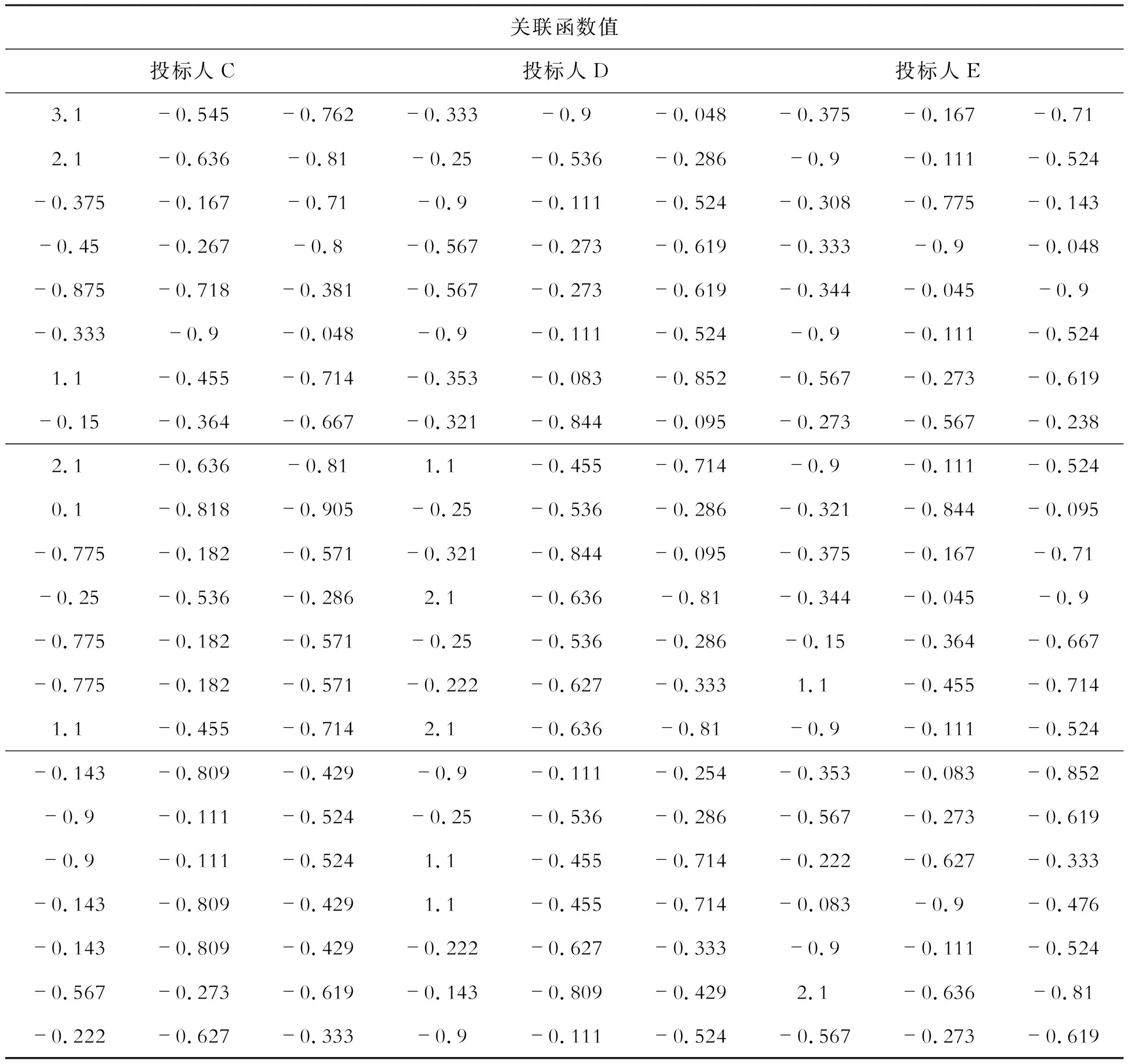
续表2

3．各评价指标熵权系数的确定

根据各评价指标对投标人的影响大小和公式(7)～(12)确定熵权，如表3。

表3 评价指标熵权系数表

续表3

4.计算各投标人综合得分

根据公式(13)计算各投标人综合得分。

KA=(0.088 7，-0.509，-0.420)，

KB=(-0.213，-0.462，-0.486)

KC=(-0.139，-0.508，-0.524)，

KD=(-0.104，-0.467，-0.428)

KE=(-0.217，-0.365，-0.586)

根据评价总则，投标商A综合得分与评价指标间关联性最好，为最佳选择。

三、结语

可拓学评价理论引入物元的概念，采用定性与定量相结合，利用物元的可拓性定性确定评价指标，对关联函数进行定量计算。通过建立物元模型将各个评价指标转化为一种相容的问题，特别是把实变函数中距离的概念拓展为距的概念，使得关联函数值域范围得到了拓展，把评价指标由单一的确定值转变为区间值，使评价对象和某衡量指标之间建立关联函数，寻找符合要求的对象。从而能更全面地评价投标人的优劣程度，最大限度客观评标，得出优选结果。

基于可拓理论构建评价物元模型，建立了评价指标与投标人专家评分之间的关联函数，计算得出关联度。相比综合评分法，此方法不仅在投标人确定方法上更好地实现了客观定量化，而且使评价指标与综合评价得分之间建立强关联关系，提高了评价指标对最终评标结果的贡献度。同时，利用计算所得关联度评价投标人，能更全面地评价投标人的优劣程度，进而使招投标管理的评标环节更加客观公正，避免了评标过程中主观确定投标人的弊端。