序贯拍卖中报价排序信息披露的研究

胡二琴，赵　勇，陈　莹

(1.华中科技大学系统工程研究所，湖北武汉430074；2.湖北工业大学理学院，湖北武汉430068；3.深圳大学经济学院，广东深圳518060)



序贯拍卖中报价排序信息披露的研究

胡二琴1，2，赵勇1，陈莹3

(1.华中科技大学系统工程研究所，湖北武汉430074；2.湖北工业大学理学院，湖北武汉430068；3.深圳大学经济学院，广东深圳518060)

研究了两场拍卖间报价排序的披露对投标人报价以及拍卖人收益的影响.首先，基于博弈理论分析了报价排序披露策略下投标人的均衡报价策略.其次，从投标人报价与拍卖人收益的角度将排序披露策略与获胜价、获胜者身份披露策略进行了比较.最后，比较了每种披露策略下两场拍卖间的拍卖人收益.结论表明：披露获胜者身份对拍卖人最有利；而披露报价排序时，投标人会通过降低第1场拍卖中的报价去换取第2场拍卖中的信息优势，从而导致拍卖人收益最低.

序贯拍卖；披露策略；报价排序；收益比较

1　引　言

由于定价灵活、交易自由和参与成本低等特点，网上拍卖近年来已成为商品销售与采购的一种重要渠道[1].中国拍卖行业协会发布的《2013年中国拍卖行业经营状况分析及2014年展望》指出，2013年是中国拍卖行业名副其实的“网上拍卖发展年”，网上拍卖成交金额超过200亿元.网上拍卖不受拍卖时间与空间的限制，交易双方在虚拟市场中相遇，双方间的信息不对称进一步加剧.与传统拍卖相比，网上拍卖中投标人面临更大的信息不确定性，而拍卖人则拥有更多关于拍卖品或市场竞争特性等对投标人有用的信息，拍卖人该不该披露、该如何披露这些信息一直是拍卖理论界与实践界关注的热点[25].

大量相同或相似的物品序贯售出，同一批投标人在多个市场阶段重复竞争是许多产品市场(如商品批发市场、药品采购市场)中的一类常见现象.在网络环境下，由于没有面对面接触，以ID代替真实身份进行交易，投标人通常并不清楚对手的人数、身份、价值或成本等信息.但是投标人拥有跨阶段学习的能力，仅从前期拍卖结束后披露出的获胜信息中也能推断出对手的一些信息，并用来规划后期的报价策略.拍卖人获胜信息的披露方式决定了投标人能获取从前期拍卖中获取多少信息.比如，若拍卖结束后披露所有报价，则投标人不仅可以观察到对手的人数，还可从报价中反推出所有对手的价值或成本信息.但是若拍卖人只是私下通知每个投标人是否获胜，则投标人对对手信息仍一无所知.而理性的投标人在前期拍卖中就会预期到信息披露效应，并调整报价策略以求获取对手的信息或者阻止对手获取自身信息.这使得投标人的报价策略不同于单场拍卖时的报价策略.拍卖人的收益显然也会受到影响.因此，在重复竞争环境下如何披露获胜信息也是拍卖机制设计的重要环节.针对网上序贯采购拍卖中供应商通常不清楚对手人数这一特点，Arora等[6]比较了披露获胜价与披露所有报价两种策略下的采购成本.而针对供应商不清楚对手成本类型这一特征，Thomas[7]，Kannan[8]和Timothy等[9]分别在供应商风险中立与风险厌恶的假定下，比较了披露获胜价与披露所有报价两种策略下的采购成本.在投标人不确定对手价值类型且胜者退出的假定下，Jeitschko[10]发现披露获胜价时投标人会在第1场拍卖中降低报价去获取对手信息(即抽取效应)，而Kannan[11]和Ding等[12]指出当披露所有报价时投标人在第1场拍卖中会冒充其他类型投标人以阻止对手获取自己的信息(即欺骗效应).这些研究主要分析了披露获胜价与披露所有报价这两种披露策略.而现实中可行的披露策略远不止这两种，而且披露报价往往会泄露投标人的价值或成本等重要信息，而在医药、高科技产品生产中这类信息的机密性是至关重要的.如美国药品采购拍卖结束后，只会披露获胜者身份.不披露具体报价、只披露报价排序也是近年来实际拍卖中被广泛采用的一种披露策略.但是目前关于排序披露策略的理论研究比较有限.Elmaghraby等[13]发现在单场公开采购拍卖中，与披露所有报价相比，披露报价排序使得供应商无法立即获取对手的完全信息，导致供应商失去耐心从而竞价更加激烈、采购成本更低.那么，在重复竞争环境下报价披露排序是否也能成为拍卖人的最优披露策略是一个尚待研究的问题.

本文分析了在序贯密封拍卖间披露报价排序时投标人的报价特征，并在文献[10]的基础上将报价排序披露策略与获胜价披露、获胜者身份披露这两种策略以及序贯第二价格密封拍卖进行了比较，旨在为拍卖人选择最优的拍卖方式、披露策略提供参考.进一步，比较了两场拍卖间的拍卖收益，能为拍卖人选择最优的拍卖时机提供一定的参考.

2　问题描述与相关概念

假定两个相同的物品拟通过两场第一价格密封拍卖来售出，每场拍卖中售出1个物品.3个具有独立私人价值的投标人参与竞拍，且下述信息为共同知识：

1)投标人对每个物品的价值v或为高价值vH或为低价值vL1一方面，离散的价值类型假定更贴合实际[14]；另一方面，当投标人价值类型为连续型时，由于对称性，投标人在第1场拍卖中采用的对称均衡报价为其价值的增函数，因此第1场拍卖结束后，报价排序的披露将使得投标人的价值排序成为共同知识，从而根据Landsberger[15]的研究可直接求解排序披露策略下的报价均衡..不失一般性，设vH=1，vL=0.每个投标人在拍卖前就知道自己的价值类型，且其价值类型在两场拍卖中保持不变2实际拍卖数据表明，短期内同质物品的序贯拍卖中，投标人价值的衰减速度较慢[16].；

2)投标人事前对称.每个投标人为高价值类型的概率为θ(0＜θ＜1)，为低价值类型的概率为1-θ；

3)拍卖人与投标人风险中立、均追求期望收益最大化.每场拍卖中，价值为v的投标人以报价b胜出时的收益为v-b，未胜出时的收益为0；

4)两场拍卖的公开保留价均为vL=03拍卖人知道投标人的最低价值后将其设为保留价，这个假定是合理的..第1场拍卖结束后，不披露具体报价只披露报价排序，报价最高者排在第1位且胜出，报价次高者排在第2位，以此类推.在报价相同时，通过抛硬币的方式来随机决定排序；

5)投标人具有单物品需求，第1场拍卖中排在第1位的投标人胜出、支付自己的报价并退出拍卖.

本文中投标人知道对手的人数，但不知道对手的价值类型.许多网上拍卖(如淘宝拍卖)均符合这一特征.本文中假定采用的是序贯第一价格密封拍卖，因为在序贯第二价格密封拍卖中探讨信息披露效应是无意义的.在序贯第二价格拍卖中，不论第1场拍卖结束后披露出何种信息，投标人在第2场拍卖中都会报出自己的真实价值，而在第1场拍卖中投标人的均衡报价为其价值减去其在第2场拍卖中的期望收益.因此可得，在序贯第二价格密封拍卖下，拍卖人在第1，2场拍卖中的期望收益分别为Φ1=3θ3-2θ4与Φ2=θ2.

下面介绍本文中涉及到的三个主要概念.

定义1设随机变量X与Y的分布函数分别为F(·)与G(·).若对∀x∈R，有F(x)≤G(x)，则称X是一阶随机占优于Y.

当X是一阶随机占优于Y时，必有E[X]≥E[Y].

定义2若在信号博弈的均衡中，不同类型的信号发送者选择不同的信号，因而信号接收者可通过接收到的信号准确判断出发送者的类型，这类均衡称为分离均衡；若在均衡中，不同类型的信号发送者都选择相同的信号，这类均衡称为混同均衡.

在保险市场中，若保费越高赔付率也越高，那么高风险人群将购买高保费高赔付的保单，而低风险人群将购买低保费低赔付的保单，这里实现的就是分离均衡.本文中，低价值投标人的均衡报价为0，若高价值投标人的均衡报价高于0，这类均衡即是分离均衡；若高价值投标人的均衡报价为0，这类均衡则是混同均衡.

混合策略是参与人对其他参与人所采取的行动具有不确定性时的一个理性对策.如在石头-剪刀-布游戏中，为了不让对手猜透自己的策略，参与人以各为1/3的概率随机选择出石头、剪刀或布.

3　均衡分析

低价值投标人的报价必为0，故只需分析高价值投标人的报价.两物品的序贯拍卖是个典型的两阶段博弈，我们利用逆向归纳法先求解第2场拍卖中的报价均衡.由于胜者退出，第2场拍卖是两个投标人参与的单场拍卖.引理1给出了这类拍卖中的报价均衡.

由引理1知，第2场拍卖中两个投标人的报价均衡取决于投标人的信念，而其信念又依赖于他们在第1场拍卖中的报价及信息披露策略.

定理1报价排序披露策略下，第1场拍卖中不存在混同均衡.

证明见附录.

下面考虑分离均衡.可证得，第1场拍卖中不存在对称的纯策略报价均衡.假设b为第1场拍卖中高价值投标人的对称均衡报价，0＜b＜1.当其他高价值投标人在第1场拍卖中按照此对称均衡报价时，某个高价值投标人递交一个略高于b的报价便可将获胜的概率从(1-θ)2+θ2/3+θ(1-θ)增大到1，因此偏离是有利的，这与b为均衡报价相矛盾.为了不让对手预测到自己的报价，高价值投标人采用混合策略，按照某分布在区间内随机报价[17].报价下限必为无穷小的正数.一方面/=0.因为报价为0时高价值投标人获胜概率仅为(1-θ)2/3，而递交一个略大于0的报价就能使得获胜的概率增大为(1-θ)2.另一方面必无限接近0.因为当高价值投标人递交一个更低的报价p(0＜p＜)时，他获胜的概率与报价为时的获胜概率相同，但收益更高，故高价值投标人可向下调整报价下限，直到无限接近0.设排序披露策略下，高价值投标人在第1场拍卖中的报价分布为(b)，b∈(0].

3.1第2场拍卖的均衡分析

在第2场拍卖中，低价值投标人报价为0，高价值投标人根据自身在第1场拍卖中的报价、排序以及贝叶斯公式修正关于对手价值类型的信念并调整报价.记第1场拍卖中排在第2、3位的投标人分别为S与T，他们在第1场拍卖中的报价分别为bS，bT，则bS≥bT.若T为高价值类型，则T认为对手S为高价值类型的概率为β=1.若S为高价值类型，则S认为对手T为高价值类型的概率为

其中vT为T的价值.显然，α＜θ.

值得注意的是，因为只披露出报价排序信息而没有披露具体的报价，所以S与T的信念α，β不再是共同知识而是他们各自的私人信念，这是报价排序披露策略的最大特点.

定理2报价排序披露策略下，第2场拍卖的一个报价均衡如下：若为低价值类型，投标人报价为0；若为高价值类型，投标人T的报价与期望收益分别为

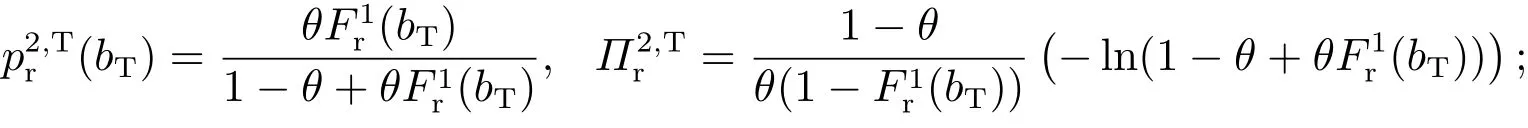
高价值投标人S在区间(0，α]内随机报价，其报价分布与期望收益分别为

证明见附录.

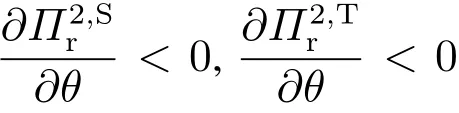
3.2第1场拍卖的均衡分析

投标人在第1场拍卖中的报价不仅决定了自身在第1场拍卖中的胜负与收益，也决定着自身在第2场拍卖中的信息及期望收益.考虑到信息披露的影响，理性的投标人在第1场拍卖中就会调整报价以最大化两场拍卖中的总期望收益.

定理3报价排序披露策略下，第1场拍卖中存在分离均衡：若为低价值类型，投标人报价为0；若为高价值类型，投标人在区间(0]内随机报价，其均衡报价分布满足下式4式(1)的解有两支，选取上方那一支以确保(·)为分布函数.，即

证明见附录.

综上所述，排序信息的披露将导致第2场拍卖中投标人信息不对称，排在第3位的高价值投标人可以获取对手的完全信息，而排在第2位的投标人S对对手的价值类型仍具有不确定性，且S在第1场拍卖中报价越低，他在第2场拍卖中信息越明确.这会激励着投标人在第1场拍卖中降低报价，从而影响拍卖人的收益.为了进一步分析报价排序信息的披露对拍卖人收益的影响程度并探讨拍卖人最优披露策略的选取，有必要将排序披露策略与其他披露策略进行比较.

4　信息披露策略的比较

披露获胜者身份与披露获胜价是实际拍卖中常采用的两种披露策略.获胜者身份披露策略下，拍卖人只公布获胜者身份、或私下告知每个投标人是否胜出.而在获胜价披露策略下，拍卖人只披露获胜价.本节将报价排序披露策略与获胜价披露策略、获胜者身份披露策略进行了比较，并将这3种披露策略分别简记为r，w和c，并记披露策略s(s∈｛r，w，c｝)下拍卖人在第t(t=1，2)场拍卖中的期望收益为其中高价值投标人在第1场拍卖中的策略性报价行为及其对拍卖人收益的影响是比较的重点.

获胜价披露策略下，第1场拍卖中获胜价的披露不仅使获胜者的价值类型成为共同知识，也使第2场拍卖中投标人的价值信念成为共同知识.设披露获胜价时，高价值投标人在第1场拍卖中的报价分布为(b)，其中bw为第1场拍卖中的获胜价，则第2场拍卖中投标人认为对手为高价值类型的概率为显然，θL＜θ.而在获胜者身份披露策略下，第2场拍卖中的投标人认为对手为高价值类型的概率仍为θ.根据引理1，易得下述引理.

引理2[10]获胜价披露策略下，第1，2场拍卖中高价值投标人的报价分布分别为

由引理2可得，获胜价披露策略下拍卖人在第1，2场中的期望收益分别为

引理3[10]获胜者身份披露策略下，第1，2场拍卖中高价值投标人的报价分别为

由引理3得，获胜者身份披露策略下拍卖人在第1，2场中的期望收益分别为

由此可得，获胜者身份披露策略下的拍卖人收益与序贯第二价格密封拍卖中的拍卖人收益相同.

定理4第2场拍卖中，获胜者身份披露策略下拍卖人期望收益最高，而高价值投标人期望收益最低.

证明见附录.

定理4成立的一个直观原因在于第2场拍卖中投标人关于对手价值类型信念的差异.披露获胜者身份后，投标人认为对手为高价值类型的概率仍为θ；而披露获胜价后，投标人认为对手为高价值类型的概率下降为θL，披露报价排序后，排在第2位的投标人S认为对手T为高价值类型的概率下降为α.故与披露获胜者身份相比，披露获胜价或披露报价排序后，投标人认为第2场拍卖中的对手更弱，因此报价更低.披露报价排序时，虽然排在第3位的投标人T认为对手S为高价值类型的概率上升到1，但是预期到S乐观的信念后T也会降低报价.因而，披露获胜者身份时，投标人报价最高从而拍卖人收益也最高.

下面比较第1场拍卖中高价值投标人的报价.分别取θ=0.3，0.5，0.7，0.9，通过数值模拟绘图(图1)发现定理5证明了对∀θ∈(0，1)，都有成立.

定理5对∀θ∈(0，1)，高价值投标人在第1场拍卖中的报价分布均满足

证明见附录.

结合定义1知，披露获胜者身份时高价值投标人在第1场拍卖中的平均报价最高，而披露报价排序时平均报价最低.其原因在于获胜价或排序信息的披露为投标人提供了降低报价的激励：其一，由于第1场拍卖中的获胜者将退出第2场拍卖，因此在制定第1场拍卖中的报价策略时，投标人必然会考虑到赢得第1场拍卖的机会成本(即退出第2场拍卖后，无法在第2场拍卖中获得的期望收益).由定理4知，披露获胜价或排序信息时，这种机会成本要高于披露获胜者身份时的机会成本，因此获胜价或排序披露策略下，高价值投标人将降低第1场拍卖中的报价；其二，披露获胜价时，高价值投标人在第2场拍卖中的期望收益是第1场拍卖的获胜价的减函数，这也激励着投标人在第1场拍卖中降低报价；而在排序披露策略下，这种激励被进一步扩大，因为由定理2知，高价值投标人在第2场拍卖中的期望收益是第1场拍卖中自身报价而非获胜价的减函数；其三，披露获胜价时，第1场拍卖中的获胜价越低，第2场拍卖中投标人信息越明确；而在排序披露策略下，投标人在第2场拍卖中的信息取直接决于自身在第1场拍卖中的报价，第1场拍卖中排在第3位的高价值投标人具有信息优势、能确切知道对手的价值类型.而第1场拍卖中的报价越低，排在第2位的投标人在第2场拍卖中的信息越明确，这鼓励着投标人通过降低第1场拍卖中的报价去获取第2场拍卖中的信息优势.而获胜者身份披露策略下，投标人无法通过第1场拍卖中的报价影响第2场拍卖中的信息与期望收益因而阻断了投标人的策略性信息获取行为.因此，在第1场拍卖中，披露获胜者身份时高价值投标人报价最高，披露报价排序时投标人降低报价的激励最大，从而报价最低.由此可得，获胜者身份披露策略对拍卖人最有利.

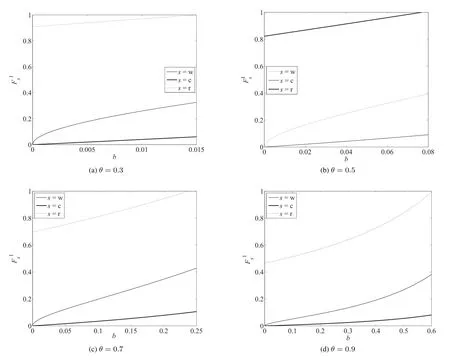
图1　3种披露策略下高价值投标人在第1场拍卖中的报价分布Fig.1 The bidding distributions of high-value bidders in the 1st auction under three information revelation policies

定理6第1场拍卖中，披露获胜者身份时拍卖人的期望收益最高，而披露报价排序时拍卖人的期望收益最低.

结合定理4、定理6可知，在这种重复竞争环境下，披露获胜者身份对两场拍卖中的拍卖人均是最优的.

在实际的序贯拍卖中，每场拍卖的拍卖人可能不是同一人.第1场拍卖中拍卖人披露策略的选择不仅影响着自身的收益也影响着后续拍卖人的收益，那么不同拍卖人的收益间是否存在差异呢？为此，本文对获胜价披露策略与获胜者身份披露策略下两场拍卖中的拍卖人收益进行了比较.记∆s为披露策略s(s∈｛c，w｝)下两场拍卖中拍卖人的收益差，则

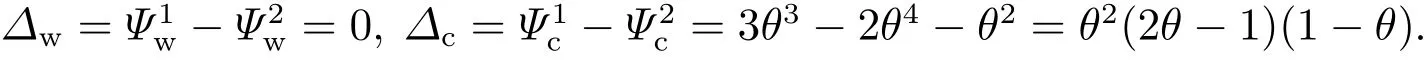
因此可得，获胜价披露策略下，拍卖人收益具有鞅性质，两场拍卖中的拍卖人收益无差异.而获胜者身份披露策略下，当θ＜0.5时，第1场拍卖的拍卖人收益低于第2场拍卖中的拍卖人收益且θ=0.3时两者收益差最大；而θ＞0.5，第1场拍卖中的拍卖人收益高于第2场拍卖中的拍卖人收益且θ=0.82时两者收益差最大.

5　结束语

本文研究了序贯拍卖中两场拍卖间报价排序信息的披露对投标人报价以及拍卖人收益的影响，进而探讨了获胜信息的最优披露策略，得到了以下结论.首先，获胜者身份披露策略与第二价格密封拍卖机制均能阻断投标人在两场拍卖间的策略性信息行为，对两场拍卖中的拍卖人都是最有利的.其次，在序贯拍卖中后续拍卖人的收益受到前期拍卖披露策略的影响.当前期拍卖采取了非最优的披露策略时，后续拍卖人可通过选择第二价格拍卖来消除前期披露出的信息的影响，增加自身的收益.最后，当拍卖人之间存在竞争时，拍卖人何时进入拍卖市场最有利依赖于拍卖形式、获胜信息的披露策略以及市场竞争强度.这些结论能为拍卖人的拍卖方式、信息披露策略以及交易时机的选取提供一定的实用性建议.

本文假定只有3个投标人，基于本文的分析可知，当投标人超过3人时相关结论也成立.理论研究中，投标人被假定为完全理性、能够从披露出的信息中修正获取对手的信息，而在实际中完全理性的要求过高，导致理论结论与实际情况通常存在一定的偏差.今后的工作是通过开展行为实验去探索不同披露策略下实际投标人的报价特征，检验本文的结论.

[1]陈剑，陈熙龙，宋西平.拍卖理论与网上拍卖.北京：清华大学出版社，2005. Chen J，Chen X L，Song X P.Auction Theory and Online Auction.Beijing：Tsinghua University Press，2005.(in Chinese)

[2]赵勇，陈阳，饶从军.一种信息优势的比较和拍卖机制研究.管理科学学报，2009，12(6)：90-99. Zhao Y，Chen Y，Rao C J.Research on information superiority and auction mechanism.Journal of Management Sciences in China，2009，12(6)：90-99.(in Chinese)

[3]侯晶.供应风险下后备采购中的信息共享价值研究.系统工程学报，2013，28(5)：668-676. Hou J.Value of information sharing in backup sourcing under supply risks.Journal of Systems Engineering，2013，28(5)：668-676. (in Chinese)

[4]Anand K S，Goyal M.Strategic information management under leakage in a supply chain.Management Science，2009，55(3)：5438-5452.

[5]Szech N.Optimal disclosure of costly information packages in auctions.Journal of Mathematical Theory，2011，47(4-5)：462-469.

[6]Arora A，Greenwald A，Kannan A.Effects of information revelation policies under market structure uncertainty.Management Science，2007，53(8)：1234-1248.

[7]Thomas C J.Information revelation and buyer profits in repeated procurement competition.The Journal of Industrial Economics，2010，58(1)：79-105.

[8]Kannan K N.Effects of information revelation policies under cost uncertainty.Information Systems Research，2012，23(1)：75-92.

[9]Timothy N C，Karthik N K，Ralph S.An experimental study of information revelation policies in sequential auctions.Management Science，2011，57(4)：667-688.

[10]Jeitschko T D.Learning in sequential auctions.Southern Economic Journal，1998，65(1)：98-112.

[11]Kannan K N.Declining prices in sequential auctions with complete revelation of bids.Economics Letters，2010，108(1)：49-51.

[12]Ding W，Jeitschko T D，Wolfstetter G E.Signal jamming in a sequential auction.Economics Letter，2010，108(1)：58-61.

[13]Elmaghraby W J，Katok E，Santamara N.A laboratory investigation of rank feedback in procurement auctions.Manufacturing and Service Operations Management，2012，14(1)：128-144.

[14]Lambson V，Thurston N.Sequential auctions：Theory and evidence from the Seattle fur exchange.Rand Journal of Economics，2006，37(1)：70-80.

[15]Landsberger M，Rubinstein J，Wolfstetter E，et al.First-price auctions when the ranking of valuations is common knowledge.Review of Economic Design，2001，6(3/4)：461-480.

[16]Fevrier P.He who must not be named.Review of Economic Design，2003，8(1)：99-119.

[17]Rasmusen E B，Janssen M.Bertrand competition under uncertainty.Journal of Industrial Economics，2002，50(1)：11-21.

附录

定理1的证明

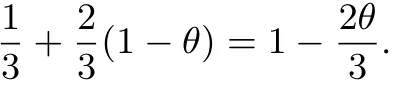
定理2的证明

证明均衡是参与人的一种策略组合，使得每个参与人的策略是对其他参与人策略的最优反应.

因此

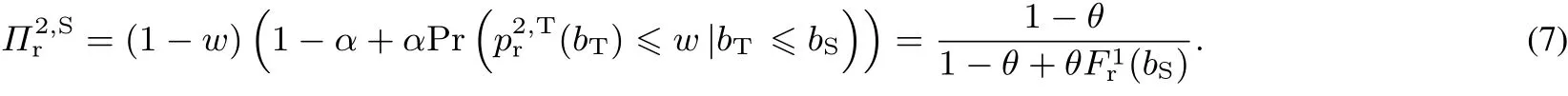
由式(7)可得，当w∈(0，α]时，S在第2场拍卖中的期望收益与w无关，只依赖于S在第1场拍卖中的报价bS，因此S可在(0，α]内随机报价.

定理3的证明

证明1)以高价值投标人A为例.设A在第1场拍卖中的报价为b.A在第1场拍卖中能排在第1位当且仅当其对手要么是低价值投标人，要么是报价低于b的高价值投标人，因此A能排在第1位胜出的概率为，其收益为1-b.A能排在第2位当且仅当其中一位对手为报价高于b的高价值投标人，而另一位对手要么是低价值投标人、要么是报价低于b的高价值投标人，因此A排在第2位的概率为，此时A在第2场拍卖中的期望收益为A能排在第3位当且仅当两位对手均为报价高于b的高价值投标人，因此他排在第3位的概率，此时A在第2场拍卖时的期望收益为

因此当A在第1场拍卖中报价为b时，A在两场拍卖中的总期望收益为

因为A在第1场拍卖中采用混合策略，因此报价为(0，ā]内的任一值时的期望收益应相等.由此可得

2)上述分析中先假定第1场拍卖存在分离均衡，后求解高价值投标人的报价分布下证的确为分离均衡.

若p＜θ，则A在第2场拍卖中的期望收益为

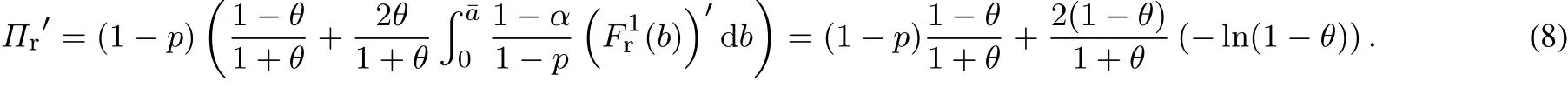
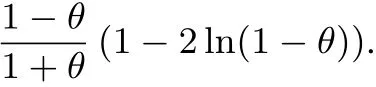
因此当在第1场拍卖中偏离分离均衡、报价为0时，A在两场拍卖中的总期望收益为

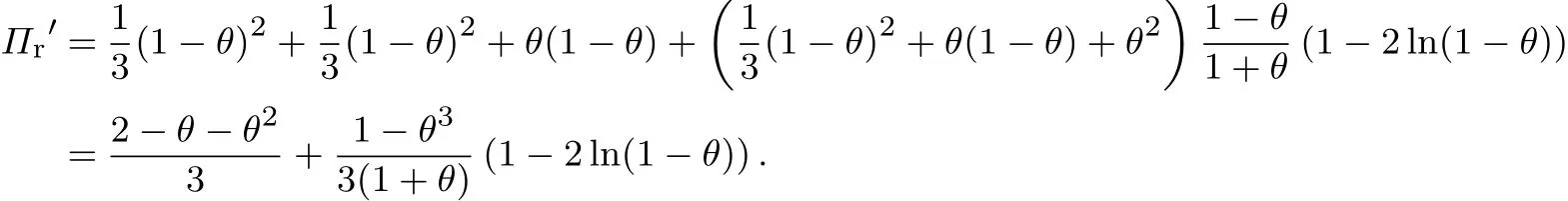
定理4的证明

证明由定理2、引理2以及引理3知，获胜者身份与获胜价披露策略下高价值投标人在第2场拍卖中的期望收益分别为而排序披露策略下第1场拍卖中排在第二、三位的买者在第2场拍卖中的期望收益分别为

在第2场拍卖中，若所有投标人都是低价值类型，则拍卖人收益为0；若存在一个高价值投标人，则三种披露策略下都是高价值投标人获胜，此时拍卖人与投标人期望收益之和为1.由此可得，高价值投标人收益越高，则拍卖人的期望收益越低.因此，获胜者身份披露策略下，拍卖人在第2场拍卖中的期望收益最高.证毕.

定理5的证明

若b＞θ2，则因此成立.

将式(1)变形可得

式(9)减去式(10)得

结合-式(11)可得，若b∈(0，θ2+θ(1-θ)ln(1-θ)]，则若因此，

Study of bids’ordinal ranks information disclosure in sequential auctions

Hu Erqin1，2，Zhao Yong1，Chen Ying3
(1.Institute of Systems Engineering，Huazhong University of Science and Technology，Wuhan 430074，China；2.School of Science，Hubei University of Technology，Wuhan 430068，China；3.School of Economics，Shenzhen University，Shenzhen 518060，China)

This paper explores the impacts of revealing bids’ordinal ranks between auctions on the bidders’bids and the auctioneers’revenues.Firstly，based on game theory，bidders’bidding strategies under rank revelation policies are analyzed.Then，rank revelation policies are compared with the winner’s identity revelation policies and the winning price revelation policies from the perspective of both bidders’bids and the auctioneers’revenues.Finally，the auctioneers’revenues in two auctions are compared under each revelation policies. The results show that it is most favorable for auctioneers to reveal only the winner’s identity.Under rank revelation policies，the bidders lower their first-stage bids to exchange for second-stage information advantage.As a result，the auctioneers gain the lowest revenues.

sequential auctions；disclosure strategy；bids’ordinal ranks；revenues comparison

F062.5

A

1000-5781(2016)03-0317-11

10.13383/j.cnki.jse.2016.03.004

胡二琴(1980-)，女，湖北黄冈人，博士生，讲师，研究方向：拍卖机制设计与博弈论，Email：hutu1980336@163.com；

赵勇(1967-)，男，湖北天门人，博士，教授，博士生导师，研究方向：决策分析，Email：zhiwei98530@sohu.com；

陈莹(1980-)，女，广东湛江人，博士，讲师，研究方向：资产定价，行为金融，Email：cying@szu.edu.cn.

2014-05-07；

2015-12-27.

国家自然科学基金资助项目(61273206；71201064)；湖北省教育厅科研基金资助项目(Q20131405).