污染环境中具有常数捕获率Gallopin系统的生存分析

许立滨，尹 晓

(哈尔滨理工大学应用科学学院，哈尔滨150080)

当今世界环境污染已经严重威胁种群的生存，研究污染对生态系统的影响是一个非常重要的课题，关于这方面的问题，已有很多结果.除此之外，人为的捕获对生物种群的发展也有着重要的影响.

在环境容纳量较大的情况下，何泽荣，马知恩研究了污染和常数捕获对单种群Logistic模型的影响[1].在环境容纳量较小的情况下，冯由玲等研究了污染和连续捕获对单种群Logistic模型持续生存和绝灭的影响对于资源-消费者模型[2]，马知恩，宋保军讨论了一类Gallopin资源-消费者模型，在小容量情况下，得到了消费者种群弱平均持续生存和绝灭的阈值[3].何泽荣，马知恩进一步考虑种群个体从环境中直接或间接地吸入毒素，以及个体向环境排毒作用的Gallopin模型，给出了种群弱平均持续生存和绝灭的判据，在一定条件下得到了阈值[4-5].本文在文献[4]的基础上考虑死亡种群将体内毒素带回环境，以及常数捕获对种群的影响，建立了污染环境中具有常数捕获的Gallopin系统.

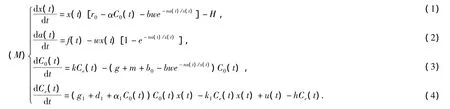
其中:x(t)，a(t)，C0(t)，Ce(t)分别表示t时刻的消费者的种群密度、资源量密度、种群个体体内毒素浓度、环境毒素浓度;r0=b0-d0是种群没有毒素时的自然增长率为种群的出生率为种群的死亡率;H是人为对消费者种群的捕获量;f(t)为资源的自然增长率，它为[0，∞)上的正值连续函数;表示由于排泄、新陈代谢以及种群死亡而带出种群内部的毒素表示种群从环境中吸收的毒素)表示由于种群排泄以及死亡而带入环境中的毒素;u(t)为外界向环境的毒素输入率;hCe(t)是表示人为的净化率r0、α、b、w、n、k、g、m、b0、d1、g1、k1、h、H均为正的常数，且满足关系

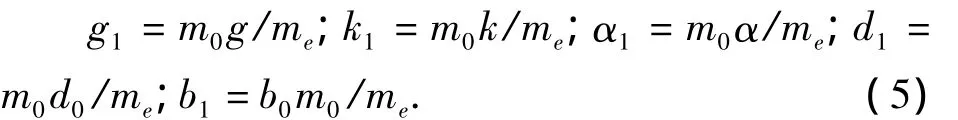
(m0为种群内每个个体的平均质量;me为环境内介质的总质量).

1 预备知识

定义1对给定数β＞0，x(0)＞β.若对一切t∈[0，+∞)，有x(t)＞β，则称种群x(t)是 β生存的.若存在T∈[0，+∞)，使得x(T)=β，则称种群x(t)是β绝灭的.

定义2对t0∈[0，+∞)，若存在T＞t0，使x(T)=0，则称种群x(t)是在有限时间内零绝灭.

对系统(M)做如下假设:

(H1)系统(M)初值

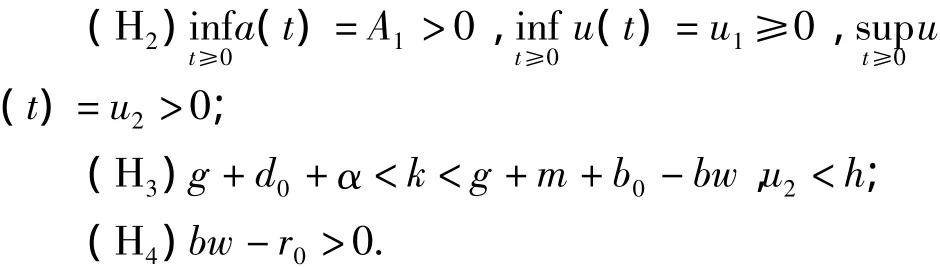
引理1对系统(M)，若满足(Hi)(i=1，2，3，4)及，则，有

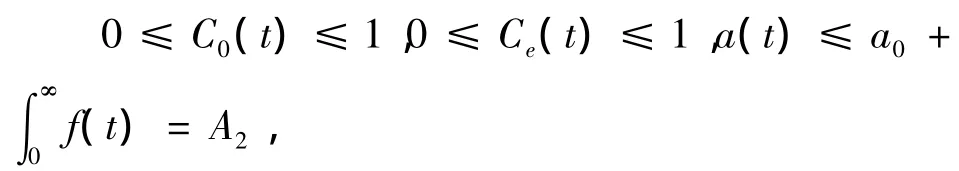
此外，若nbwA2-H＞0，存在T＞0，当t＞T时

证明 由式(3)，(4)知，

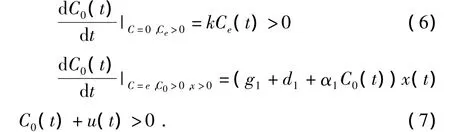
由假设(H1)和式(6)、(7)知，C0(t)≥0，Ce(t)≥0.

对于情形(1)，由式(3)和(H2)假设可知.

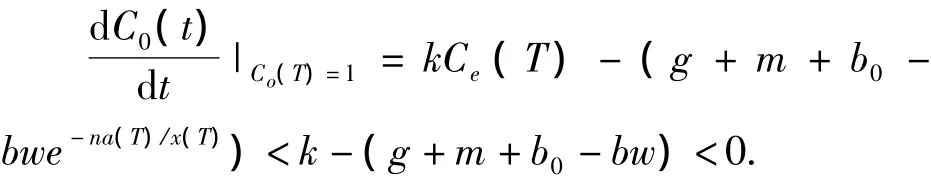
因此存在 δ＞0，使得t0∈[T，T+δ]，有Ce(t)＜1，C0(t)≤1.这与[0，T]的定义相矛盾，故不存在这样的T.同理可证情形(2)不成立.

对于情形(3)，由式(5)和(H3)可知从而由式(4)知

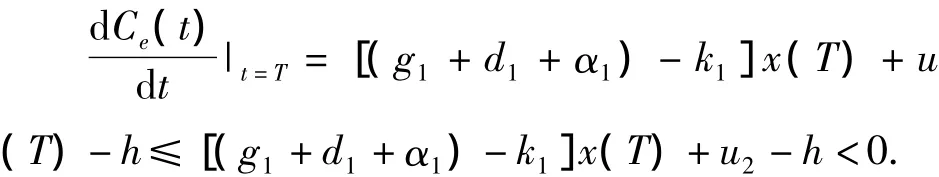
因而就保持C0(t)≤1，Ce(t)≤1的t而言，区间[0，T]仍可以向右延拓，这与T的性质矛盾，所以 不存在这样的T.故任意t∈R+，有0≤C0(t)≤1，0≤Ce(t)≤1.

再由式(1)和(H2)知

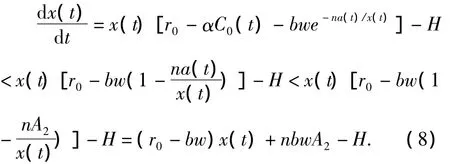
运用比较原理得

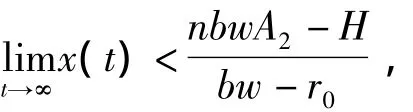
即对任意 ε ＞0，存在T，当时t＞T，有

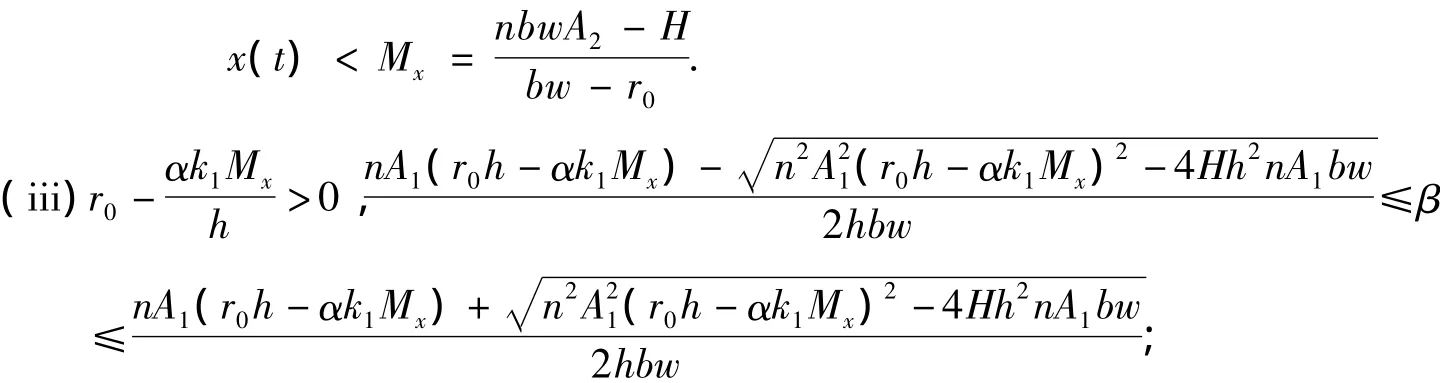
则种群x(t)是β生存的.其中Mx如引理1所示

即

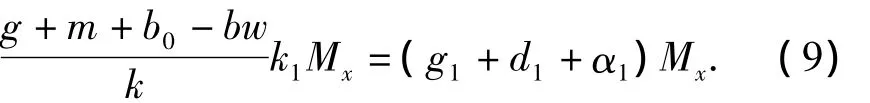
由系统(M)中的式(4)和引理1知

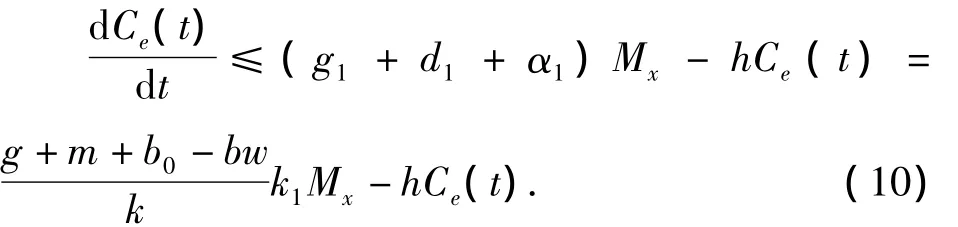
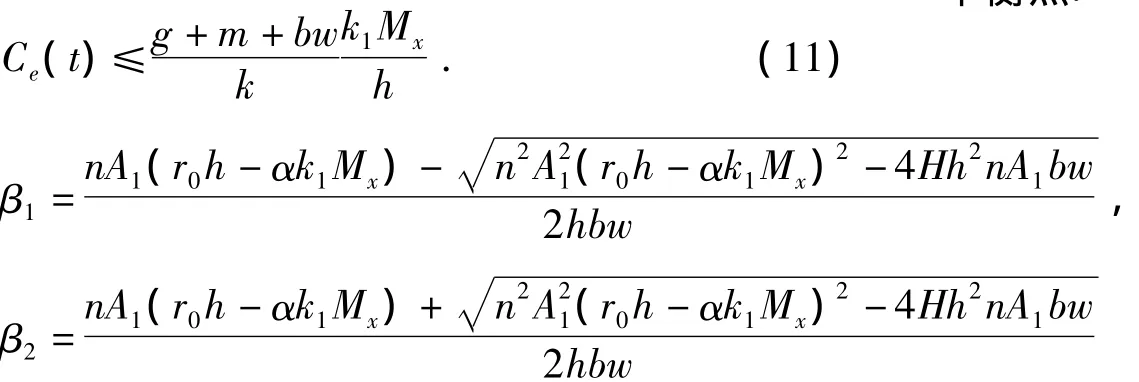
由定性分析和图1可知，β1不稳定点，β2是稳定点，则有证毕.

2 主要结果

定理1若系统(M)满足(Hi)(i=1，2，3，4)及

由式(11)和式(3)知

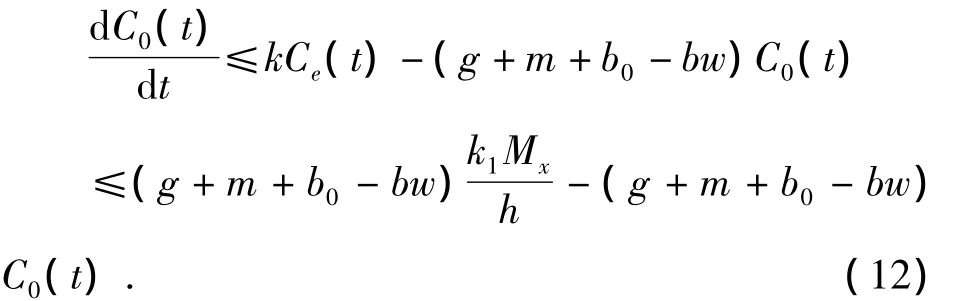
同理由(i)对式(12)利用比较原理知

再由式(1)和式(13)知

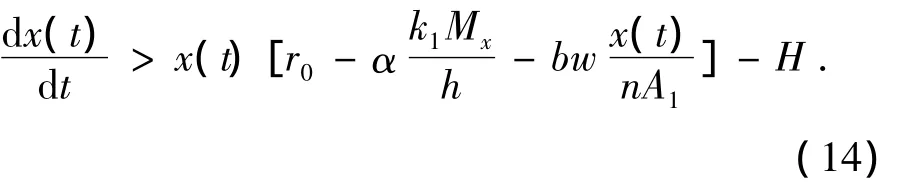
考虑式(14)的比较系统

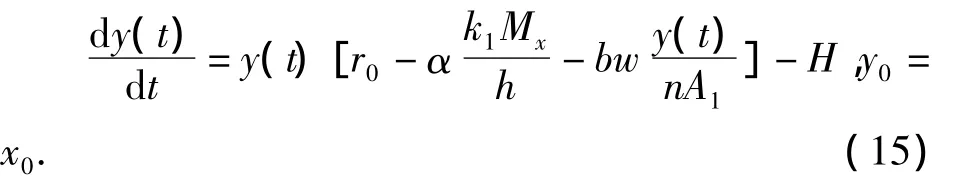
由二次函数的性质可知式(15)有如下两个正平衡点.

若y0＞β，则对任意t∈R+，y(t)≥β.

由比较原理可得

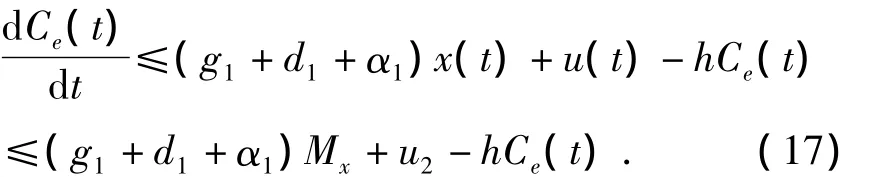
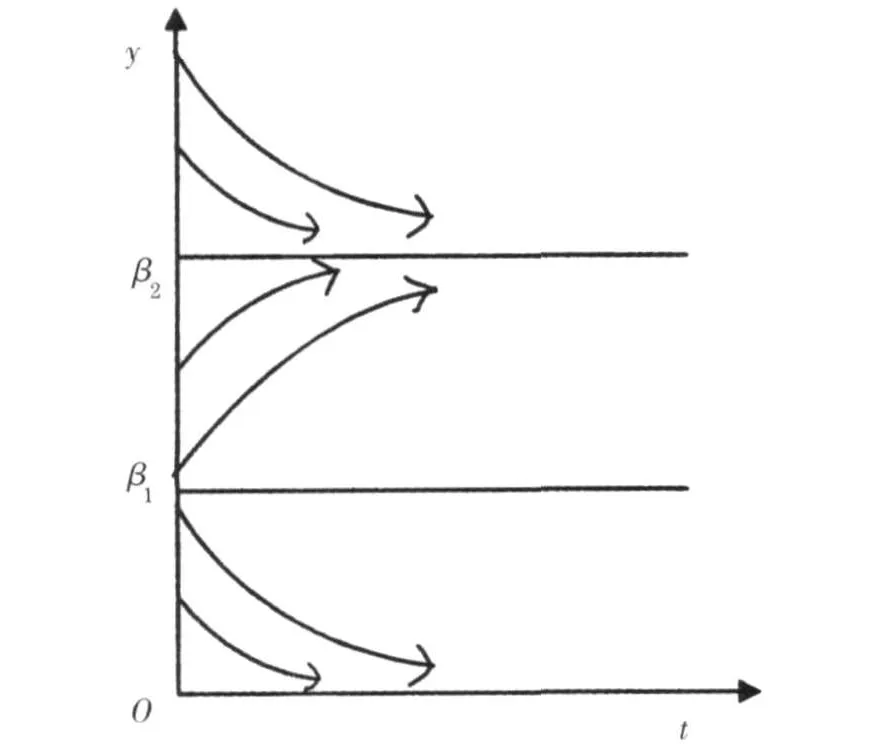
图1 系统(15)的积分曲线

由(ii)和(Hl)，对式(17)利用比较原理知

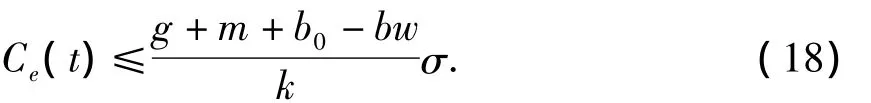
由式(3)和式(18)知

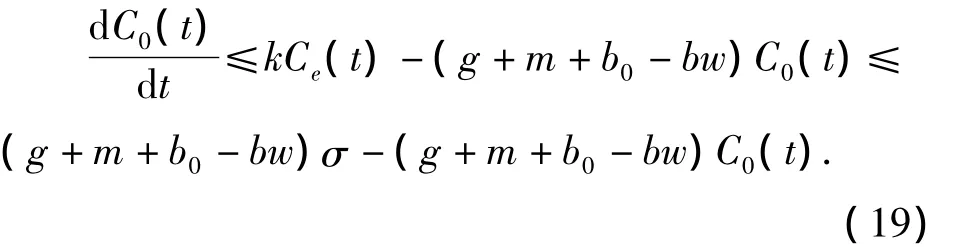
对式(19)利用比较原理知

再由式(1)和式(20)知

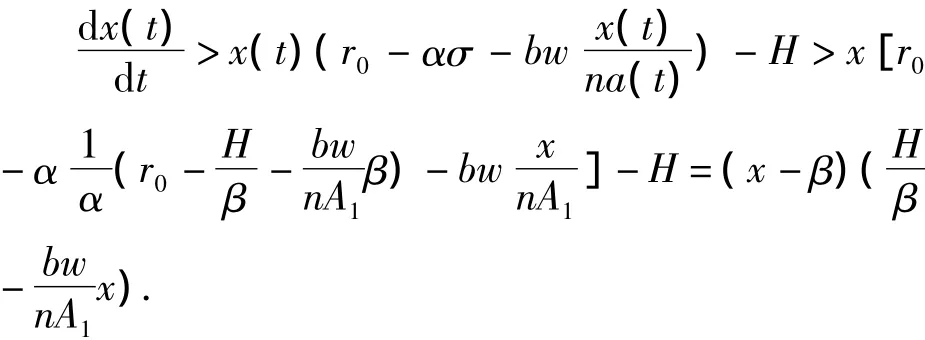
考虑比较系统

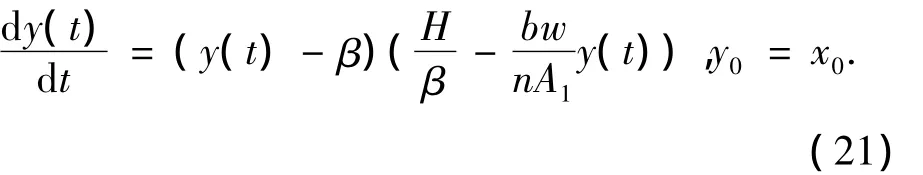
利用比较原理

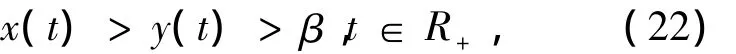
由式(15)和式(21)及定义1知结论成立，证毕.

证明 考虑式(8)的比较系统

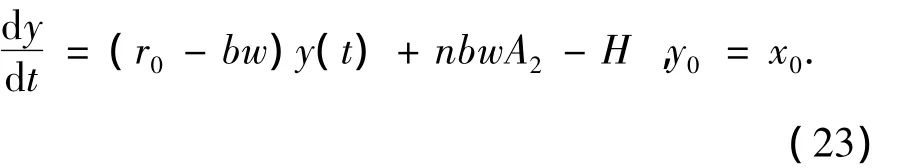
而已知有x0＞β，由函数的连续性可知，存在T＞t0，x(T)=β.由定义1知结论成立，证毕.

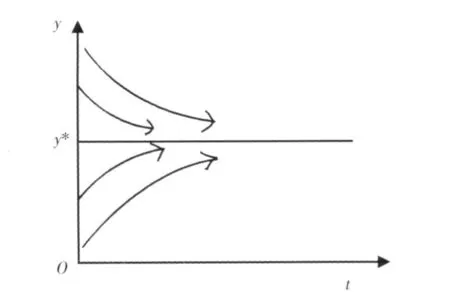
图2 系统(23)的积分曲线

证明 由式(4)及引理1知

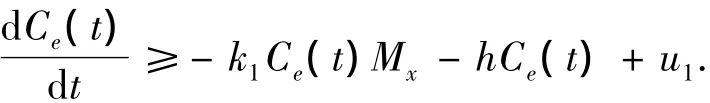
由比较原理，存在T1＞T，当t＞T1时，有

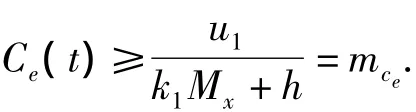
当t＞T1时，由式(3)知

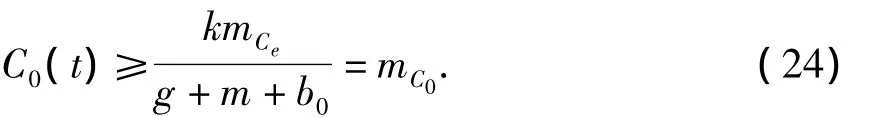
当时t＞T2，由式(1)及式(23)知

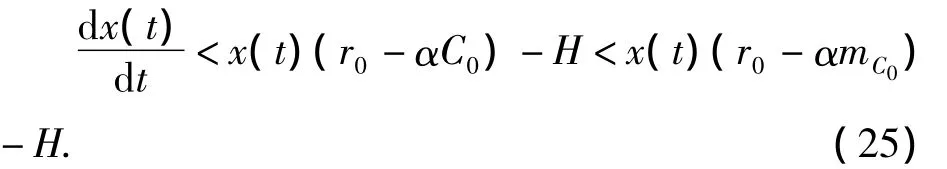
考虑(24)的比较系统

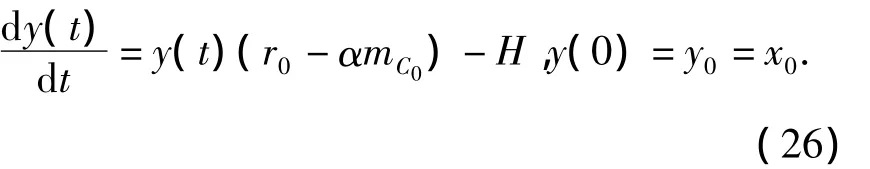
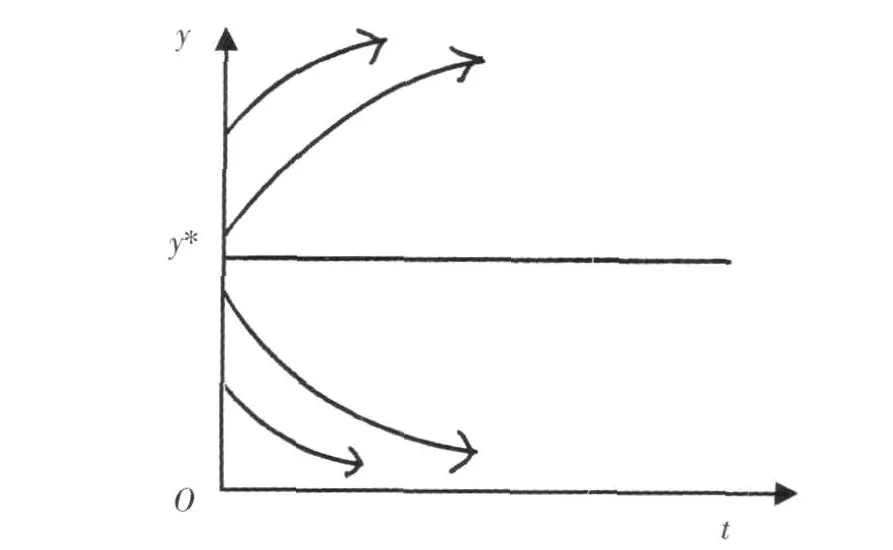
图3 系统(26)的积分曲线

3 结语

当种群个体体内毒素c0(0)和环境毒素的ce

(0)以及外界向环境输入的毒素的最大值u2满足定理1的条件时，可知种群x(t)是β生存的.由此人们捕获量H应控制在

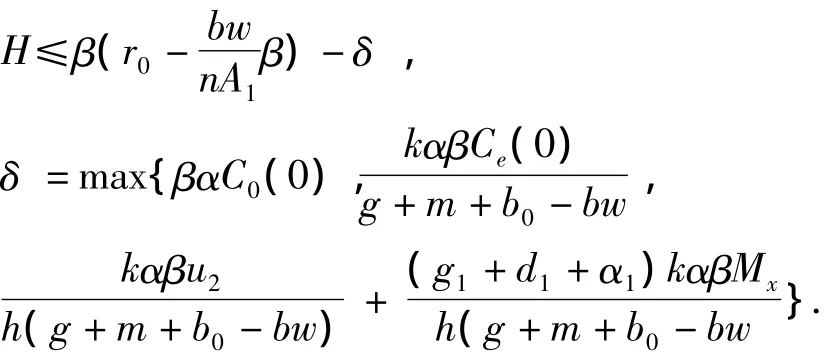
才能保证种群β生存的.

[1]何泽荣，马知恩.污染与捕获对Logistic种群的影响[J].生物数学学报，1997，12(3):230-237.

[2]冯由玲，王 克，孙静懿.具污染与捕获的Logistic单种群的持续生存及绝灭[J].生物数学学报，2006，21(3):365-369.

[3]MA Z E，SONG B J，HALLAM T G.The threshold between persistence and extinction of a population in a pollutied environment[J].Bull Math Biol.，1989.51(3):311-323.

[4]何泽荣，马知恩.污染环境中Gallopin系统的生存分析[J].应用数学和力学，2000，21(8):830-835.

[5]BUONOMO B，LIDDOA D，SGURA I.A diffusive-convective model for the dynamics of population-toxocant intentions:some analytical and numerical results[J].Math Bios.，1999，157(1):37-64.

[6]程亚焕，李冬梅.污染与捕获条件下一类广义Logistic种群的生存分析[J].哈尔滨理工大学学报，2004，9(6):119-121.