基于Voronoi图的空间区域划分算法

2011-10-17刘润涛

哈尔滨商业大学学报（自然科学版） 2011年6期

董雪，刘润涛

(哈尔滨理工大学应用科学学院，哈尔滨150080)

区域划分在计算几何、计算机图形学以及地理信息系统等许多领域有着广泛的应用.区域划分比较普遍的方法有两种[1]:一是人机交互实现对区域划分，需要人工将各个区域划分输出.二是通过图形识别及智能化方法对区域划分，这种方法也需要输入区域边界的相关数据，然后将划分后的封闭的子区域输出.由于第二种方法减少了许多人工的操作，而且输出结果更加精确，因此得到了广泛的研究.Voronoi图[2-3]是一个重要的计算几何分支，在计算几何理论和应用中起着非常重要的作用在计算几何中，Voronoi图的理论有效地来解决最近点的查找、求最大空圆、求最小树、求n个平面点的凸包等问题.王新生等采用网络Voronoi图研究城市网点的市场区域划分[4].王新生等用若干条折线将平面区域划分成若干子区域，提出一种平面区域划分的拓扑算法，加快了算法的运行速度.Tomasz对于空间划分给予过分析，但没有详细的算法分析.本文就是利用Voronoi图划分空间区域，定义了一个单位覆盖空间，并将分块区域内的点集标记颜色，位于同一分块内的点有相同的特性，从而把平面或维空间划分为有周期性或准周期性的分块[5].

1 基本概念

点的集合，将由

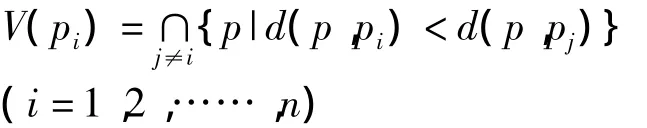
对平面进行分割，称为以pi(i=1，2，……，n)为生成元(或母点)的Voronoi图，区域V(pi)被称为pi的Voronoi区域，见图1.

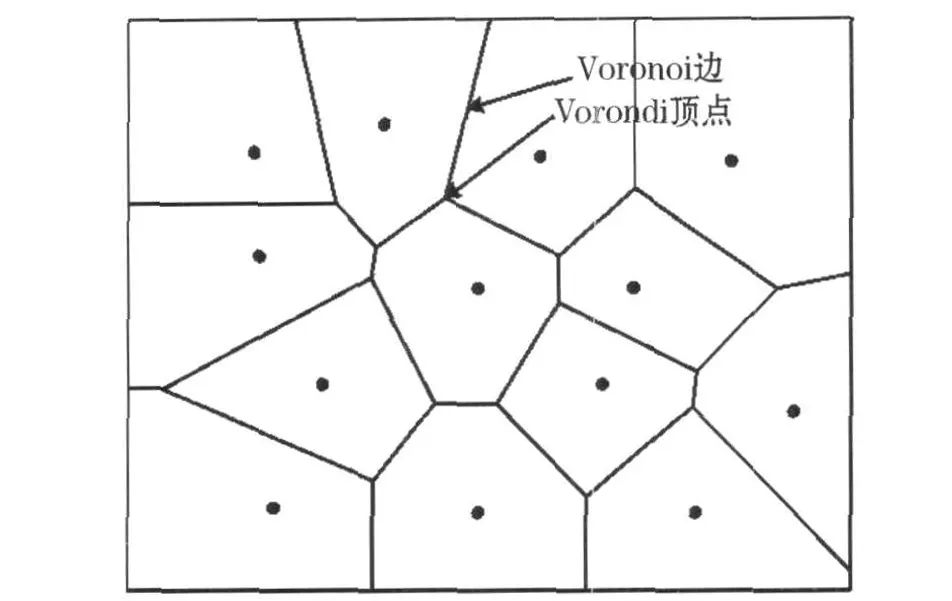
图1 Voronoi图

定义2:定义集合:N表示自然数集:N={1，2，3，…}，在本文N用来表示颜色数称为颜色集.Z表示整数集.R表示实数集，有N⊂Z⊂R.其它集合用普通的集合符号表示.向量p的坐标为，这里单位线段表示为

定义3:定义空间:

度量空间(Dn，d)中，Dn为线性空间，距离函数d∶，满足下列条件.

1)d(p，q)≥0;

2)d(p，p)=0;

3)d(p，q)=d(q，p);

4)d(p，q)+d(q，r)≥d(p，r).

其中:p，q，r∈Dn.

欧式空间(Rn，d)，距离函数为d∶

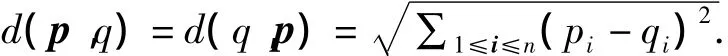
单位覆盖空间(In，d)，距离函数为

定义4:在(Dn，d)空间中，V(P，κ)为Voronoi划分，其中可数点集P⊆{p(i)|p(i)∈Dn，i∈N}，颜色函数κ∶p→N，用κ(p)表示点p的颜色.

定义如下:

1)V(p)={s|∀q∈Pd≤d(s，q)，s∈Dn}

表示Dn的点集中生成点p的最近邻点;

3)Pk⊂P中k为颜色:

Pk={p|κ(p)=k，p∈P};

5)Vk的边界:

若P中没有颜色为k的点，则Vk是空集.

定义5:V内单位元的相邻图G(V)=(C，E)，C为顶点集，E为边界集

2 构建颜色分块划分

首先有限集P0中m个不同的点P0={p(1)，p(2)，…，p(m)}⊂In，在单位覆盖空间(In，d)中的颜色Voronoi划分V0(P0，κ0)，这里(i))=i，所以中每个点都有惟一的颜色.

然后构建Voronoi划分序列Vh(Ph，κh)，其中

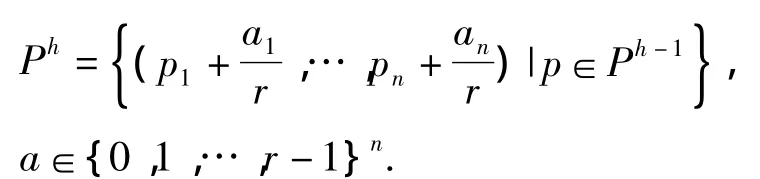
如果给出一些约束条件P0集，就能生成(I0，d)空间中覆盖在环面单位元连续的分块划分.这个简单的约束条件是G(V0)=G(V1)，这个条件将保证所有单位元是连续的.找到更困难的约束条件是保证至少有一个单位元是不连通集，见图2.

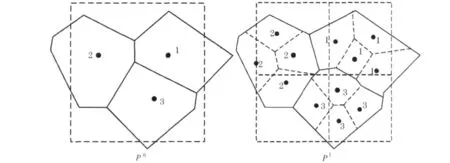
图2 在平面中以m=3为例，r=2，Voronoi划分图

3 生成算法

为了生成和形象化近似的分块划分T(n，r，m，P0)，我们用点替换规则，地图上用P0中的每个点替换P1中没覆盖的点集.同样的替换规则可以应用到Pk-1生成Pk.在Vk(Pk，κk)中的分块单元只要有足够大的k就能较好的接近分块划分V∞.

下面介绍一下∀p(i)∈P0的替换规则算法S(p(i))⊂Rn×N如下.

1)对∀p(i)∈P0，S(p(i))为空集;

2)对于∀a∈(0，1，…，r-1}n和p(i)∈P0有:

②满足∀s∈P0d(q，t)≤d(q，s)，κ(t)≤κ(s)利用距离函数d找到q的最近邻点t∈P0;

③计算出q和t之间的差:

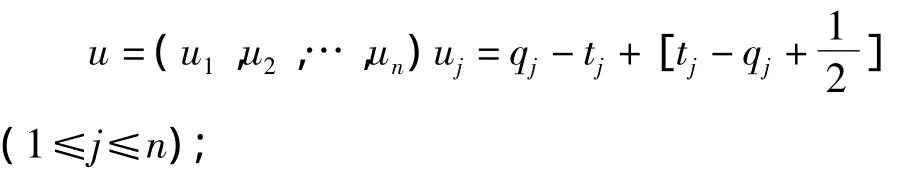
④(u，i)加入S(t).

生成Vk(Pk，κk)的算法，间隙为r规定指数c为p(c)∈P0的颜色.

1)Pk为空集;

2)对于∀p(c)∈P0:称为

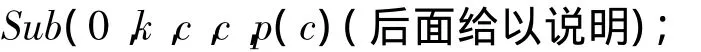
3)在Rn中计算几何的Voronoi图为Pk.提取Vk(Pk，κk)分块单位元的表面作为位于Voronoi单位元之间的用不同的颜色的表面.

程序Sub(i=iteration level，k=max.iteration，

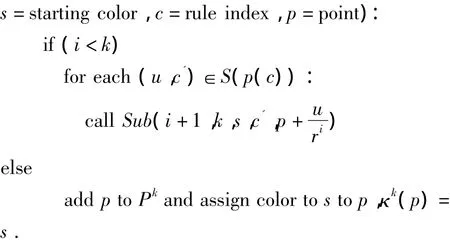
4 算法复杂度分析

该算法仅提取Vk分块单位元的表面还不是最理想的算法.由于Pk集是P0的周期，所以Pk的Voronoi图只包含m个不同的单位元图.因此我们可以计算Voronoi图V0和计算每次迭代后替换的周期分块.最好的方法是在迭代替换和计算最后的分块单位元时，要忽略所有的Voronoi单位元和用相同颜色包围Voronoi单位元的生成点.最理想的算法要求计算的次数与分块单位元表面的输出数成正比(或者Voronoi单位元的数量为不同颜色的相邻单位元).