随机利率下的再保险与投资策略研究

马 威，顾孟迪

(上海交通大学安泰经济与管理学院，上海200052)

比例再保险是当保险公司面临较大甚至是巨灾风险时进行风险转移的一项必要措施，它是原保险人将其承担的保险业务其中一部分转移给再保险人的行为.在比例再保险中最为关键的问题就是最优再保险，即考虑以何种形式分保以及安排具体分保的额度.而保险资金的有效投资是保险公司管理的重要内容之一.再保险与投资决策问题，是目前学术界关心的热点课题.

随机控制理论在再保险与投资问题的研究中得到广泛应用.Merton(1971)[1]利用随机控制方法讨论了连续时间最优投资组合问题，Browne(1995)[2]在公司保险盈余中引进标准布朗运动研究了具有随机风险公司的最大化生存概率.黎锁平和刘坤会(2003)[3]年将随机控制理论运用于证券投资问题，得出相应的最优控制策略.近来，有不少学者应用Hamilton–Jacobi–Bellman(HJB)方程研究最优再保险与投资策略，例如，Cao和Wan(2009)[4]考虑了服从标准布朗运动的股价，而Gu等(2010)[5]研究了股价服从常弹性方程过程时的最优策略.

随着国际金融环境的日趋复杂，利率的变性，在短期表现出随机性[6].现有再保险与投资策略的研究工作中都没有考虑利率的这种随机性，本文引进随机利率，使之更适合现实投资环境.

1 保险盈余过程

设索赔过程服从如下动态方程[7-8]:

其中:α，σ0为常量，分别表示为单位时间平均索赔额和索赔波动率，w(0)t为标准布朗运动.

设保费为:q=(1+φ)α，φ＞0为保险安全负荷，即q＞α.这意味着公司实际收取的保费应该能够补偿向投保人支付的索赔额以及各项附加费用.

在既无再保险，也未作投资时，保险公司的盈余过程为:

在比例再保险中，再保险人在接受保险公司一定的报酬的情况承担一部分赔偿责任.设再保险比例为(1-a)，即每份保额由保险人承担100a%，剩余100(1-a)%由再保险人承担.在保期末，保险人向再保险人以费率λ(1-a)支付再保险费，其中，λ≥φα，保险公司的盈余过程为:

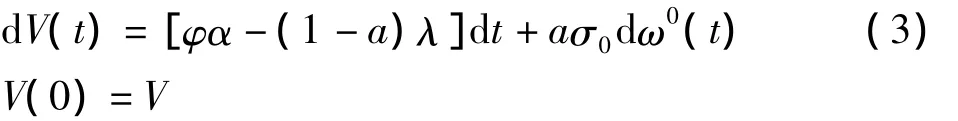
以S表示风险资产的价格，设其服从Black-Scholes过程:

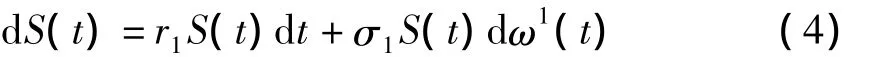
其中:r1，σ1＞0为常量，分别表示风险资产的期望回报率与波动率，ω1(t)为独立于ω0(t)的标准布朗运动.

以B表示无风险资产价值，并引入Hull-White随机利率模型，则有:

其中:l，θ及σr都为t的确定性函数.l决定了利率的长期平均水平，θ是调整短期和长期利率关系的平均回复率，ω2(t)为与ω0(t)和ω1(t)相关的标准布朗运动.

又因为ω1(t)独立于ω0(t)我们可设ω2(t)与ω0(t)的相关系数为 ρ1，ω2(t)与 ω1(t)的相关系数为 ρ2，且

以b代表保险盈余投资于风险资产的部分，保险公司的盈余可以表示为:

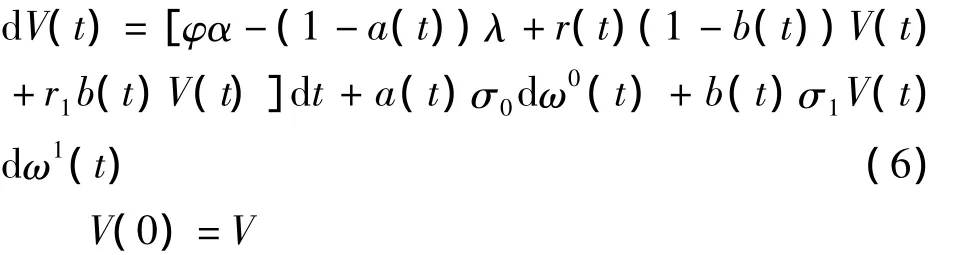
显然，自担风险比例a与风险资产投资比例b构成了保险人的策略.动态过程(a(t)，b(t))称为策略εt.

2 HJB方程及其求解

在上述模型的基础上，为寻求最优投资策略，我们以财富期望效用最大化为目标，即求解

设保险人追求期末财富效用最大化，而其效用函数是常绝对风险规避(CARA)的:

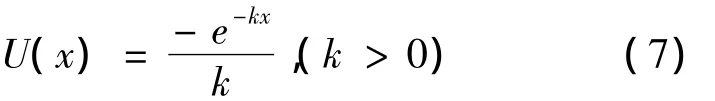
对策略εt，定义在时间t，保险人从财富状态v时得到的效用为:

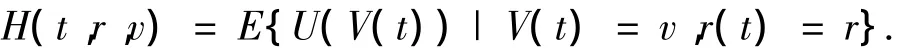
目标是求解最优价值函数:

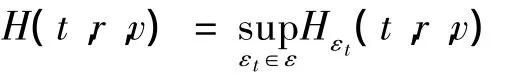
该问题的HJB方程为:

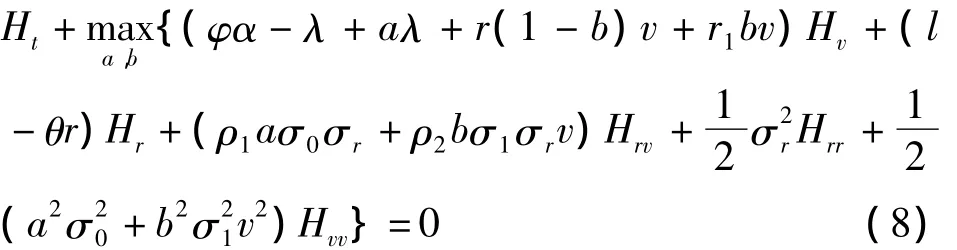
由一阶条件可得:

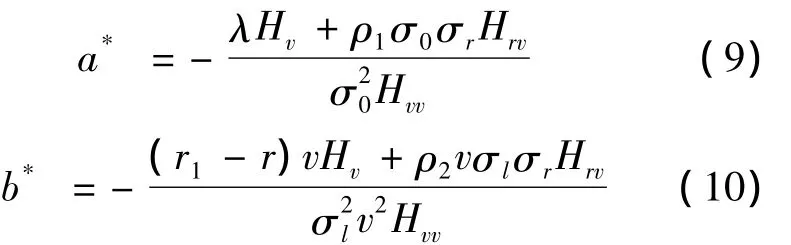
考虑CARA效用函数(7)下我们可设H其为如下形式:

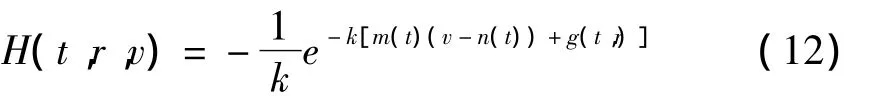
其中:m(T)=1，n(T)=0，g(T，r)=0

故有:

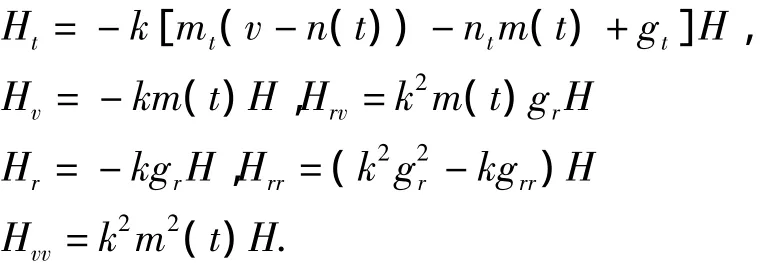
代入式(11)并整理可得:

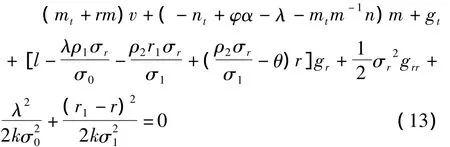
由式(13)可得如下方程组:

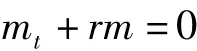
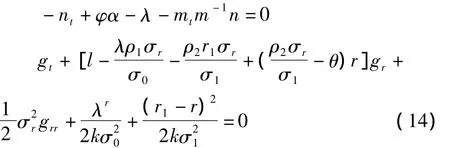
结合m(T)=1，n(T)=0可解得:

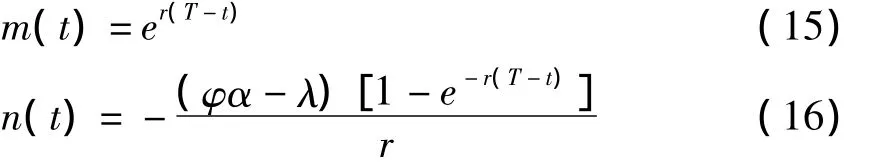
为求解方程组(14)中第三个方程，我们设:

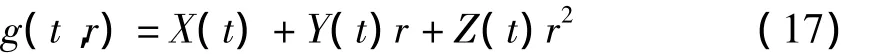
其中:X(T)=0，Y(T)=0，Z(T)=0

代入式(14)中第三个方程得

令:

整理(18)得:

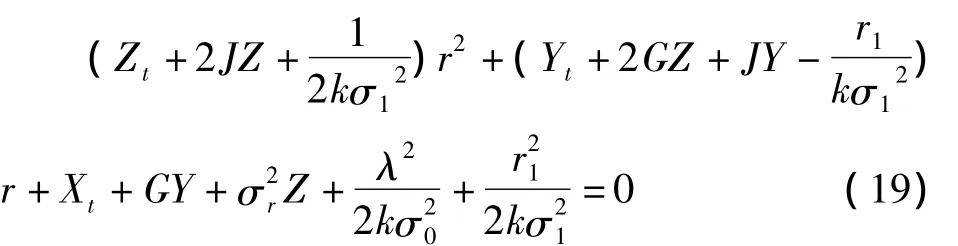
由式(19)可得如下方程组:

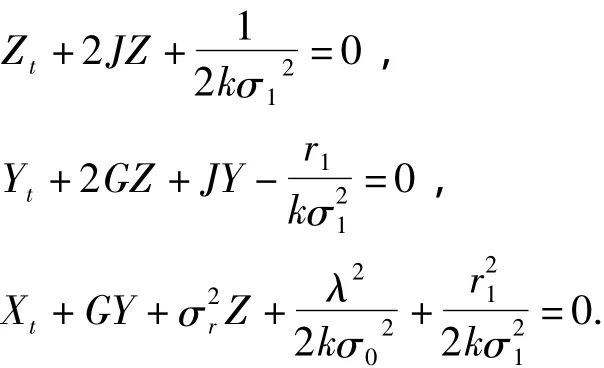
结合X(T)=0，Y(T)=0，Z(T)=0解之可得:

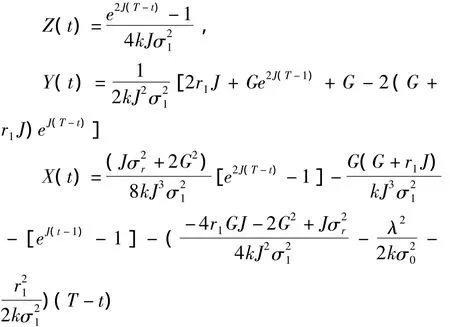
因此，最优最保险与投资策略为:

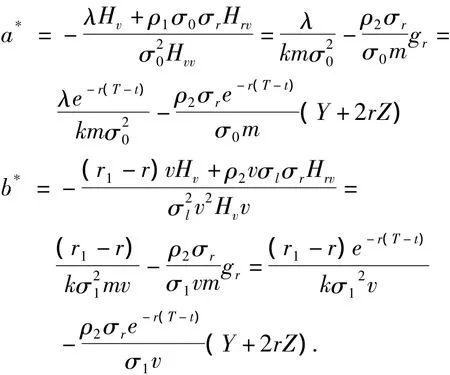
其中:

3 结语

保险公司的最优再保险与投资决策是近年来学术界关注的一个问题，但现有研究中都没有考虑利率的随机性.本文在考虑随机利率的情况下建立了公司保险盈余模型，在CARA效用函数下利用HJB方程求得了最优解，给出了保险公司的最优再保险比例及投资比例.由于这类问题的复杂性，能够求解出解析解的情况不多，而考虑随机利率更加大了问题的复杂程度.本文得到了CARA效用下的解，但CRRA效用下仍然无法求解.今后可以尝试用数值方法来分析这些问题.

[1]MERTON R C.Optimum consumption and portfolio rules in a continuous times model[J].Journal of Economics Theory，1971，3:373-413.

[2]BROWNE S.Optimal investment policies for a firm with a random risk process exponential utility and minimizing the probability of ruin[J].Mathematics of Operations Research 1995，20(4):937-958.

[3]黎锁平，刘坤会.随机控制的HJB方程与证券投资模型[J].北方交通大学学报，2003，27(6):63-67

[4]CAO Y，WAN N.Optimal proportional reinsurance and investment based on Hamilton-Jacobi-Bellman equation[J].Insurance:Mathematics and Economics2009，45，157-162.

[5]GU M，YANG Y，LI S，et al.Constant elasticity of variance model for proportional reinsurance and investment strategies[J].Insurance:Mathematics and Economics，2010，46，580-587.

[6]刘 坚，杨向群，颜李朝.随机利率和随机寿命下的欧式未定权益定价[J].广西师范大学学报，2005，23(4):49-52

[7]PROMISLOW D S，YOUNG V R.Minimizing the probability of ruin when claims follow Brownian motion with drift[J].North American Actuarial Journal，2005，9(3):109-128.

[8]罗 琰，杨招军.保险公司最优投资及再保险策略[J].财经理论与实践，2009，30(159):31-34.