分离变量法在静电场问题中的应用

张保花 郭福强 李艳青

(1,2,3.昌吉学院物理系 新疆 昌吉 831100)

1 引言

静电场问题是电动力学的核心问题[1]，是继电磁学理论之后的重要理论知识。利用电磁学所学知识对一些实际问题不能解决，而电动力学是在人类对电磁现象的长期观察和生产活动中发展起来的，对解决实际问题起到了十分重要的作用。本论文就是把电磁场的基本理论应用到实际情况，其研究的主要问题是：在给定的自由电荷分布以及周围空间中存在介质或导体分布的情况下，怎样求解静电场问题，主要介绍利用分离变量法求解静电场的一般步骤，并在不同的环境下分离变量法对边界条件和边值关系的适当选择。

2 分离变量法求解的方程及通解

▽2φ=0

(1)

上式称为拉普拉斯方程(拉氏方程)。产生电场的电荷都分布于区域V的边界上，它们的作用通过边界条件反应出来。因此，这类问题的解法是求拉普拉斯方程的满足边界条件的解，(1)式的通解可以用分离变量法给出。

先根据界面形状选择适当的坐标系，然后在该坐标系中用分离变量法解拉普拉斯方程。最常用的坐标系有球坐标系和柱坐标系[3]。这里写出用球坐标系中轴对称情形下拉普拉斯方程的通解形式。

在球坐标系下，球坐标用(R,θ,φ) 表示，R为半径，θ为极角，φ为方位角，则拉氏方程在球坐标系中的通解为：

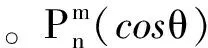
(3)

Pn(cosθ)为勒让德函数，an和bn是任意常数，由边界条件或边值关系确定。所以，在每一个没有电荷分布的区域内，φ满足拉普拉斯方程，其通解已有(2)或(3)式给出，剩下的问题就是由具体的边界条件或边值关系确定这些通解中所含的任意常数，从而得到满足边界条件下的特解。

3 分离变量法的一般解题步骤

从分离变量法求解的方程及通解中，可以总结出分离变量法的一般解题步骤：

首先，当所求区域中的电荷密度ρ=0时，自由电荷只分布在某些介质或导体表面上，将这些表面视为区域边界，并且电势φ满足 ▽2φ=0，则可以用分离变量法求解拉普拉斯方程；

其次，对实际情况分析，满足球对称或轴对称，写出相应的拉普拉斯方程通解；

再次，从实际情况出发，依次找出边界条件和边值关系来确定通解中的待定系数。

概括起来，大致有以下几种类型的边界条件[4]：

(1) 两种绝缘介质界面上，边值关系为

φ1=φ2

应用这条件可以把界面两边的电势衔接起来。

(2)给出导体上的电势，导体面上边界条件为

φ=φ0(给定常数)

(3)给出导体所带总电荷Q，在导体面上的边界条件为

φ=常数 (待定)

应用上述边界条件可以唯一地解出静电场，用导体面上的另一边界条件

可以得出导体面上的自由电荷面密度σ。

对于介质和导体存在的边值关系：

(1)两介质交接面上边值关系

(2)导体表面上的边值关系

由于导体表面为等势面，因此在导体表面上电势为常数。将介质情况下的边值关系用到介质与导体的分界面上，并考虑导体内部电场为零，则可以得到第二个边值关系：

4 分离变量法的实际应用

介质球的存在使空间分为两均匀区域—球外区域和球内区域。两区域内部都没有自由电荷，因此电势都满足拉普拉斯方程。以φ1代表球外区域的电势，φ2代表球内区域的电势。由(3)式，两区域的通解均为：

(4)

(5)

an,bn，cn和dn是待定常数。

边界条件包括：

φ1→-E0Rcosθ=-E0RP1(cosθ)

(6)

因而 (a1=-E0,an=0(n≠1)

(7)

(2)R=0处， φ2应为有限值，因此 dn=0 ；

(8)

把 (4)和(5)式代入(8)式得

(9)

(10)

比较(9)式其它Pn项的系数可解出 bn=cn=0,n≠1 (12)

所有常数已经定出，因此本问题的解为

(13)

总之，通过以上例题求解了静电场，使学生们更容易掌握在求解静电场问题时分离变量法的解题步骤，以及在不同情况下静电场所满足的边值关系及边界条件[6]，学生们比较轻松的学习了静电场的求解问题，记忆更加深刻，能够更准确、更熟练地应用于解决实际问题。

参考文献：

[1]郭硕鸿.电动力学(第三版)[M].高等教育出版社，2008.

[2]郭劲.镜像法在静电场和静磁场的比较[J].高教研究，2000，(3)：31-33.

[3]尹真.电动力学(第二版)[M].科学出版社，2006.

[4]陈世民.电动力学简明教程[M].高等教育出版社，2004.

[5]郑春开.电动力学解题指导[M].北京大学出版社，2004.

[6]俞允强.电动力学简明教程[M].北京大学出版社2003.