基于参数灵敏度分析的吊杆索力识别

陈彦江，程建旗，闫维明，何浩祥，李 勇

(北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

吊杆是钢管混凝土系杆拱桥重要的受力构件，吊杆索力的精确测量不仅是整座桥梁施工监控的重要环节，而且也是后期桥梁养护管理与健康监测最关心的问题。由于振动法测索力有其很多优势而被广泛应用［1]。

目前，应用各种加速度传感器及频谱分析技术，可以较精确得到吊杆的基频或前几阶固有频率［2]。因此利用振动法测索力的精度主要取决于计算式的选取。从吊杆受力模型简化角度分，目前存在的振动法测索力方法主要有以下三类:

第一类方法是基于拉紧的弦振动理论的公式，忽略吊杆的抗弯刚度，并视吊杆两端为铰接［3，4]:

式中，f1为吊杆的基频;T，m，l分别是吊杆索力、单位长度质量和计算长度。

第二类方法考虑了吊杆的抗弯刚度，将吊杆视为两端简支轴向受拉梁［5]:

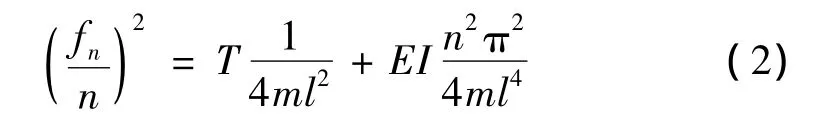
式中，fn为吊杆的第n阶固有频率;EI为吊杆的抗弯刚度。

第三类方法考虑吊杆的抗弯刚度和两端固结边界条件，推导出了含索力、频率的超越方程，并在此基础上，应用能量法迭代计算出经验拟合公式［6]。然而，上述的三类方法都存在着不同程度的缺陷:

(1)第一种方法忽略了吊杆抗弯刚度的影响。对于长度较小的吊杆，抗弯刚度对吊杆频率影响很大，用式(1)计算将得到偏大索力值。

(2)第二、三种方法虽然考虑了吊杆的抗弯刚度，但抗弯刚度的影响作为显式的计算参数。在工程实践中，吊杆内部结构形式、钢丝间的粘结程度、索力大小等不确定因素的影响，吊杆的抗弯刚度 EI难以准确识别。

(3)早期修建的钢管混凝土系杆拱桥，多数吊杆锚固时采用钢套管并内灌水泥砂浆护索，吊杆两端近似于固结［7]。近几年吊杆多采用带球形支座的锚具锚固，如图4。且钢套管内不再灌水泥砂浆，而是设置橡胶减震器，显然其两端约束情况用固结来模拟已不再适用，而且索的计算长度由于受减震器的影响，采用上下锚固点之间的距离也将产生很大的误差。

(4)对于短吊杆，环境激励下基频很难被激发，限制了上述公式中用基频计算索力的应用，使得短吊杆(＜5m)不能通过振动法来测出索力［8，9]。

针对上述计算方法中存在的缺陷，本文提出基于吊杆参数灵敏度的优化算法计算索力值。该方法假设吊杆两端铰接并考虑抗弯刚度影响，以索力、抗弯刚度和计算长度作为未知参数，通过计算长度修正来考虑实际吊杆边界条件简化为两端简支后引入的误差［10，11]。首先分析吊杆频率对各参数的灵敏度，然后基于参数灵敏度矩阵进行迭代计算。数值分析表明，这种算法不仅收敛速度快，且特别适用于固有频率受抗弯刚度影响较大的短吊杆。并通过对一座钢管混凝土拱桥的吊杆测试分析验证了该方法的可行性。

1 基于吊杆参数灵敏度的优化算法

考虑索的抗弯刚度，忽略剪切变形和转动惯量的影响，此时吊杆受力就相当于一轴向受拉梁，其运动微分方程为［12]:

假定解具有形式:

即幅值Y(t)随时间变化，Φ(x)是指定形状函数。

分离变量得:

其中:

对于任意轴向力，式(6)中的 D1、D2、D3、D44 个参数定义了索振动的形状。可由两端铰接边界条件得出:

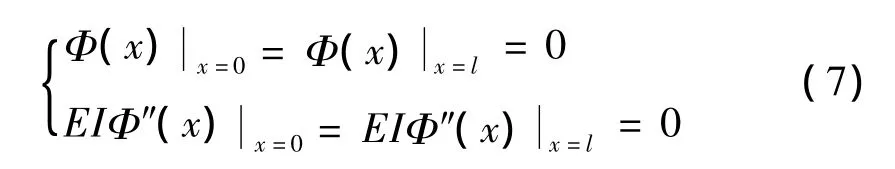
把上式代入式(6)，D1、D2、D3、D4不全为零，则由方程组行列式为0可计算出:

上式就是考虑轴向力和抗弯刚度影响的吊杆固有频率与索力的关系式。式中吊杆单位长度质量m在出厂时可精确测量，且在营运过程中变化量很小，作为已知量。将索力T、抗弯刚度EI和计算长度l作为未知参数，构成变量列阵P，即:

因此式(8)可记作fj=F(P)，其中fj是吊杆的第j阶固有频率(j=1，2…n)。

fj在设计变量P处按Taylor级数一阶展开得:

式中Pi是变量列阵P中第i个变量，这里P有3个元素，所以r=3，i=1，2，3。忽略高阶项的影响，则固有频率增量δfj为:

因为索力T，抗弯刚度EI，和计算长度l具有不同的量纲，且数值大小也相差几个数量级，仅从灵敏度表达式Sp还不能判断固有频率最敏感的参数，因此，式(11)可进一步写成:

将式(14)进一步简化为:

式中，U是n×1阶列向量，表示各阶频率相对变化量;ε是r×1阶列向量，表示参数变量的相对变化量;ε是n×r阶矩阵，表示参数变量的差分相对灵敏度。具体形式如下:

应用迭代法求解方程(15)可分以下6个步骤:

(1)置迭代步 k=0，设定设计变量 P的初始值P0= ［T0EI0l0]T;

(3)计算频率的相对变化量Uk，可采用下式:

(5)计算参数的相对变化量:

(6)修正吊杆的参数变量，得到第k+1次迭代时参数估计值:

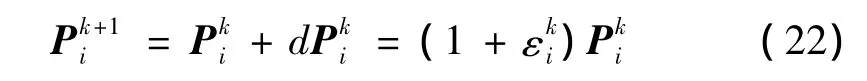
重复以上的迭代过程，直到列向量U收敛到0，迭代结束，此时的设计变量P即为吊杆参数精确值。

上述迭代算法实质是非线性优化问题，考虑各参数变量的实际物理意义，并加快迭代收敛速度，引入各参数的约束条件，如下:

索力值T的上、下限可根据设计索力值设定一个较大的初始区间;计算长度l的下限L0为最外侧减震器间的间距，上限L为锚垫板间的间距，如图4;对于抗弯刚度，文献［8]用单根钢丝的抗弯刚度之和作为整个吊杆的抗弯抗度，文献［9]则用同等直径的钢柱作为吊杆的抗弯刚度。而事实上，吊杆的抗弯刚度介于上述最小值和最大值之间。因此，EImin为单根钢丝的抗弯刚度值之和，EImax为同等直径钢柱的抗弯刚度。

2 数值分析

将第1节算法编成Mat lab程序，选取文献［9]中4根吊杆，来验证该算法的可行性，各吊杆的参数如表1所示。

表1 各吊杆参数值Tab.1 Parameters of hanger rods

吊杆1长度＜5 m，且ξ值很小，表示固有频率受抗弯刚度影响较大［15];吊杆2、3虽然索力和抗弯刚度值不同，但ξ值近似相等，属于受力性能相近的吊杆;吊杆4代表长吊杆，索力值和计算长度都较大，ξ值也比较大。

分析上述4根吊杆前20阶固有频率分别对索力、抗弯刚度和计算长度的灵敏度，分析结果如图1、图2、图3所示。

从下面3个图可以看出:

(1)频率对索力的相对灵敏度随着阶次的增加而减小，频率对抗弯刚度、索长的相对灵敏度随着阶次的增加而变大，且频率对索长的相对灵敏度是负值;

(2)相对于索力和抗弯刚度两参数，索的各阶频率对索长的相对灵敏度最大。低阶频率时，频率对索力的相对灵敏度大于对抗弯刚度的相对灵敏度，高阶频率时，频率对抗弯刚度的相对灵敏度大于对索力的相对灵敏度;

(3)2号、3号吊杆因为ξ值近似相等，各参数的相对灵敏度也基本相等。1号吊杆ξ值比4号吊杆ξ值小，因此频率值对抗弯刚度的相对灵敏度1号吊杆比4号吊杆大，频率值对索力的相对灵敏度1号吊杆比4号吊杆小。

图1 各阶频率对索力的相对灵敏度Fig.1 Relative sensitivity to tension force

图2 各阶频率对抗弯刚度相对灵敏度Fig.2 Relative sensitivity to flexural rigidity

图3 各阶频率对索长相对灵敏度Fig.3 Relative sensitivity to length

分别计算上述4根吊杆的前4阶固有频率，并假设为实际测量真实值，吊杆的索力、抗弯刚度和计算索长作为未知参数，通过第1节中所述迭代算法计算各吊杆索力值T，抗弯刚度EI和计算长度L。

为了验证算法对不同的初始值都收敛到精确解，迭代步骤(1)中初始值T0、EI0、L0取不同值:1号吊杆分别取真实值的80%，80%，80%;2号吊杆分别取真实值的120%，120%，120%;3号吊杆分别取真实值的80%，150%，60%;4号吊杆分别取真实值的130%，70%，150%。计算结果如表2所示，表中最后一列是式(1)在已知计算索长，不考虑抗弯刚度时由基频计算的索力值。

从表中计算结果可以看出:

(1)基于拉紧的弦振动理论的公式在吊杆ξ值较小时，计算索力值将引起很大误差，且是偏大值。如表中吊杆1的计算索力值相对误差为10.5%，若用高阶频率计算时，误差将更大，因为高阶频率受抗弯刚度影响更大;

(2)采用本文介绍的迭代算法时，各参数的误差基本都在5%以内。其中，计算索长精度最好，主要原因是各阶频率对索长都较敏感，更容易收敛于真实值，而2号、3号、4号吊杆的抗弯刚度值的计算结果误差较大，是由于这3根吊杆ξ值较大，各阶频率对抗弯刚度相对不敏感，迭代时收敛速度较慢，误差也较大。

(3)2号、3号吊杆虽然长度不等，但是力学性能基本相同。因此，长、短吊杆的分类不能简单的只依赖于索的计算长度的大小。用ηn表示考虑和不考虑抗弯刚度时吊杆的第n阶频率的比值，由式(1)、式(8)可得:

表2 吊杆各参数计算结果Tab.2 Estimation results of the parameters

3 工程应用

102国道跨伊通河大桥是三跨飞燕式异性钢管混凝土拱桥，主跨158 m，桥宽40 m。主拱共设16对吊杆，顺桥向间距6 m，规格均为LZM7－61型，索体采用PES(FD)系列新型低应力防腐拉索。如图4，每套吊杆包含吊杆两端锚头、螺母、减震器、和保护罩。吊杆长度L是指每根吊杆两端锚头锚垫板之间的理论长度值，L0是最外侧减震器间距离。

在施工调索期间，选取其中3根吊杆进行监测，各吊杆的参数见表3。将A104型无线加速度传感器固定在吊杆上，以200 Hz采样频率进行采样。后将时程序列重采样并低通滤波将高频部分滤掉，且去除趋势项后，得到各吊杆的频谱图。吊杆B加速度时程曲线和频谱图分别如图5、图6所示。

从图6中明显识别出吊杆前6阶频率分别为5.792 Hz，11.665 Hz，17.698 Hz，23.896 Hz，30.241 Hz，36.278 Hz。

应用第1节中所述迭代算法，A、B、C 3根吊杆各参数的上、下限如表3中所示，计算结果见表4，表中式(1)的计算长度选取本文的计算结果，即表中第4列。将各计算值与同步张拉吊杆的千斤顶油压表读数相比较，本文方法的计算索力值误差较小，能满足工程精度要求。

图4 吊杆锚固详图Fig.4 Structure of hanger rod

图5 吊杆B加速度时程曲线Fig.5 Acceleration time-history responses of rod B

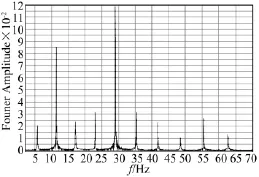
图6 吊杆B频谱图Fig.6 Power spectrum density of rod B

表3 吊杆拉索参数表Tab.3 Parameters of hanger rods

表4 吊杆各参数计算结果Tab.4 Estimation results of the parameters

4 结论

本文分析了吊杆频率对索力、抗弯刚度和计算长度3参数的灵敏度，同时提出了基于灵敏度分析的优化算法，可同时计算出3参数。该方法有三点优势:

(1)计算精度高，考虑了抗弯刚度对各阶频率的影响，特别适用于ξ值≤20的短吊杆;

(2)不引入考虑吊杆未知边界条件的参数，而是用计算长度来修正吊杆两端等效成简支约束后的影响;

(3)不仅能计算出索力值，而且还能较精确得到吊杆的抗弯刚度。此方法用于振动法监测吊杆，不需要建立和修正吊杆的有限元模型，可实时用计算索力值和抗弯刚度双参数对吊杆和整个桥梁结构进行健康状态评估。

［1] 侯立群，欧进萍，赵雪峰，等.哈尔滨四方台斜拉桥模态参数和索力识别［J] .振动与冲击，2009，28(5):106－110.

［2] Kim B H，Stubbs N，Park T.A new method to extract modal parameters using output-only responses［J] .Journal of Sound and Vibration，2005，282(1):215－230.

［3] Zui H，Shinke T.Practical formulas for estimation of cables tension by vibration method［J] .Journal of Structural Engineering，1996，11(6):651－656.

［4] Riceiardi G，Saitta F.A continuous analysis model for cables with sag and bending stiffness［J] .Engineering Structures，2008，2(30):1459－1472.

［5] Marcelo A C，Carlos A P.Determination of axial force on stay cables accounting for their bending stiffness and rotational end restraints by free vibration tests［J] .Journal of Sound and Vibration，2008，317(10):127 －141.

［6] 任伟新，陈 刚.由基频计算拉索拉力实用公式［J] .土木工程学报，2005，38(11):26－31.

［7] Kim B H，Park T.Estimation cable tension force using the frequency-based system identification method［J] .Journal of Sound and Vibration，2007，304(3):660－676.

［8] 孟少平，杨 睿，王景全.一类精确考虑抗弯刚度影响的系杆拱桥索力测量新公式［J] .公路交通科技，2008，25(6):87－91.

［9] 朱卫国，申永刚，项怡强，等.梁拱组合体系桥柔性吊杆索力测试［J] .中南公路工程，2004，29(1):21－23.

［10] 刘文峰，应怀樵，柳春图.考虑刚度及边界条件的索力精确求解［J] .振动与冲击，2003，22(4):12－l4.

［11] 张宇鑫，李国强，赵世峰.张弦梁结构振动方法索力识别(Ⅰ):振动特性的参数分析［J] .振动与冲击，2009，28(3):152－157.

［12] Ray W C，Joseph Penzien.Dynamics of structures［M] .Computers and Structures，Inc.2003.

［13] Hua X G，Ni Y Q，Chen Z Q，et al.Structural damage detection of cable-stayed bridge using changes in cable forces and model updating［J] .Journal of Structural Engineering，2009，135(9):1093－1106.

［14] Irvine H M. Cable structures［M] . The MIT Press，Cambridge，1981.

［15] 段 欣，刘伟庆.拉索的特征灵敏度分析［J] .贵州大学学报，2009，26(4):134－136.