阈值协整中内生性解释变量下参数推断的比较

刘汉中

(湖南商学院 经济与贸易学院，长沙 410205）

0 引言

目前，协整分析方法已经成为宏观经济或金融经济学中的重要工具之一，在大多数的协整分析中，主要集中在协整关系的检验和协整参数的估计两个方面，而对协整参数向量的推断或长期关系检验(也常称为参数的约束性检验)往往被忽视。实际上，对于协整参数的推断有时候是十分必要的，如在购买力平价理论的检验中，只有协整参数满足一定的数量关系时购买力平价理论才成立，这样必须对协整参数进行约束性检验，只有当约束性条件成立时购买力平价理论才成立；在生产函数研究中，协整参数的推断可以帮助我们判断规模报酬是递增、递减或不变，如果参数之和大于1则认为是规模报酬递增的，这时同样要对协整参数是否满足约束性条件进行检验。

阈值协整(Threshold Cointegration)是由Balke和Fomby(1997)[1]提出来的，从目前的文献来看，阈值协整参数估计仍然是采用OLS法，因为OLS估计在阈值协整参数估计中仍然满足超一致性。但是，根据Balke和Fomby(1997)的阈值协整定义[2]，参数的OLS估计量所构造的检验统计量必然呈现不同的性质，因为在阈值协整方程式中，随机干扰项本身蕴含有非线性的自相关结构，常规的OLS估计程序通常会低估统计量的标准误(Standard Error)，从而使得t统计量被高估，增大拒绝原假设的概率。同时由OLS估计量构造的F或Wald统计量也会被高估，从而引起协整参数推断的误导。另外如果在阈值协整中，解释变量具有内生性时，同样的问题是OLS估计量构造的t、F或Wald统计量不再具有标准的极限分布，其极限分布也依赖于冗余参数，常规的t、F或Wald检验已经失去意义，因此对阈值协整参数的修正估计并由此构造参数约束性检验统计量就显得十分必要。本文拟这一研究背景下，利用三种修正的估计法来构造相应的检验统计量，展开对阈值协整参数的推断，目的在于揭示三种修正方法在阈值协整参数推断中适用性。具体而言，在有限样本下，我们将通过对各种阈值协整设定下的三种估计法(FM-OLS、CCR和DOLS)所构造的检验统计量进行模拟并与标准正态分布进行比较，找出各统计量的经验分布和标准正态之间的差距，找出影响各推断方法与阈值协整参数设定和样本容量变化的变化规律，揭示各种方法在阈值协整参数推断中的适用性，从而提供适用于阈值协整参数推断的估计方法。

1 阈值协整概述

其中Xt、Yt都是I(1)过程，μt是I(0)过程，且可以表示为一个平稳的自回归过程。如果(1)式中的协整误差项μt的数据生成过程(DGP)是以下阈值自回归模型(TAR)：

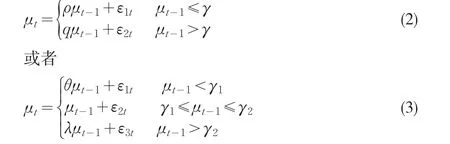
根据Balke和Fomby(1997)的定义，有如下的模型：

其中：参数β是变量之间的阈值协整系数向量，γ是阈值变量，μt-1是转换变量，则这时的协整被称之为阈值协整。如果协整误差项是形如式(2)的数据生成机制，则称为两机制的阈值协整；如果是形如式(3)的数据生成机制，则称为三机制的阈值协整。阈值协整的误差修正模型具有非线性调整机制，从而对变量短期变化产生不同的调节效应，所以阈值协整对应的ECM是长期均衡和短期波动的非线性阶梯函数，这种非线性调节对于检验经济学和金融学理论具有重要的意义(刘汉中，2007)。

如果上面的式(1)表示阈值协整时，随机干扰项必须服从形如式(2)和(3)所示的TAR模型，且同时也要满足平稳性。对于TAR模型的平稳性，Chan和Petruccelli等(1985)[3]提出了式(2)满足平稳遍历的充分条件，即；ρ×q＜1,ρ,q＜1 Bec、Salem和Carrasco(2004)[4]提出了式(3)的平稳遍历性条件，即θ×λ＜1,θ,λ＜1，且不论中间机制数据过程是否为单位根过程。

2 阈值协整参数估计法以及相应估计量的极限分布

2.1 FM-OLS估计及其估计量极限分布

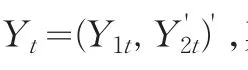
其中随机干扰项μ1t是形如式(2)或(3)所示的TAR模型，协整系统的随机干扰项向量μ'=(μ'1,μ'2)'，协整向量表示为β'=(α,γ')'，μ的长期方差-协方差分块矩阵可以表示为：

在（5）式中如果矩阵 Σ21不为0，说明阈值协整方程的随机干扰项与解释变量是相关的，即Y2t不满足严格外生性，则阈值协整系数的OLS估计不再具有渐近的正态分布。

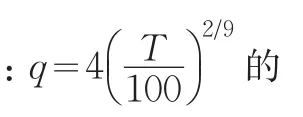
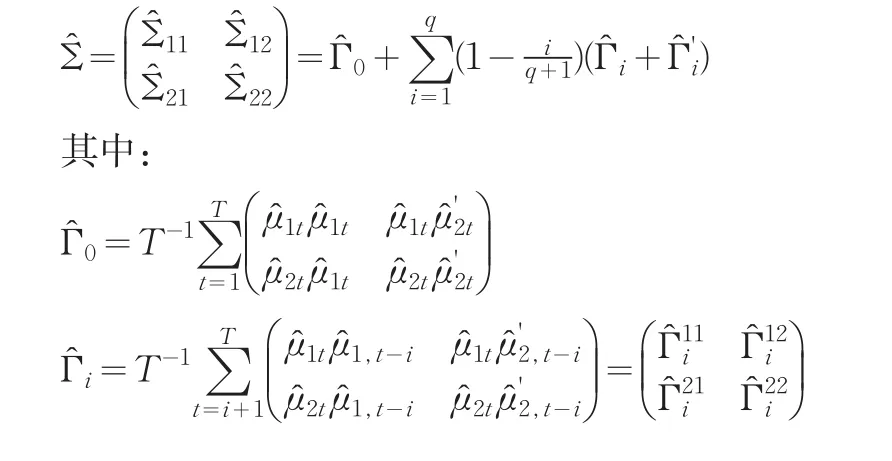
1t,2t分别表示协整系统的OLS估计残差或残差向量。将式(4)的阈值协整方程两边同时减去项得到：

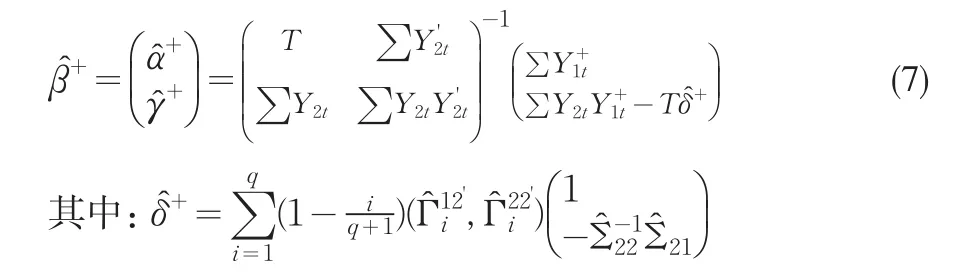
根据Phillips和Hansen(1990)，我们很容易证明参数的FM-OLS估计量具有以下的极限分布：

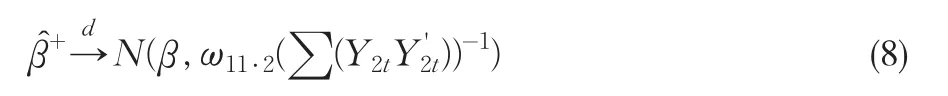
其中是阈值协整模型在FM-OLS估计量下的随机干扰项的长期方差。因此阈值协整参数的FM-OLS估计量的极限分布为正态的，由此所构造的t统计量具有标准正态的极限分布，且对参数的约束性检验所构造的Wald统计量具有标准的极限分布。

2.2 正则协整回归(CCR)法以及相应的极限分布

基于(4)所示的三角形表述，长期的方差-协方差矩阵可以分解为：矩阵可以表示为则CCR方法的数据过程变换如下：

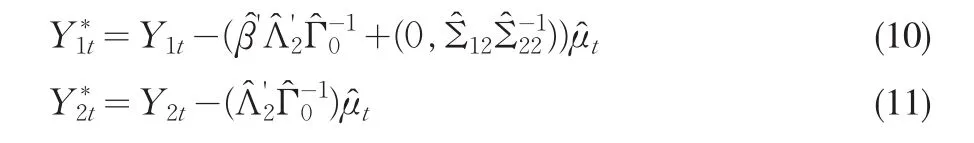
对(12)进行OLS估计就是阈值协整参数的CCR估计量，同时在(12)式中已经消除了内生性。根据Park(1992)，我们很容易得到阈值协整参数的CCR估计量具有FM-OLS估计量相同的极限分布，其中ω11⋅2是(12)式的随机误差项的长期方差。同样基于该估计量构造的Wald统计量具有渐近的χ2分布，构造的t统计量具有渐近的标准正态分布。

2.3 动态OLS估计(DOLS)

与非参数的FM-OLS和CCR方法不同，DOLS是基于协整回归式，加入解释变量的一阶差分项的超前(Leads)与滞后(Lags)作为回归方程的解释变量，这样可以消除解释变量的内生性，然后再针对新的回归模型进行OLS估计，以此求得阈值协整参数的估计量。用公式表示如下：

通过对上式进行OLS回归，求得参数α、γ的OLS估计量就是阈值协整参数的DOLS估计量，并且根据Stock和Watson(1993)和Hayashi(2000)，可以得到：

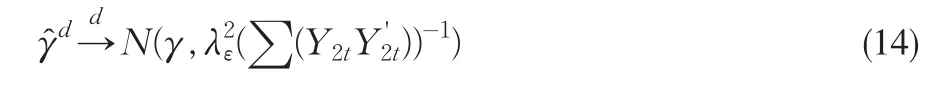
其中表示阈值协整参数向量的DOLS估计，要特别注意的是向量不包括α和πi参数的估计量，即(14)式只对长期协整参数是成立的，而对截距和差分项前面的参数是不成立的。另外表示模型(13)中的随机干扰项εt的长期方差。由此可见，DOLS估计量所构造的t统计量和Wald统计量具有渐近的标准分布，即分别趋于标准正态分布与标准的χ2分布，这样可以利用标准分布对阈值协整回归参数进行统计推断。

从上述分析看，三种修正估计量具有相同的极限分布，其方差-协方差矩阵都包含有随机误差项的未知的长期方差参数，因此必须要对其进行估计。本文以DOLS法下的长期方差估计为例，由于(13)的设定并不能保证随机误差项εt不存在自相关，因此长期方差的估计可以采用以下方法来估计：①拟合残差εt的AR(L)自回归模型；②计算是随机干扰项的方差估计，Den Haan和Levin(1996)[7]认为该估计量是残差长期方差的一致估计量，滞后阶L可以通过赤池信息准则(AIC)或贝叶斯准则(BIC)来确定。另外对于(14)式的滞后阶K的确定：运用AIC、许瓦兹信息准则(SC)或利用一般到特殊的建模步骤来确定最佳阶数(Ng和Perron，1995)[8]。

这三种协整参数的修正估计法都是通过适当的变换，消除解释变量的内生性，从而使得估计量具有标准的极限分布，避免了由于协整变量的内生性而导致的参数OLS估计量的非标准分布问题，因此极大地方便了协整参数的推断，同时也减少了OLS估计量的小样本偏差。另外刘汉中(2010)[9]已经证实三种修正方法都能修正阈值协整参数OLS估计的小样本偏差，但是通过三种估计法来对阈值协整参数的约束性检验进行推断，目前的研究还很少，因此本文正是出于这一目的，将对三种估计量在参数约束性检验中的适用性进行研究，尤其是阈值协整变量是内生性变量时，协整参数的约束性检验进行研究，在此基础上提出最适宜的修正估计法。3Monte-Carlo模拟设计及其结果

利用三角形表述设定以下的阈值协整系统，为了简单起见也不影响一般性，Y1和Y2设定为一维的I(1)单位根过程：

其中μ1t服从TAR(1)模型，说明Y1和Y2之间存在阈值协整。如果μ1t设定为(2)式的TAR模型，则认为是两机制的阈值协整；如果是(3)式则是三机制阈值协整。随机干扰项εt设定为：

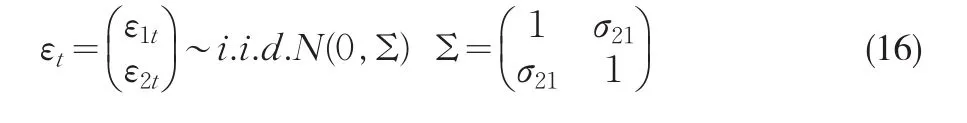
模拟中σ21分别取0、0.4和0.8，当σ21=0 时说明(15)中的解释变量是严格外生的，否则是内生变量。ε1t∼iidN(0,1)，ε2t可以通过ε1t和 Σ 的Cholesky分解而得到，样本容量分别为50和200，真实的协整参数设定为α=1,β=2，模拟中集中讨论长期参数β的估计量10000次再进行标准化，观察与标准正态分布之间的差距。在DOLS的模拟中，利用AIC准则来确定阶数K，K的最大值是不超过12(T/100)14的最大正整数(Kurozumi和 Hayakawa，2009)[10]。长期方差估计中的AR(L)的滞后阶L采用AIC准则。

在阈值协整中，为了保证数据过程中包含有阈值效应，在两机制中设定ρ1=0.4和ρ2=0.55,0.99，阈值γ=0.2；由于在模拟中发现三机制的阈值协整情形与两机制阈值协整相同，三机制阈值协整并没有包含很多信息，所以只列出了两机制阈值协整模拟结果。

3.1 各种估计的标准化量和标准正态的比较

图①是设定，取0.8时的核密度估计图，图a、b、c是ρ2=0.55，σ21分别报0、0.4和0.8；图d、e和f是ρ2=0.99，σ21分别取0、0.4和0.8，样本容量取200。

从图1可以得到：①FM-OLS和CCR估计量比其他估计量更接近标准正态，即使是在没有内生性的情况下也如此，因为其分位数更加靠近标准正态分位数；②在系数ρ2保持不变的情况下，随着σ21的增加，即内生性程度增加，OLS、CCR和DOLS估计量的分位数会增加，且都要大于对应的标准正态分位数，而FM-OLS估计量要小于相应的标准正态分位数，这说明随着内生性程度加强，OLS、CCR和DOLS有过度拒绝原假设的概率，其中OLS具有最大的拒绝概率，而FM-OLS有过度接受原假设的概率，增加速度由快到慢的顺序是OLS→DOLS→CCR→FM-OLS；③σ21保持不变时，随着参数ρ2的增加，各估计量的分位数呈增加趋势，尤其OLS估计量的分位数增加更快，所以各方法有过度拒绝原假设趋势，OLS法拒绝原假设的概率最大，增加速度由快到慢的顺序也是OLS→DOLS→CCR→FM-OLS。

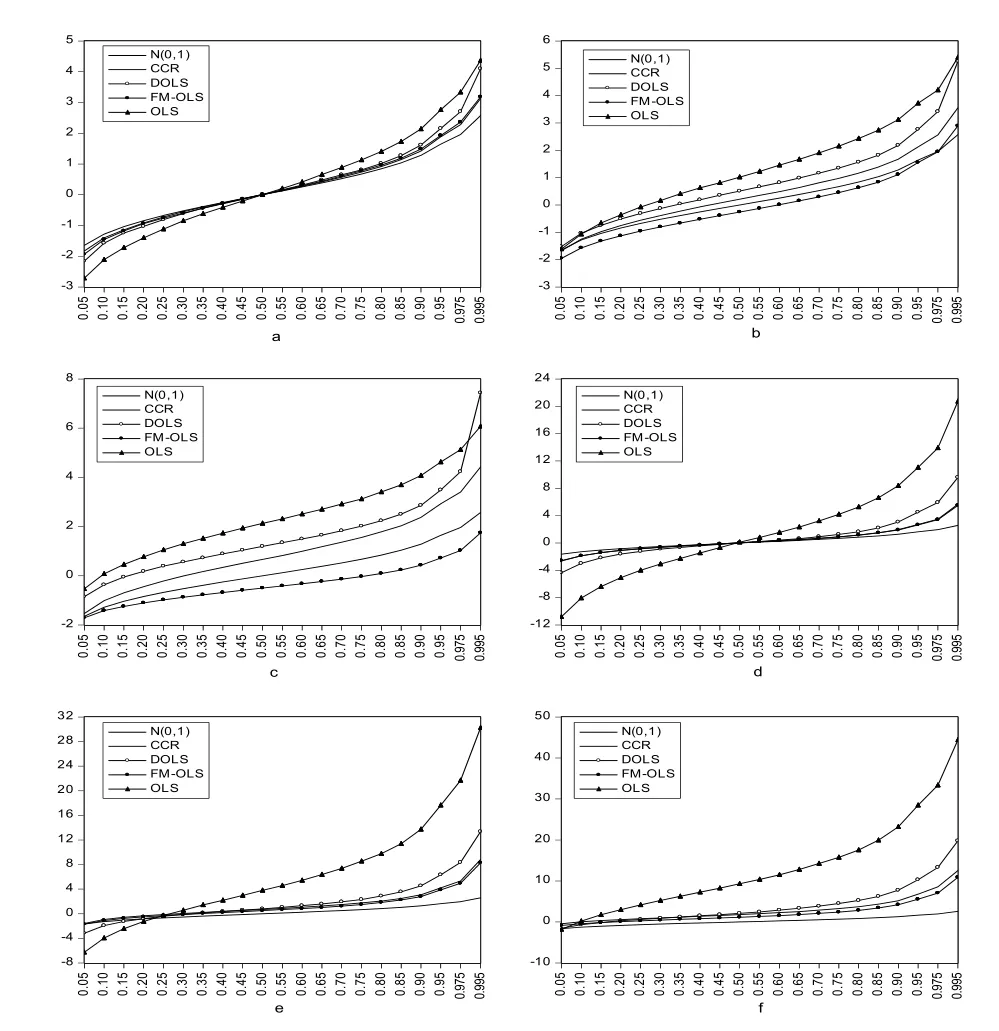
图1 各种估计量的分位数与标准正态分布分位数的对照图

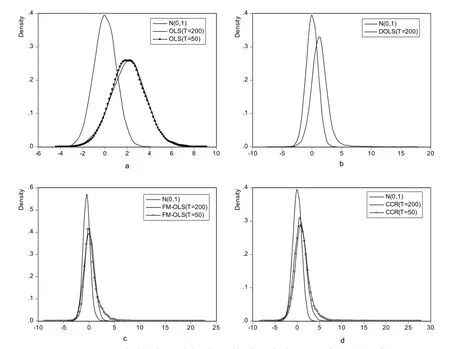
图2 各估计量的核密度估计图与标准正态图的比较

3.2 收敛到标准正态分布的速度研究

图2是设定ρ2=0.55，σ21取0.8时的核密度估计图，样本容量分别为50和200，图a是OLS估计的核密度估计，b、c和d分别是DOLS、FM-OLS和CCR的核密度估计图。在图b中没有给出T＝50时的DOLS估计分布图，主要原因是DOLS估计量在T=50时非常发散，即方差很大，在一个图中很难分辨。

从图2来看：①OLS和DOLS估计量的右偏程度较大，而FM-OLS和CCR右偏相对较小；②随着样本容量增大，收敛到标准正态的速度快到慢的顺序是FM-OLS→CCR→DOLS→OLS。值得注意的是，当T=50时，FM-OLS估计量分布很接近标准正态分布，而随着样本容量的增加，FM-OLS估计量开始左偏，说明FM-OLS估计量所构造的t统计量有可能会过度接受原假设；③随着样本容量增加，OLS估计量经验分布几乎没有发生变化，说明即使在样本容量更大时，OLS估计量构造的t统计量过度拒绝原假设的概率不会减少。

4 结论

阈值协整在交易成本和固定调节成本等经济分析中具有越来越广泛的应用，但是已有的对阈值协整参数的统计推断研究成果尤其太少，同时在阈值协整分析中常被忽略的问题是阈值协整变量的内生性问题，在实际经济分析中常常假定变量是严格外生的，这严重地违背了现实经济问题，本文也正是在这一基础上展开对阈值协整参数推断的研究。另外在具有内生性的阈值协整中，静态的OLS估计量不仅具有小样本偏差，而且由于丢弃了来自内生性变量的信息，因此基于OLS估计量的参数的约束性推断有可能存在误导。鉴于此，本文一方面研究修正的阈值协整参数估计——FM-OLS、CCR和DOLS估计及其极限分布，另一方面又在小样本条件下，MC模拟研究各标准化估计量与标准正态分布的差距。我们的模拟结果表明：①随着阈值协整的非对称程度增加和内生性程度增强，所有估计量与标准正态分布的差距会增大，增大的速度由快到慢的顺序是OLS→DOLS→CCR→FM-OLS，并且除FM-OLS估计量外，其他估计量拒绝原假设的概率也会以同样的顺序增加；②随着样本容量的增加，在其他条件不变的情况下，收敛到标准正态分布的速度由快到慢的顺序是FM-OLS→CCR→DOLS→OLS，且随着样本容量增加，FM-OLS估计量由很接近标准正态分布到越来越左偏，因此在样本容量较大时，FM-OLS极有可能会过度接受原假设；③因为随着样本容量的增加，OLS估计量的经验分布几乎不发生变化，因此无论是否存在内生性，修正估计量都比OLS估计量有优势，这说明修正的阈值协整参数估计法不仅可以减少OLS估计量的小样本偏差，而且也能更加准确地进行参数的约束性检验。

综上所述，在应用阈值协整进行经济学分析时，由于实际经济中样本容量的限制，我们认为无论是协整参数的估计，还是参数的约束性检验，都应该首选FM-OLS方法，其次是CCR方法，而其他方法如DOLS法和OLS法都存在较严重的过度拒绝原假设倾向，即具有较严重的检验水平扭曲。

[1]Nathan S.Balke，Thomas B.Fomby.Threshold Cointegration[J].International Economic Reviews,1997,38（3）.

[2]刘汉中.Ender-Granger方法在协整检验中的应用研究[J].数量经济技术经济研究,2007，(8).

[3]Chan,K.S,Petruccelli,J.D.,H.Tong.A Multiple Threshold Model AR(1)Model[J].Journal of Applied Probability,1985,22(2).

[4]Frederique Bec,Melika Ben Salem，Marine Carrasco.Tests for Unit-root Versus Threshold Specification with an Application to the Purchasing Power Parity Relationship[J].Journal of Business&Economic Statistics,2004,22(4).

[5]Whitney K.Newey,Kenneth D.West.A Simple,Positive Semi-definite,Heteroskedasticity and Autocorrelation Consistent Covariance Matrix[J].Econometrica,1987,（3）.

[6]Newey Whitney,Kenneth West.Automatic Lag Selection in Covariance Matrix Estimation[J].Review of Economic Studies,1994,61(4).

[7]W.J.Den Haan，Andrew Levin.Inferences from Parametric and Non-parametric Covariance Matrix Estimation Processes[C].Technical Working Paper,National Bureau of Economic Research,1996.

[8]Ng and Perron.Unit Root Tests in ARMA Models with Data-dependent Methods for the Selection of the Truncation Lag[J].Journal of the American Statistical Society,1995,90(1).

[9]刘汉中，李陈华.阈值协整参数修正估计法的小样本性质比较研究[D].工作论文，2010.

[10]E.Kurozumi，K.Hayakawa.Asymptotic Properties of the Efficient Estimators for Cointegrating Regression Models with Serially Dependent Errors[J].Journal of Econometrics,2009,149，（2）.