CGE模型中CES生产函数的贝叶斯估计

杨珂玲，葛翔宇，石玮玮

（1.中南财经政法大学 统计与数学学院，武汉 430073；2.湖北经济学院统计与应用数学系，武汉 430205；3.华中师范大学 经济学院，武汉 430079）

0 引言

贝叶斯统计是由T.R.Bayes于19世纪创立的数理统计的一个重要分支，20世纪50年代以H.Robins为代表提出了在计量经济学模型估计中将经验贝叶斯方法与经典方法相结合理论，得到了广泛的应用。文献[3]详细分析了经典线性计量经济学模型（正态线性单方程）的贝叶斯估计问题；文献[4]、[5]和[6]把贝叶斯方法推广到了非线性计量经济模型中，主要讨论了CES生产函数模型的贝叶斯估计问题，把CES生产函数模型通过两边取对数使其线性化，然后再利用线性计量经济学模型的贝叶斯估计方法进行分析。其中文献[4]还验证了贝叶斯估计相比传统估计方法所得的结果收敛性更好、经济意义更实际等优点。本文将进一步讨论以CES生产函数模型为例分析单个方程非线性模型的贝叶斯估计问题。本文拟采用的模型线性化方法与文献[4]、[5]和[6]的方法不同，将在CES生产函数显性化的问题上进行改进，并用此方法分析CES生产函数模型在不同的先验分布下的贝叶斯估计问题。

1 贝叶斯估计与传统估计方法的区别

贝叶斯估计是与经典估计方法相对应的一种估计方法，它的基本思路是：要估计的模型参数服从一定分布的随机变量，先根据经验给出待估参数的先验分布（主观分布），关于这些先验分布的信息称为先验信息；然后根据这些先验信息与样本信息相结合，应用贝叶斯定理，求出待估参数的后验分布；再应用损失函数，得出后验分布的一些特征值，并把它们作为待估参数的估计量。

贝叶斯估计与传统估计方法的不同之处为:

（1）参数观点的不同。经典估计方法认为待估参数θ∈Θ具有确定性。但是贝叶斯估计方法认为待估参数θ具有随机性,即在具体进行观测（得到样本x）之前，人们对θ根据过去的经验积累了一些知识。虽然θ的具体值未知，但它服从Θ上的概率分布f(θ)。该分布叫做θ的先验分布。

（2）利用的信息不同。经典方法只利用样本信息，但是贝叶斯方法要求事先提供一个参数的先验信息（一般根据专家经验提供）,即非样本信息，在参数估计过程中，这些非样本信息与样本信息一起被利用。

（3）对随机误差项的要求不同。经典方法除了最大似然法，在参数估计过程中并不要求知道随机误差项的具体分布形式，但在假设检验与区间估计及在贝叶斯估计时都要知道随机误差项的具体分布形式。

（4）选择参数估计量的准则不同。经典方法一般用最小二乘法和最大似然原理为准则，求参数估计量；但是贝叶斯估计则需要构造一个损失函数（一般采用二次损失函数），并以损失函数最小化为准则求参数估计量。

2 单方程计量经济学模型贝叶斯估计的过程

2.1 贝叶斯统计方法

定理1（离散型）设A1,A2,...An,...是一完备事件组，则对任一事件B,P(B)＞0,有：

式（1）称为贝叶斯公式。P(Ai)和P(Ai|B)分别称为原因的先验概率和后验概率。P(Ai)（i=1,2,....）是在不知道事件B是否发生的情况下诸事件发生的概率。在获得新的信息（事件B发生）后，人们对诸事件发生的概率P(Ai|B)就有了新的估计。

定理2（连续型）设θ为待估参数，θ的先验分布为g(θ)，X为样本观测信息，X的密度函数记作f(X|θ)，g(θ|X)为θ的后验分布密度函数：

其中，对θ而言 ∫θf(X|θ)g(θ)dθ是常数，即f(X)可以认为是常数。f(X|θ)在形式上同θ的似然函数L(θ|X)一致，所以（2）式可改写为：

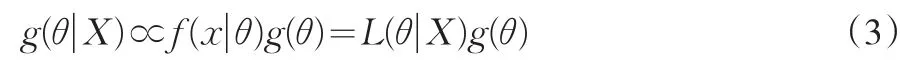
即后验信息正比于样本信息与先验信息的乘积，f(x|θ)g(θ)称为g(θ|X)的核，（3）式表明通过样本信息对先验信息的修正来得到更准确的后验信息。在得到后验分布的密度函数后，可以进行参数的点估计、区间估计和假设检验。

2.2 损失函数

取损失函数为二次函数，则得

定理3[1]待估函数h(θ)取值于R1，损失函数为L(θ,d)=λ(θ)[h(θ)-d]2，0＜λ(θ)＜∞,θ∈Θ 。则h(θ)的贝叶斯估计为：

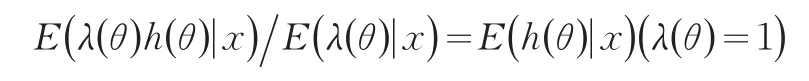
2.3 贝叶斯估计的过程

（1）确定模型的形式，找出待估参数β。

（2）给出待估参数β的先验分布。待估参数β是一个多维向量，此时需要给出多参数的联合先验信息。若无先验信息，一般可取β为均匀分布。实际上常用的先验分布为自然共轭分布，即β的密度函数（先验信息）和X密度函数（样本信息），以及两者结合后产生的函数（后验分布）服从同一分布。

利用样本信息，修正先验分布。利用贝叶斯定理2导出β的后验密度函数。

选择二次损失函数，利用β的后验密度函数和定理3，进一步推断出β的点估计。

3 常替代弹性（CES）生产函数模型的贝叶斯估计

这里我们考虑在只有资本K和劳动L两种要素下，规模报酬不变类型的常替代弹性（CES）生产函数模型：[2]

其中，Qi为第i个系统产出值，g=-ρ=(ε-1)/(ε),ε是替代弹性参数。先在（4）式两边都取g次幂，然后重排各项，得

设Y是一组n×1的向量观测值，且满足

应该强调和s2都是g的函数。且贝叶斯估计分无先验信息和先验信息两种。

(1)先验信息的贝叶斯估计

将（12）与（10）式的似然函数合并，得参数的后验分布为：

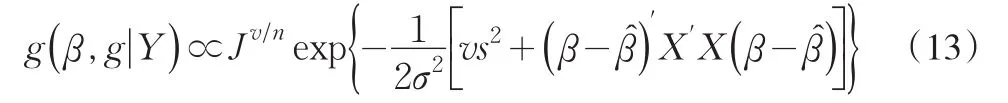
从（13）式可以看出，β的后验密度是一个3维多元正态分布，均值为。因此由定理3可得β的贝叶斯估计为。为了求得g的边缘后验密度，将（13）式对β积分，得：

式(14)是g的边缘后验密度。由定理3，根据这个密度,可用数值计算方法求出g的贝叶斯估计g。另外从（8）式容易由已有的估计和得到A,δ的估计。

(2)有先验信息的贝叶斯估计

β的先验分布为自然共轭分布,即取正态密度函数，用（13）式中的后验分布作为先验分布，为了区别这两个样本，分别用脚标1和脚标2表示，在（13）式中的后验密度可用来作为分析新样本的先验密度。即：

对第二个样本(Y2X2),其似然函数由下式给出：

其中Y2是n2×1的向量，是因变量在第二个样本中的观测值，假定第二个样本的β与第一个样本的β相同。

将（16）式的似然函数与（15）式的先验密度合并，可得

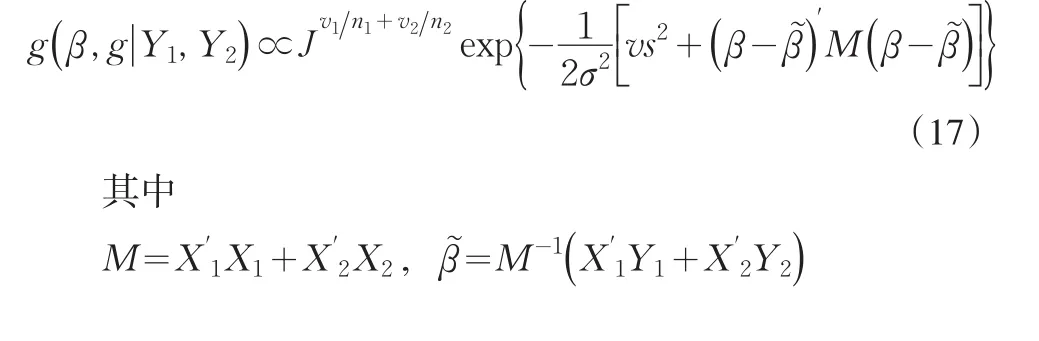
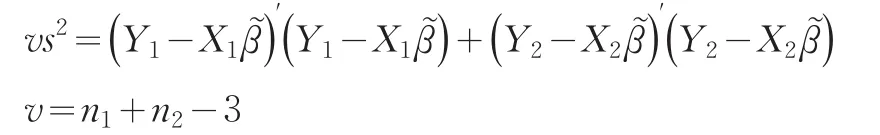
可以看出，（17）式与（13）式有完全相同的形式，因而它能用相同的方法来分析。此处假定σ2已知，但实际上σ2很少是已知的，那么当σ2未知时，CES生产函数的贝叶斯估计有待进一步讨论。

[1]陈希孺.数理统计引论[M].北京：科学出版社，1997.

[2]李子奈.高等计量经济学[M].北京：清华大学出版社，2000.

[3]李子奈.计量经济学(第二版)[M].北京：高等教育出版社，2000.

[4]徐卓顺.CGE模型：建模原理、参数估计方法与应用研究[D].吉林大学博士论文，2009.

[5]A.Hoff.The Linear Approximation of the CES Function with an Input Variables[J].Marine Resource Economics,2004,(19).

[6]L.C.Adkins,D.S.Rickman,A.Hameed.Bayesian Estimation of Regional Production for CGE Modeling[J].Journal of Regional Science,2003,43(4).