地区统计数据准确性质量的比较
2011-09-05龚敏庆孙明伟金明仲
龚敏庆,孙明伟,金明仲
(1.贵州民族学院,贵阳 550025;2.贵州大学,贵阳 550025)
0 引言
Behrens[1]-Fisher[2](B-F)问题在统计理论与应用中具有重要作用,若两个正态总体的协方差阵未知且不同,根据样本来检验两总体均值相等的检验的问题称为B-F问题。对于求解单变量B-F问题,Scheffe[3]提出了一种将初始的二样本问题转换为单总体问题的转换方法,以便通过传统的t-检验方法进行检验。Welch[4]在研究学生t-分布的基础上提出了一种近似自由度法。Bennett[5]扩展了Scheffe[3]的转换方法,用于求解多元B-F问题。Anderson[6]指出这种转换方法的优点是在检验过程中用到的样本均值向量的差异与总体均值向量差异密切相关。Welch[4]的近似自由度方法也被扩展到多元B-F问题方面。ZHANG JinTing和XU JinFeng[7]研究了高维多总体B-F问题,他们也扩展了Scheffe的变换方法,提出利用L2-检验方法于Hotelling的T2-检验方法无法使用一些场合,那是一些检验多个具有不同协方差阵的高维正态总体的均值向量是否相等的场合。
质量优良的地区统计数据,是政府制订正确方针、政策,诊断宏观经济运行好坏的有效参考,因此我国对于提高地区统计数据质量的研究和实践十分重视。对统计数据质量的研究各国和一些国际组织构建了不同的数据质量评价和管理体系。文献[8]构建了地区统计数据质量准确性方面的B-F问题,针对我国部分地区的统计数据,通过对时间序列数据的拟合建模,讨论其准确性,检验各个地区统计数据质量准确性是否存在显著性差异。本文是文献[8]研究的继续,在文献[8]的基础上对各个地区的统计数据质量的准确性差异进行评估和分析,创新要点在于对不同地区统计数据质量的准确性进行排序比较的方法,这也是讨论地区数据质量准确度可比性的一个方面。该方法也可以考虑用于统计数据质量的其他方面,使得我们可以从统计数据质量的八个方面构建统计数据质量的评估比较系统。
1 扩展Scheffe转换法[7]
我们可以用扩展Scheffe转换方法[3][7],将多总体B-F问题转换为单总体问题。单总体问题分布为:
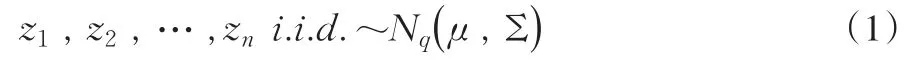
这里Nq(μ,Σ)表示均值向量为μ,协方差阵为Σ的q维正态分布。设q的值较大,μ和Σ未知。单总体问题检验假设为:

这里μ0是已知q维向量。
考虑多总体B-F问题:假设有k个独立正态总体,对于l=1,2,...,k:
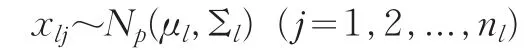
Np(μl,Σl)是均值向量为μl,协方差阵为 Σl的p维正态分布。多总体B-F问题检验k个均值向量是否相等:

这里不假定协方差阵Σl(l=1,2,…,k)相等。
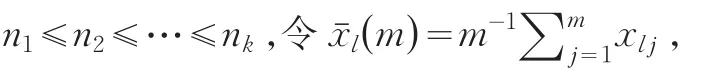
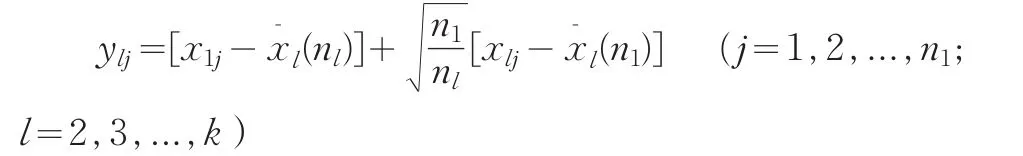
用以上Scheffe[3]方法,把后面的k-1个样本转换为单总体样本得到:

A⊗B为矩阵直积,Jk-1为所有元素均为1的(k-1)阶方阵,diag(A1,A2,…,Al)表示对角线分块矩阵分别为A1,A2,…,Al的矩阵。这样k总体B-F问题(3)的变量就转换为正态总体(4)独立同分布的单总体变量,从而可以利用单总体问题的检验方法。
由孙明伟等论文[14]可知:当q远小于n1时,此问题可以用HotellingT2-检验方法。(4)的变量是独立同正态分布的,其均值向量为:
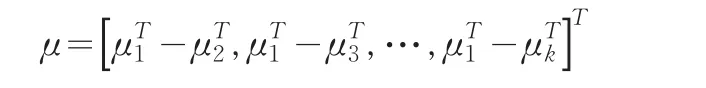
这表明μ=0当且仅当μ1=μ2=…=μk,因此k总体B-F问题关于零假设(3)的检验转化为单总体问题相应于零假设(2)的检验。μ的估计可为样本均值向量:
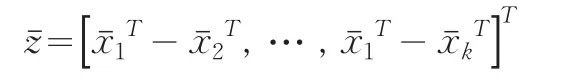
2 地区统计数据质量评估方法
对于时间序列统计数据,可根据数据的变动规律构造模型,对序列的变化趋势进行拟合,然后通过比较样本观察值与模型的预测值来评估统计数据质量。
对于非平稳的时间序列Xt,可以用Xt=f(t)+vt来描述,其中f(t)表示Xt随时间变化的均值,为序列的确定性部分;vt为Xt残差剩余部分。
质量良好的统计数据可以准确反应真实情况,并可以通过它们对未来的相应值进行有效的预测,将误差控制在有效的范围内。对统计数据准确性进行的定量分析利用统计指标的历年数据的变化特点建模,并对模型进行一系列的统计检验,在模型通过各种检验、具有良好统计预测功能的基础上,比较模型拟合出的预测值与实际观察值,计算其偏离程度。以下介绍刘洪、黄燕(2007)论文中关于评估数据质量的方法之一:相对误差法[12]。
用统计指标的当期实际值与根据模型计算出的预测值进行比较,计算出相对误差ε,第n期的相对误差为:

给定一个允许的误差范围,Xn表示实际观察值,表示拟合估计值,如果 |εn|在该误差范围内,则可初步断定统计指标的该期数据可靠,否则认为数据质量可能存在问题。允许误差范围的确定并没有一个标准,不同的误差范围可能会得出不同的评估结果。
本文中我们将采用趋势拟合评估法对所选的不同地区的经济统计数据进行拟合,比较模型拟合出的预测值与实际观察值,计算出其相对误差的绝对值对其数据质量进行评估,并构建地区经济统计数据质量的多总体B-F问题,讨论相应的地区经济统计数据质量准确性是否具有显著性差异并进行排序比较。
3 实证研究
我们还是选取三个反映经济发展情况的重要指标来对其数据质量进行评估,即地区生产总值(GDP)、全社会固定资产投资总额(FAI)和城镇居民最终消费支出(FCE),并运用求解多总体B-F问题的方法对地区间部分有关经济统计数据的数据质量进行检验,研究它们是否具有显著性差异并对其质量准确性进行比较排序。
对于政府有关经济方面的统计,大多用不变价格来计算发展速度。本文中选取地区自1999~2008年间相关指标的统计数据,但并未对其用不变价格换算系数进行换算,因为文中所构建的B-F问题是对地区间的统计数据质量是否有显著性差异进行检验,并用观察值与预测值间相对误差的绝对值来反映数据质量的好坏,并没有利用这些数据对地区间的经济发展情况或是总产值的大小进行直接的比较,所计算出的结果都是相对值。因此,用现价对我们的问题并没有影响。
我们对1999~2008年间关于三个省市,简称为B市、G省、和Y省分别选取上述相关指标的国家统计局公布的统计数据,这些数据均来自国家统计局所出版的《中国统计年鉴~2009》[9],并运用趋势拟合评估法对相关指标的趋势进行拟合,利用拟合方程分别求出相应年份的拟合值,并计算其相对误差的绝对值得到衡量其数据质量的指标数据,构建地区统计数据质量多总体B-F问题,分别比较三省市地区统计数据质量准确性是否存在显著性差异并对其准确性质量进行排序对比检验。
对B市和Y省,用Matlab软件对其时间序列地区统计数据作图得图1。由图1可知,这三个指标序列与大多数的经济序列一样,是非平稳的,近似呈指数上升的趋势,因此我们选择指数模型来拟合上述三个指标的趋势增长。
这里我们用Matlab软件分别求出B市和Y省关于三个统计指标的实际观察值与时间t之间的拟合方程后,再将相应的年份代入求得的方程,分别求出相应年份各指标的拟合值,并将拟合值与相应的实际观察值代入公式(1),计算出该年份下相应指标的相对误差,并取其绝对值,它们的大小反映了该地区相应年份对应统计数据质量的准确性。例如由图1知B市1999~2008年间GDP随时间t的增加呈指数增长,由Matlab得B市GDP的以下拟合公式:
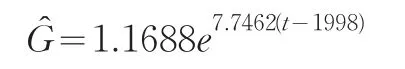
然后将年份时间t分别代入上述方程求出B市该年的GDP拟合值,根据B市该年相应的GDP的实际观察值G,将G与拟合值代入公式(6),计算出相应的相对误差值ε,并取其绝对值 ||ε,得到如表1的B市GDP相对误差绝对值数据。用同样的方法得到各地区关于相应的指标的拟合公式,计算出B市、Y省和G省这三个市省的地区生产总值(GDP)、全社会固定资产投资总额(FAI)、城镇居民最终消费支出(FCE)等三个统计指标关于1999到2008年等年份相对误差值的绝对值,由此得到表1。
然后可以用二总体B-F问题来讨论,我们用上文中介绍的求解B-F问题的扩展Scheffe[3]转换法,将此二总体问题转换为单总体问题:
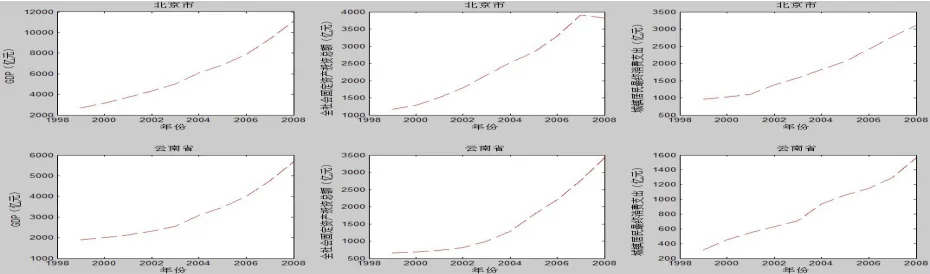
图1 B市和Y省部分经济统计数据
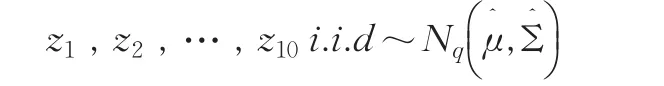
由以上数据得到μ和Σ,然后可以用二总体B-F问题来讨论,我们用求解B-F问题的扩展Scheffe[3]转换法,将此二总体问题转换为单总体问题:
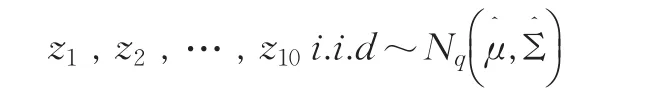
由以上数据得到μ和Σ的估计如下:
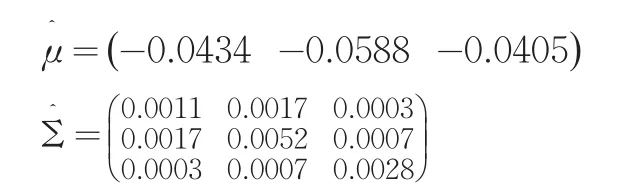
其样本容量n=10,维数q=3。再用霍特林T2-检验方法对其进行均值向量检验:

取检验统计量:
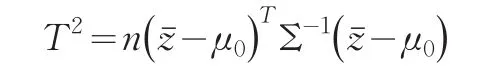
经计算得:T2=20.1067
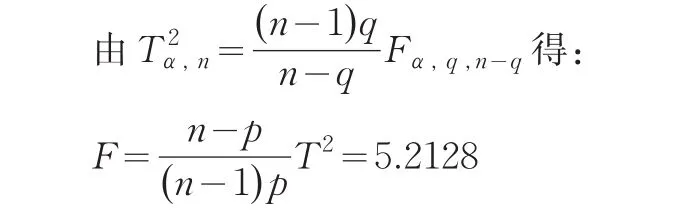
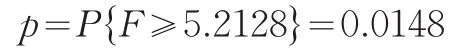
对于给定的显著性水平α=0.05下,经Matlab软件计算得其p值为(此时检验统计量F~F(3,7):因p=0.0148<0.05=α,故要拒绝H0,即不能接受B市和Y省的经济统计数据质量准确性没有显著性差异的假设,两者间存在显著性差异。
进一步,我们对它们的统计数据质量准确性排序进行判断和检验,这是本文的要点。为了对两地区的三个经济指标的准确性排序,分别进行判断检验,我们提出比较其相对误差绝对值的样本均值大小的原假设
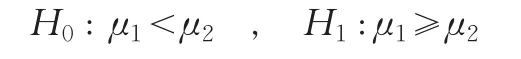
这里μ1、μ2分别表示B市和Y省的相应地区经济指标统计数据相对误差绝对值均值。
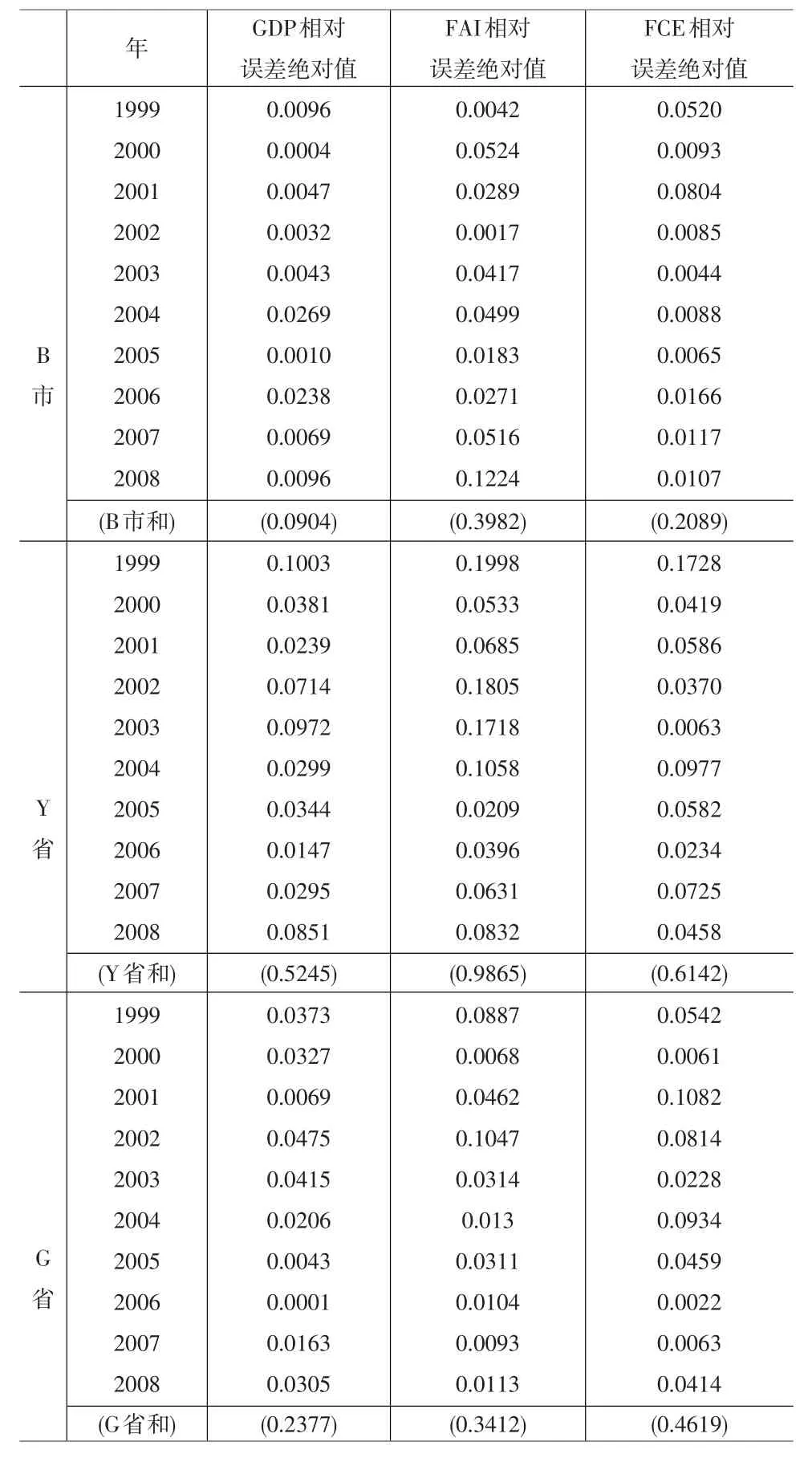
表1 1999~2008年三省市部分统计数据相对误差绝对值
对于给定的显著性水平α=0.05,利用Mat lab软件进行计算,计算结果中引入参量[H,p],H=0表示在显著性水平α下,不能拒绝原假设,H=1表示在显著性水平α下,可以拒绝原假设;p为当原假设为真时得到观察值的概率,当p为小概率时则对原假设提出质疑。
原假设为B市地区统计数据质量优于Y省,即B市的此三个经济指标统计数据绝对误差的平均值分别小于Y省,即:H0:μBi<μYi,H1:μBi≥μYi(i=1,2,3),由 T 统 计 量 、Matlab计算得出此假设检验结果如下:
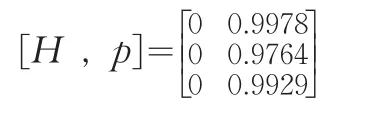
由Hi均等于0,pi值均接近于1可以看出,B市的地区统计数据质量优于Y省的相应地区统计数据质量。
同样的,我们对B市和G省的地区统计数据的准确性进行比较。首先计算其相应指标相对误差的绝对值,得到G省的数据质量准确性数据(见表1)。
利用扩展Scheffe[3]转换法,将由B市和G省的地区统计数据的相对误差绝对值构成的二总体B-F问题转换为单总体问题:
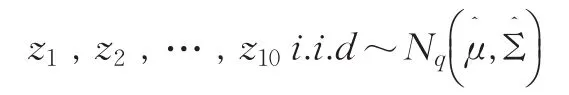
由以上数据得到μ和Σ的估计:
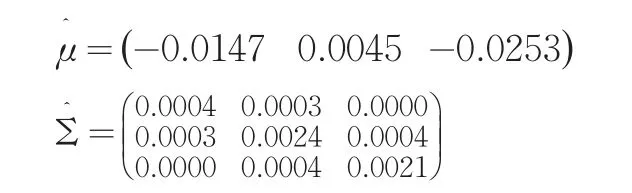
用霍特林T2-检验方法对其进行均值向量检验:
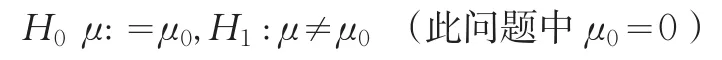
对于给定的显著性水平α=0.05下,p=P{ }F≥2.9961=0.0637因p=0.0637>0.05=α,故接受原假设H0,即B市和G省的经济统计数据质量没有显著性差异。如果取α=0.1,则接受B市和Y省的统计数据准确性质量有显著性差异假设。
进一步,我们对它们的统计数据质量的优劣进行判断和检验,对这两地区的三个经济指标的准确性大小分别进行判断检验,比较其相对误差绝对值的样本均值大小。原假设为B市地区统计数据质量优于G省,即
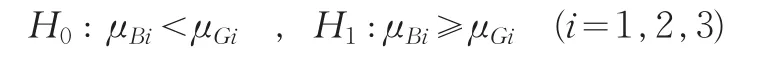
对于给定的显著性水平α=0.05下,利用Matlab软件进行计算,如同上面分析B市和Y省地区统计数据质量的优劣性,经HotellingT2-分布计算得出此假设检验结果为:
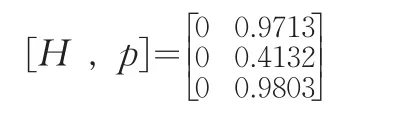
由上述结果可以看出,B市的地区统计数据质量优于G省的相应地区统计数据质量。
继而,我们对G省和Y省的地区经济统计数据质量进行相应的分析,得出由它们的相对误差绝对值构成的二总体B-F问题转换为单总体问题的μ和Σ的估计:

用霍特林T2-检验方法对其进行均值向量检验:
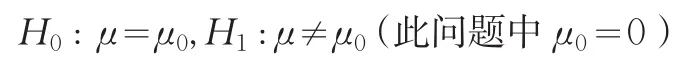
经计算得检验统计量:
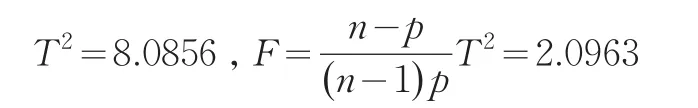
对于给定的显著性水平α=0.05下:
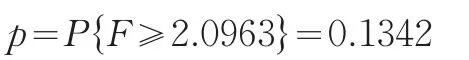
因p=0.1342>0.05=α,故接受原假设H0,即G省和Y省的经济统计数据质量没有显著性差异,但是0.1342与0.05接近,如果取α=0.1虽然也接受G省与Y省统计数据准确性质量没有显著性差异,但0.132与0.1很接近,0.132处于临界的区域,使得没有显著性差异的检验结果难以接受也不好拒绝。
这时如果对它们的统计数据质量准确性的优劣进行判断和检验,对该两地区的三个经济指标的准确性大小分别进行判断检验,比较其相对误差绝对值的样本均值大小。原假设为G省地区统计数据质量优于Y省,即
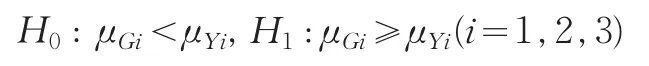
对于给定的显著性水平α=0.05下,利用Matlab软件进行计算,经计算得出此假设检验结果为:
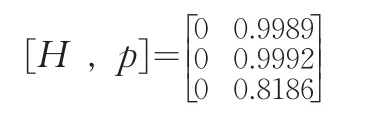
由上述结果可以看出,G省的地区统计数据质量优于Y省的相应地区统计数据质量。通过以上分析检验可得,此三地区的地区统计数据质量的好坏依次为B市优于G省优于Y省。
4 结论
本文对B市、G省和Y省经济统计数据中的地区生产总值(GDP)、全社会固定资产投资总额(FAI)、城镇居民最终消费支出(FCE)统计数据的数据质量的研究,构建地区统计数据B-F问题,检验了三地区上述经济指标的统计数据质量准确性是否具有显著性差异,并对其准确性差异进行了对比和检验,得出统计数据质量准确性顺序为B市准确性≻G省准确性≻Y省准确性。进一步的研究可以将该方法用于对同一个地区的统计数据质量准确性做历史阶段比较;也可将该方法用于各个地区的统计数据准确性排序比较,以便将各个省市区的数据质量评价为几个数据质量准确性等级;另外可以考虑克服量化困难将该方法用在统计数据质量八个方面[8]的其他方面,因此该方法对于提高统计数据质量的准确性外的其他方面也有着一定的意义和作用。
[1]BV Behrens.Ein Beitrag zur Fehlerberechnung Bei Wenige Beobachtungen[J].Landwirtch.Jb,1929,(6).
[2]RA Fisher.The Fiducial Argument in Statistical Inference[J].The An nals of Eugenics,1935,(6).
[3]Scheffe H.On Solutions of the Behrens-Fisher Problem,Based on the T-distribution[J].Ann Math Statist,1943,(14).
[4]Welch B L.The Generalization of Student’s Problem when Several Different Population Variances are Involved[J].Biometrika,1947,(34).
[5]Bennett B M.Note on a Solution of the Generalized Behrens-Fisherproblem[J].Ann Inst Statist Math,1951,(2).
[6]Anderson T W.An Introduction to Multivariate Statistical Analysis[M].New York:Wiley,1984.
[7]Zhang JinTing,Xu JinFeng.On the K-sample Behrens-Fisher Problem for High-dimensional Data[J].Science in China Series A:Mathematics,2009,(6).
[8]孙明伟,龚敏庆.地区统计数据质量B-F问题研究[C].淄博第二届信息、电子计算机工程国际学术会议论文集,2010,(11).
[9]中华人民共和国国家统计局.中国统计年鉴-2009[M].北京:中国统计出版社,2009.
