构架式空间可展开天线结构优化参数预测模型

邓宗全，田大可，刘荣强，郭宏伟

(1.哈尔滨工业大学 机器人技术与系统国家重点实验室，150001哈尔滨，tdk724@126.com;2.哈尔滨工业大学 机电工程学院，150001哈尔滨)

空间可展开天线是随着航天科技的发展而产生的一种新型空间结构，由于其结构形式灵活，应用领域广泛，目前已经成为空间可展开结构中研究最活跃的一个分支[1－3].刚度和质量是评价可展开天线结构性能的重要参数，在进行天线设计时需要进行优化，但天线是一个由刚性杆件与柔性拉索构成的复杂系统，很难直接建立设计变量与刚度和质量之间的解析表达式，这给优化设计带来了很大的难度.因此建立设计变量与目标函数的映射关系是进行优化的前提和基础，有必要对这一问题进行研究.

神经网络具有通过学习逼近任意非线性映射的能力，可以不受非线性模型的限制，是非线性系统建模与应用的一个重要方法.BP神经网络是利用非线性可微分函数进行权值训练的多层前馈网络，它广泛应用于模式识别、函数逼近、数据压缩等领域，是目前应用最为广泛的一种神经网络[4].

本文基于BP神经网络对由7个模块组成的构架式可展开天线进行了研究.根据天线结构及背架的几何模型[5]，运用有限元软件ANSYS对背架进行了数值模拟，得到了与设计变量对应的目标函数值，构建了用于神经网络训练和检验的样本集，按照BP算法的基本思想，建立了目标函数的预测模型，验证了网络的泛化能力.

1 天线结构及展开原理

构架式可展开天线采用模块化思想设计，天线由7个尺寸相等的模块组成，其结构如图1所示.这种设计的优点是杆件的类型大大减少，加工和调试的时间短，制造成本低.天线的每个模块又分为金属反射网和背架两个主要部分[6－7].金属反射网成抛物面形状，起到发射和接收信号的作用.背架是模块的骨架，用来支撑反射网，它具有很高的刚度和展开精度，展开时呈六棱柱状态.交叉拉索起到维持结构稳定、提高结构强度的作用.

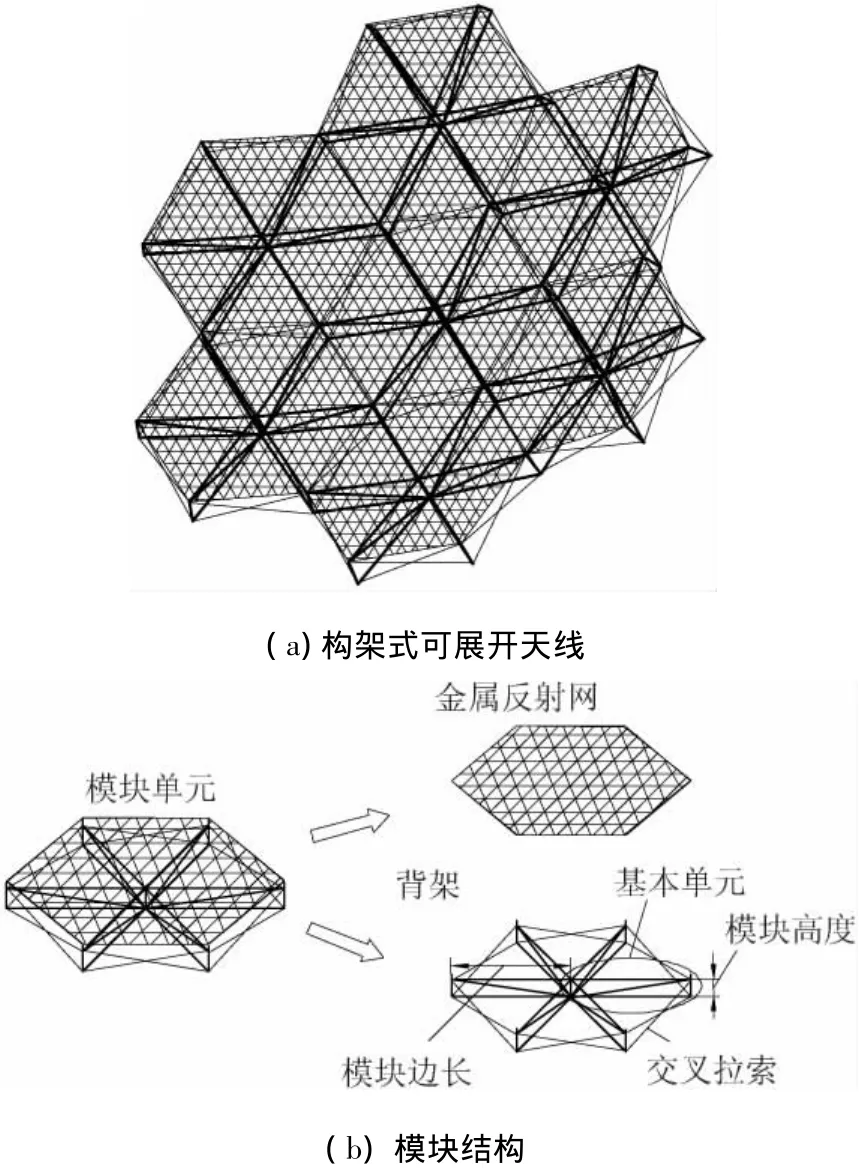
图1 构架式可展开天线及模块的结构

天线背架的展开原理与伞的张开原理类似[8]，背架由6个成辐射状发散的基本单元组成，基本单元是背架的最小可展单元.基本单元的结构如图2所示，它由电机、绳索、铰链、拉伸弹簧及各种杆件等组成.驱动力由位于中心杆上的弹簧提供，滑块与弹簧相连，能在中心杆上上下移动.模块在收拢状态时，弹簧处于被拉伸状态，当天线展开时，电机通过释放绳索来控制天线的展开速度，当弹簧恢复至自然长度时，锁紧机构将滑块锁死，天线完全展开，整个背架变成一个稳定的结构.

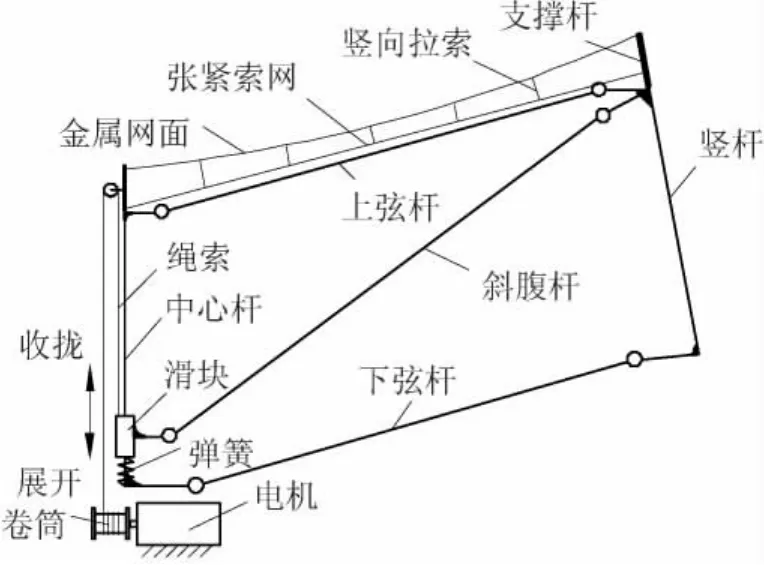
图2 基本单元

2 BP神经网络预测模型

2.1 BP神经网络的基本原理

BP神经网络即误差反向传播神经网络，是一种由大量神经元相互连接而组成的复杂网络系统，目前在各个领域中都有广泛应用.BP神经网通常由输入层、隐层和输出层组成，上、下层各神经元之间实现全连接，即下层的任意一个神经元与上一层的神经元都实现连接，而每层各神经元之间无连接[9].BP算法的学习分为信号的正向传播与误差的反向传播两个过程.正向传播时，样本由输入层传入，经各隐层处理后，传向输出层.若输出层的实际输出与期望输出存在偏差，则进入误差的反向传播阶段，即将输出误差通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据.通过这种正反向的传播过程，网络的权值不断得到调整，直到网络输出误差减小到可以接受的程度，或者进行到预先设定的学习次数为止[10].

含有一个隐层的三层神经网络具有较小的网络规模且通常能够准确地按精度要求逼近给定的函数，其网络模型如图3所示.

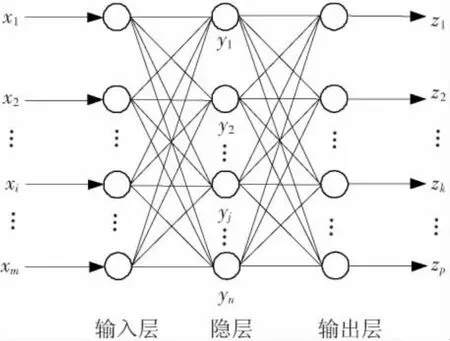
图3 三层BP网络模型

其训练过程如下[10－11]:

设一组输入信号为 x1，x2，…，xi，…，xm;隐层输出信号为y1，y2，…，yj，…，yn;输出层信号为z1，z2，…，zk，…，zp;期望输出为 Z1，Z2，…，Zk，…，Zp;输入层到隐层之间的权值为vij，隐层到输出层之间的权值为wjk，隐层神经元的阈值为αj，输出层神经元的阈值为 βk，其中，i=1，2，…，m;j=1，2，…，n;k=1，2，…，p.

首先给各层的权值、阈值赋予一个较小的随机值.

当样本进入到输入层，经过信号的正向传递，得到隐层和输出层的信号分别为

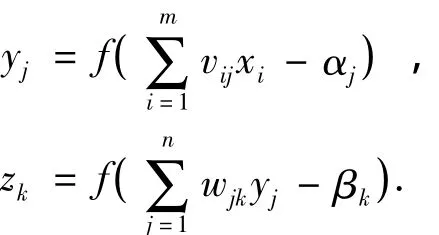
式中f(·)为传递函数，常用的有Sigmoid和对数Sigmoid等函数.

当输出层信号与期望输出不等时，输出误差为

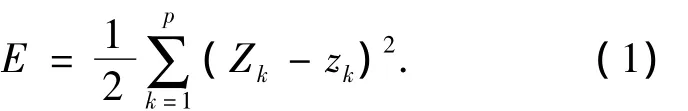
将式(1)逐层展开

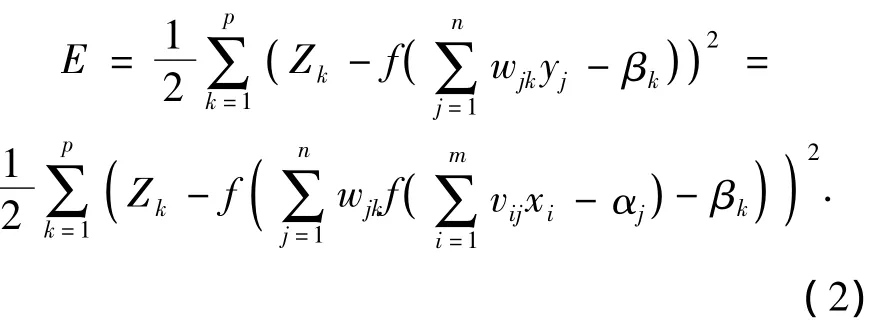
由式(2)可见，网络的输出误差是一个包含权值和阈值的函数，通过调整网络的权值和阈值可以减小输出误差，使误差沿梯度方向下降，经过反复学习训练，当达到误差要求时，训练过程结束.

2.2 网络模型的建立

由背架的结构及展开原理可知，上弦杆、下弦杆、竖杆、斜腹杆、中心杆和交叉拉索是背架的主要结构，由于上弦杆和下弦杆的受力形式及截面尺寸基本相同，因此本文将它们作为同一类杆件进行分析，统称为弦杆，那么，整个结构便简化为5部分，它们共同对结构的刚度及质量产生影响，本文着重研究对结构刚度影响最大的一阶固有频率.因此，选择弦杆直径、斜腹杆直径、拉索直径、中心杆直径和竖杆直径5个设计变量作为神经网络的输入，结构的一阶固有频率及质量2个目标函数作为网络的输出，采用三层神经网络来构建预测模型，如图4所示，图中x1～x5分别表示弦杆直径、斜腹杆直径、拉索直径、中心杆直径和竖杆直径，f1和m分别表示结构的一阶固有频率及质量.5个变量的取值范围分别为:x1=6，7，…，14 mm;x2=6，7，…，14 mm;x3=1.5，2，…，5.5 mm;x4=10，11，…，18 mm;x5=6，7，…，14 mm.各杆件的壁厚均为1 mm.

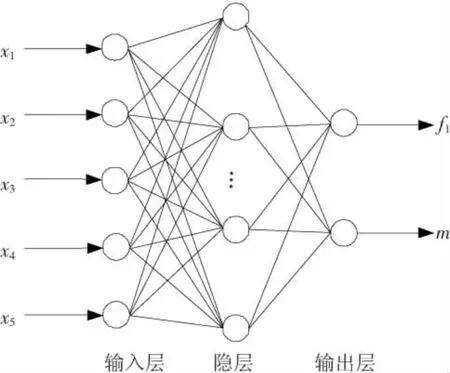
图4 神经网络预测模型

2.3 训练样本的确定

训练数据的准备工作是网络设计与训练的基础，数据选择的科学合理性以及数据表示的合理性对于网络设计具有极为重要的影响[10].本文中5个因素各有9个水平，取其中的5个水平作为训练样本，若进行全面试验，需要做55=3 125次试验，显然工作量是很庞大的，且需要花费大量的时间.为了保证训练样本能够具有一定的遍历性、致密性和容错性，本文采用正交试验设计方法，它能有效处理这种多因素多水平试验，它是利用正交表科学地安排与分析多因素试验的方法，能够大幅度减少试验次数而且不会降低试验可行度.

正交表具有两个重要性质[12]:

1)每一列中，不同的数字出现的次数相等.

2)在任意两列中，将同一行的两个数字看成有序数对时，每种数对出现的次数是相等的.

以上两点充分体现了正交表的两大优越性，即“均匀分散，整齐可比”.

试验的因素及其水平值见表1.

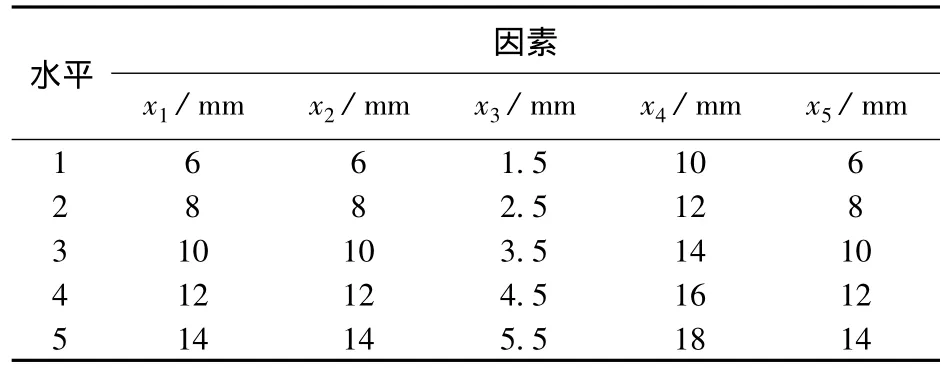
表1 试验因素和水平

根据试验的因素数和水平数，选用L25(56)正交表安排试验方案，共得到25组样本，如表2所示.

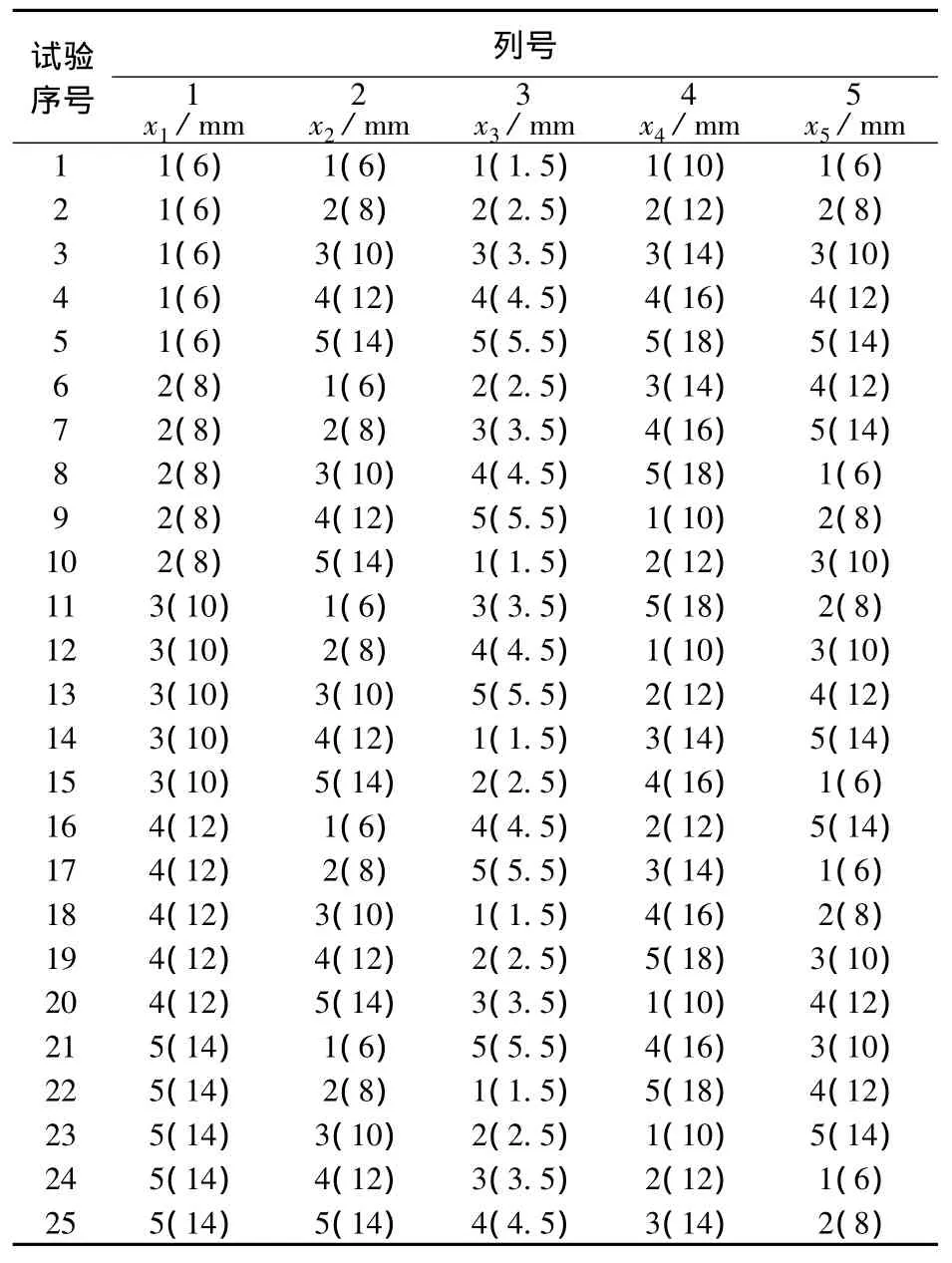
表2 正交试验设计

2.4 网络参数的确定

按照背架的几何模型，编写ANSYS软件的有限元程序，分别计算每组试验方案下的一阶固有频率和质量，将这些输入输出参数作为神经网络的训练样本.由于BP神经网络的训练过程比较复杂，本文运用MATLAB软件进行求解，在软件中编写该预测模型的算法程序，设置训练误差为0.001，为保证建立的网络模型具有较好的预测精度，应在训练过程中着重注意网络的收敛性.

影响BP神经网络收敛性的主要环节有最大训练步数、训练算法和隐层节点数等.

最大训练步数决定了训练空间的大小.当误差满足规定要求时，即使未达到最大步数也将停止训练，返回训练结果;反之，即使网络本身具有收敛性，但由于最大步数设置过小，训练在达到最大步数时也将被迫停止.因此通常应给定足够大的训练步数.

训练算法对网络的收敛速度有较大影响，通常的算法有标准BP算法、带动量的梯度下降算法、学习速率可变算法和L－M(Levenberg－Marquardt)算法等.L－M算法是建立在一种优化方法基础上的训练算法，与其它算法相比，L－M算法优点在于网络权值数目较少时收敛非常迅速.因此本文采用这种算法来训练网络.

隐层节点数通常会对训练误差、训练时间和泛化能力等产生较大影响.隐层节点数过少时，学习的容量有限，网络难以描述样本中蕴含的复杂关系;而过多的隐层节点不仅增加了训练时间，还可能把样本中非规律性的内容存储起来，出现过拟合的现象.一般采取的方法是试凑法.

在对来自实际数据的样本进行预测时，样本具有很大的随机性和不均匀性，这就对BP网络提出了更高的要求.首先，在建立网络时应尽可能地选取更多的样本，力求样本中包含更多的内在规律;其次，在确定训练算法和隐层节点数时，应尝试参数的不同组合，多次的试算，建立相对满意的网络模型.

综上，经多次反复的训练，当传递函数分别采用Sigmoid函数和线性函数，训练算法采用L－M算法，隐层节点数采用16个时构成的神经网络输出误差最小，此时网络的结构为5－16－2.经过15次训练误差达到0.000 14＜0.001，满足要求，误差曲线如图5所示.

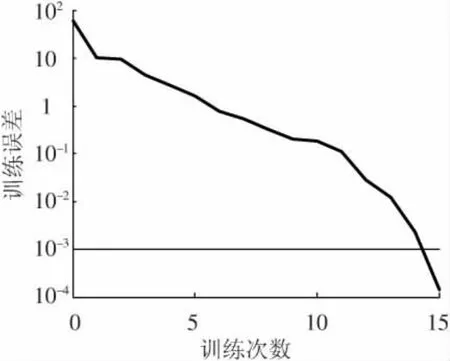
图5 误差曲线

3 泛化能力检验及结果分析

训练后的神经网络是否具有实际意义及应用价值，主要看其是否具有良好的泛化能力，即对训练样本以外的样本是否能够做出较准确的预测.在输入变量的整个取值范围内将其随机组合，选取其中的10组作为检验样本，用检验样本对训练好的神经网络进行泛化能力测试，得到频率和质量的预测值，将二者分别与有限元数值模拟结果进行对比，如表3所示.

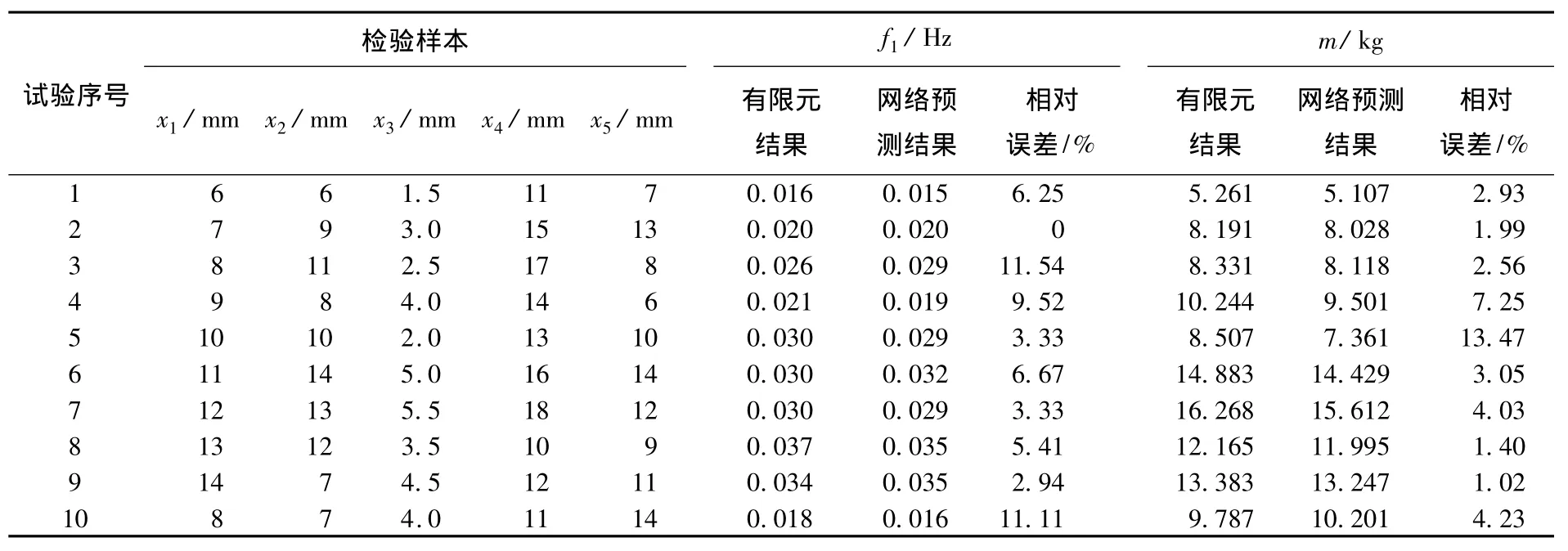
表3 网络预测结果与有限元结果对比

由表3可见，在对一阶固有频率进行预测时，除第3个和第10个样本的预测误差较大外，其余各样本的误差准确率都在90.48%以上;神经网络对质量的预测能力好于对一阶固有频率的预测能力，除第5个样本的预测误差较大外，整体的预测准确率达到92.75%以上，可见该预测模型能够较真实地反映设计变量与目标函数之间的映射关系.

在Pentium(R)D CPU3.0 GHz，2 GB 内存的计算机上进行运算，用ANSYS计算10个检验样本的时间约为700 s，而用本文提出的方法仅需0.13 s，可见BP神经网络模型的运行时间短，效率高.另外，在后续的结构优化阶段，该网络模型可以很方便地被 MATLAB、Isight等软件进行调用.

4 结论

1)采用正交试验设计的方法确定训练样本，可以保证数据选取的合理性，并减少试验次数.

2)通过对模型的泛化能力检验，发现该模型对一阶固有频率的预测能力要略差于对质量的预测，但二者的预测结果都比较理想.

3)泛化能力检验结果表明:训练好的神经网络对一阶固有频率和质量的预测精度较高，泛化能力强，该方法为结构参数的优化提供了理论基础.

4)在实际工程应用中，采用训练好的BP神经网络对结构参数进行预测具有预测精度高、预测速度快、预测范围广等突出特点，同时MATLAB等软件提供了计算函数和友好的工具箱等便利的使用平台，使得BP神经网络具有很强的可操作性，大大地方便了科研人员的使用.

[1]MEGURO A，HARADA S，WATANABE M.Key technologies for high-accuracy large mesh antenna reflectors[J].Acta Astronautica，2003，53(11):899－908.

[2]TIBERT G.Deployable tensegrity structures for space applications[D].Stockholm:Royal Institute of Technology，2002:16－31.

[3]TIAN D K，LIU R Q，DENG Z Q，et al.Analysis of dynamic characteristics of space deployable antenna based on ANSYS[J].Applied Mechanics and Materials，2010，37－38:127－130.

[4]周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社，2006:69－100.

[5]TIAN D K，LIU R Q，DENG Z Q.Spatial geometry modeling of truss structure and analysis of connection deviation for deployable truss antenna[C]//Proceedings of International Conference on Measuring Technology and Mechatronics Automation.NJ，USA:IEEE，2010:427－432.

[6]MEGURO A，ISHIKAWA H，TSUJIHATA A.Study on ground verification for large deployable modular structures[J].Journal of spacecraft and rockets，2006，43(4):780－787.

[7]NATORI M C，HIRABAYASHI H，OKUIZUMI N，et al.A structure concept of high precision mesh antenna for space VLBI observation[C]//43rd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference.Denver，Colorado，USA:AIAA，2002:1－8.

[8]MIYASAKA A，HOMMAT M，TSUJIGATA A.Design and ground verification of large deployable reflector[C]//42th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference and Exhibit.Seattle，WA，United states:AIAA，2001:2222－2227.

[9]彭熙伟，杨会菊.液压泵效率特性建模的神经网络方法[J].机械工程学报，2009，45(8):106－111.

[10]施彦，韩力群，廉小亲.神经网络设计方法与实例分析[M].北京:北京邮电大学出版社，2009:23－76.

[11]郭亚娟.空调配管系统的减振研究与阻尼优化设计[D].上海:上海交通大学，2010:83－89.

[12]李云雁，胡传荣.试验设计与数据处理[M].北京:化学工业出版社，2005:79－113.