高超声速飞行器改进自抗扰串级解耦控制器设计

齐乃明，秦昌茂，宋志国

(哈尔滨工业大学 航天学院，150001哈尔滨，1011820111@163.com)

高超声速飞行器具有重要的军事意义，近年来成为各国研究的热点[1]，无动力再入过程中具有的复杂非线性、控制通道间强耦合及气动参数不确定性等增加了控制器设计的困难.目前设计的鲁棒控制[2－3]、自适应控制[4－6]、滑模控制[7－9]等方法中，要么被控系统的线性化模型包含复杂的高阶李导数函数，不便于工程实际应用，要么要求不确定性上界为已知或是为状态变量的已知函数，这在实际应用中很难预知，并且传统的内外环控制技术忽略了内环对外环的耦合影响.

自抗扰控制器[10－12](ADRC)不依赖于系统模型，而是一种依靠过程误差来消除误差的方法，通过扩张状态观测器(ESO)估计“总和扰动”来获得对象模型中的内扰和外扰的实时作用量，并进行实时动态反馈补偿，实现系统的线性化，又采用了非线性反馈控制律(NLSEF)来抑制补偿残差，提高控制性能.但是设计中采用的连续非光滑fal函数为理想函数，并且由于其非光滑的特性，容易引起高频颤振的产生，不便于工程实际应用.

本文首先通过构造qin函数实现连续光滑扩张状态观测器，避免了自抗扰控制器高频颤振的产生.继而在高超声速飞行器无动力再入姿态非线性模型基础上，设计自抗扰串级解耦姿态控制器.将不确定项、未建模动态、飞行器通道间耦合、参数摄动等影响作为“总和干扰”利用连续光滑ESO进行估计并动态反馈补偿，再利用连续光滑NLSEF抑制补偿残差，依靠自抗扰不依赖模型的特点，解决了模型复杂线性化及滑模控制需要摄动界的问题，按照ESO稳定性条件选择参数，可以获得良好的动态品质和跟踪性能，并能够克服耦合及气动参数大范围摄动的影响，具有较强的鲁棒性.

1 高超声速飞行器姿态模型

设状 态 变 量 x1= [α β γc]T，x2=[ωxωyωz]T，控制量 δ = [δeδaδr]T，则高超声速飞行器无动力再入姿态模型为如下包含不确定项的非线性系统:

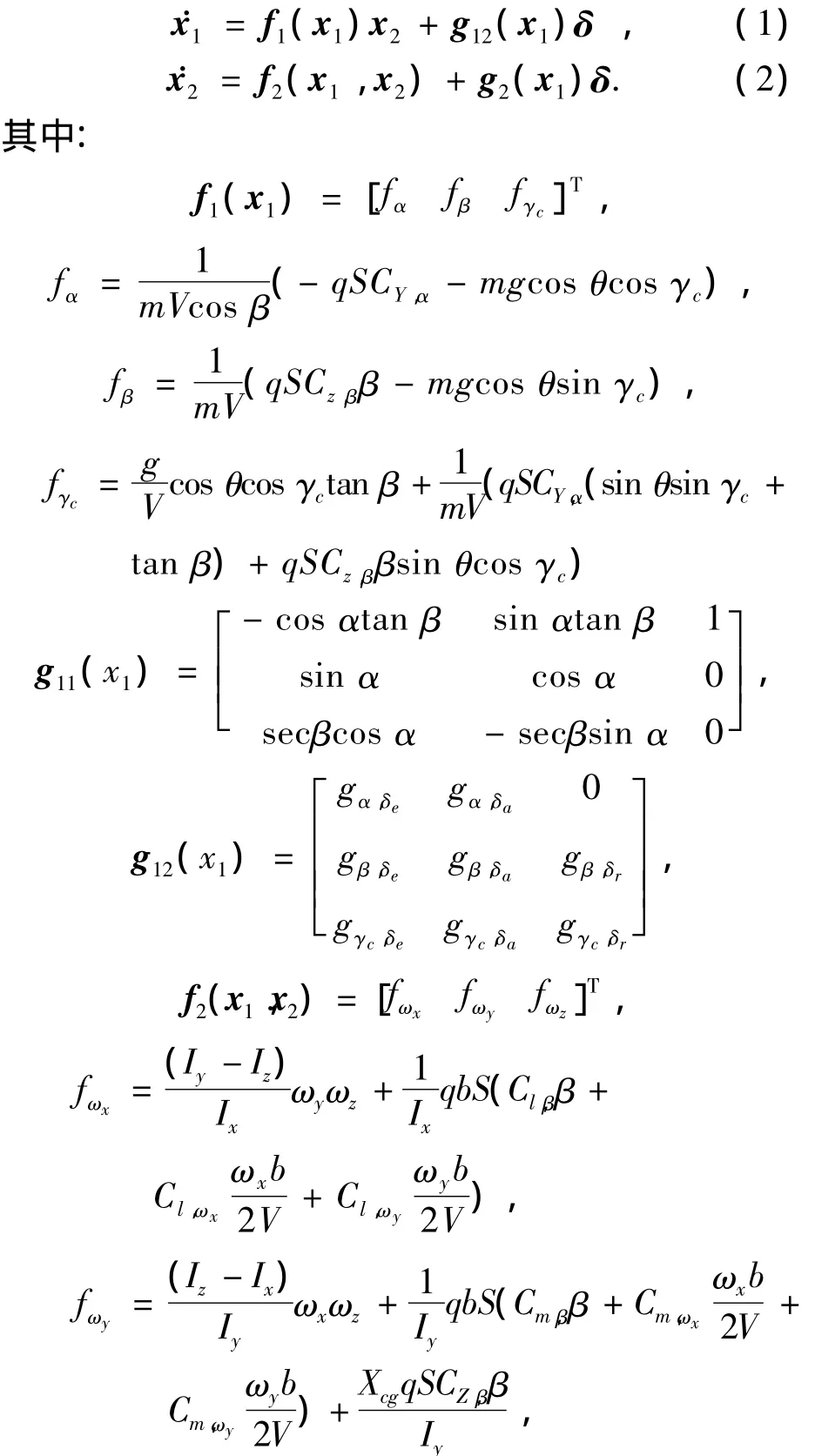
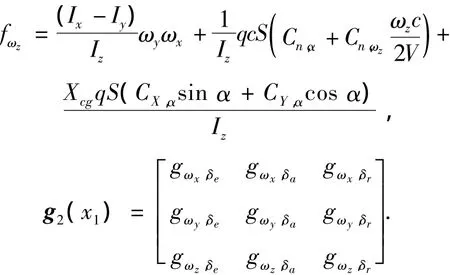
上述符号中gi，j为气动参数项，具体参数详见参考文献[13].与一般低速飞行器不同的是，各个气动参数项都是攻角和马赫数的函数，并且包含气动参数摄动引起的不确定性，增强了通道间的耦合，导致控制器设计更加复杂和困难.

2 连续光滑ESO构造

扩张状态观测器(ESO)是自抗扰控制理论中的关键技术，不仅能观测出对象状态，还能利用“扩张状态”实时估计出对象的不确定性和外部干扰总和.在进行ESO设计时，使用的han(e，a)函数如下:

为了避免高频颤振现象的出现，把函数|e|asign(e)改造成原点附近具有线性段的连续的幂次函数 fal(e，a，σ).

式中σ为线性段的区间长度.

但是han函数在原点处导数为无穷大，因此在原点附近将产生高频颤振现象.将其改造为fal(e，a，σ)后，虽然连续，但不可导(即不光滑).如果误差在线性段内变动，则消除了振荡影响，但是如果σ取值较小，导数的突变将导致系统性能变坏，并不能避免高频颤振，甚至产生更大的振荡，控制效果反而不如han函数，由于控制品质对σ的取值较敏感，在设计自抗扰控制器时，σ是需要调整的参数，增加了自抗扰控制器设计的难度.因此，将 fal(e，a，σ)函数改造为连续光滑函数(即 qin(e，a，σ)函数)，即将 fal函数中的线性段部分改造成连续光滑部分是解决此问题的关键.

在|e|＞σ区间内，qin函数满足

在|e|≤σ区间内，为满足函数在零点连续且取值为零，设

为满足连续光滑条件，则式(4)满足如下条件:

代入解得

因此，最后完整的qin(e，a，σ)函数形式如下:

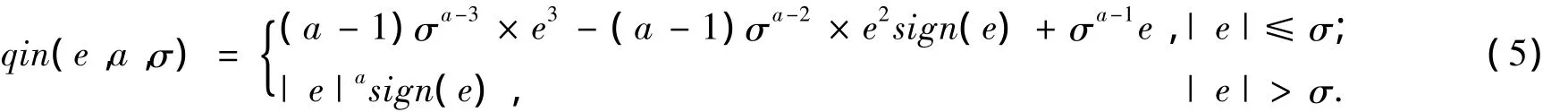
取a=0.25，σ =0.1，函数han(e，a)、fal(e，a，σ)及qin(e，a，σ)的图形如图1所示.

图1 函数输出图形

从图1可见，qin函数各点连续且光滑，避免了ESO的高频颤振现象，并且对σ的取值不敏感，一般取σ =10－5即可，下文ESO及NLSEF设计均是采用qin函数.

3 自抗扰姿态控制器设计

由于系统(1)需要考虑系统(2)的耦合，因此首先对系统(2)设计自抗扰控制器.

系统(2)的对象为弹体姿态动力学系统.每个通道均为一阶系统，因而只需重构二阶ESO.控制量x2的输入矩阵参数g2(x1)与气动参数相关，虽然有相关参数可参考，但是并不是精确值，故g2取参考的气动参数作为标称值g20.由于f2(x1，x2)也存在参数摄动及不确定项，因此用f2(·)代替，f2(·)为总的不确定项，包括 f2(x1，x2)及外部环境干扰、未建模动态、耦合影响等干扰.

用估计值 g20代替 g2，f2(·)代替 f2(x1，x2)，则方程(2)可等效为

其中:

对系统(6)的3个通道均配置相同结构相同参数的二阶ESO.推广的二阶MIMO ESO方程为

即ESO状态将分别实时估计出弹体角速度和模型中总不确定项a(t).为补偿“总和干扰”影响，利用估计值z22，对弹体姿态动力学系统(3)实施下列动态反馈补偿律:

则系统(3)被动态反馈线性化为单积分器系统

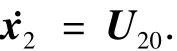
可见，采用ESO实现这种动态反馈补偿无需已知f2(·)和精确的参数值，允许带有参数摄动、不确定项和干扰影响，动态补偿后，从控制输入U20至输出x2之间的3个通道成为并行的3个单积分器系统，3个通道得到了解耦.

尽管ESO对系统总扰动有出色的估计能力，动态反馈补偿后，不可避免地仍存在补偿残差.为了快速抑制补偿残差，控制律采用具有非线性反馈效应的NLSEF，对积分系统进行控制:

式中b3＞0，0＜a3＜1，σ3为标量.

由式(6)可得飞行器操纵舵面的控制指令δ为

下面考虑系统(1)与系统(2)之间的耦合，对系统(1)设计自抗扰解耦控制器.

随着近几年我国对“三农”投入的不断加强，土地整治越来越体现出其在解决“三农”问题中的重要作用，受到各级政府的高度重视。《中共中央国务院关于加大统筹城乡发展力度进一步夯实农业农村发展基础的若干意见》(中发[2010]1号)明确提出了要有序开展农村土地整治。土地整治规划则是保障土地利用总体规划的目标任务全面落实的重要措施，是规范有序开展土地整治工作的重要依据。近年来,随着我国农用地整理项目和未利用地开发项目的实施，补充耕地的重点逐渐转向了农村居民点复垦[1]。因此，科学、合理地进行农村居民点复垦潜力估算以及分区研究是土地整治规划的重要环节，是规划方案拟定的基本依据。

将U1当作虚拟控制量，重构二阶ESO，其方程为

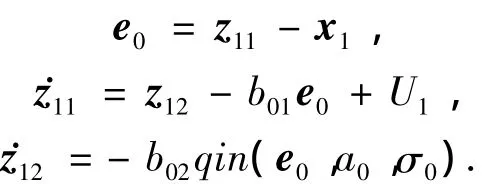
同理，只要ESO参数选择合适，满足二阶ESO的稳定性条件则稳态时，ESO状态将有下列收敛关系:

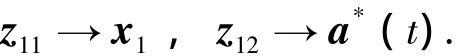
对系统(7)实施下列动态反馈补偿:

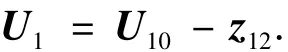
则系统(7)被动态反馈线性化为单积分器系统

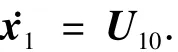
为实现高精度跟踪期望输入，外环仍选择NLSEF，即

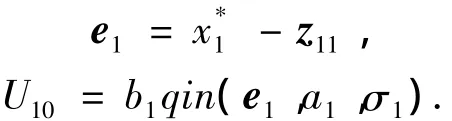
其中b1＞0，0 ＜a1＜1.

则由式(5)可得

从上述过程可以看出，自抗扰串级解耦姿态控制器的设计，无需精确的弹体姿态模型，只需输入估计值，几乎不依赖于弹体姿态模型.

4 仿真分析

以高超声速飞行器模型为例进行仿真，主要考察控制系统在气动参数大范围摄动情况下的性能，仿真中气动参数摄动范围为±50%.αd和γcd分别如图2～4中实线对应的制导指令信号所示，由飞行器的BTT控制协调要求直接令βd=0.

被控系统参数如下:

控制器仿真参数如下:

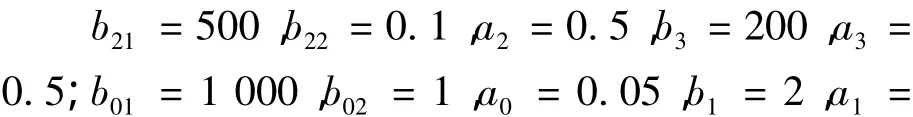
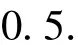
仿真结果如图2～4所示，图2为攻角响应曲线，图3为侧滑角响应曲线，图4为倾侧角响应曲线.其中，红虚线为文献中标准参数下的跟踪曲线，绿点线为气动参数摄动50%时的跟踪曲线，蓝点划线为气动参数摄动－50%时的跟踪曲线.

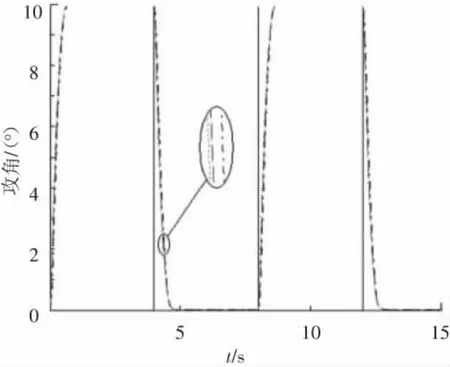
图2 攻角响应曲线

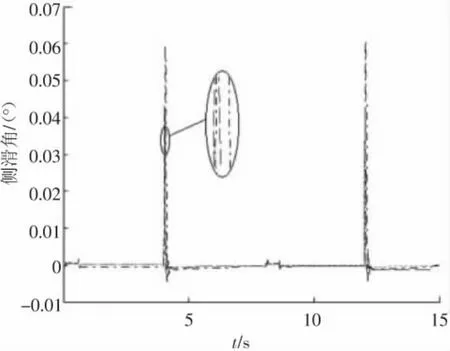
图3 侧滑角响应曲线

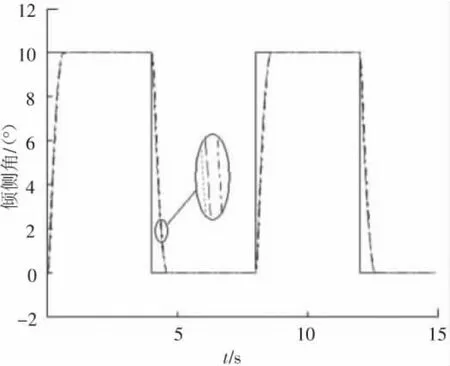
图4 倾侧角响应曲线

仿真结果表明，在标准参数情况下，攻角及倾侧角均能快速、无超调的跟踪制导指令信号，具有良好的动态品质和较高的跟踪精度，且侧滑角满足|β|≤0.1°.在气动参数大范围摄动的情况下，三通道也均能满足稳定性要求，控制系统仍表现出良好的跟踪性能，具有很强的鲁棒性.

5 结论

本文针对高超声速飞行器无动力再入的姿态非线性模型，通过连续光滑ESO构造及自抗扰串级耦合控制技术，设计了便于工程实际应用的高超声速飞行器自抗扰姿态控制器.仿真表明构造的qin函数可避免自抗扰控制器应用过程中的高频颤振现象，并且便于自抗扰控制参数调整.控制系统具有良好的动态品质和跟踪性能，能够克服气动参数大范围摄动的影响，具有较强的鲁棒性.改进自抗扰串级耦合姿态控制器的设计考虑了内外环的耦合影响，无需精确的飞行器被控模型，并且对于气动参数也只需标准值或是估计值，无需知道气动参数摄动的界限，克服了实际工程中难以建立精确被控模型并获取参数摄动范围的困难，具有工程应用价值.

[1]BOLENDER M A.An overview on dynamics and controls-modelling ofhypersonic vehicles[C]//2009 American Control Conference.New York:[s.n.]，2009:2507－2512.

[2]WANG Q，STENGEL R F.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance，Control and Dynamics，2000，23(4):577 －584.

[3]ITO D，WARD D，VALASEK J.Robust dynamic inversion controller design and analysis for the X-38[C]//AIAA Guidance，Navigation，and Control Conference.Montreal:[s.n .]，2001.

[4]XU H J，MIRMIRANI M，IOANNOU P A.Robust neural adaptive control of a hypersonic aircraft[C]//AIAA Guidance，Navigation，and Control conference and Exhibit.Austin，Texas:[s.n.]，2003.

[5]WALLNER E M，WELL K H.Nonlinear flight control design for the X-38 using CMAC neural networks[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit.Montreal，Canada:[s.n.]，2001.

[6]高道祥，孙增圻，罗熊，等.基于Backstepping的高超声速飞行器模糊自适应控制[J].控制理论与应用，2008，25(5):805 －810.

[7]XU H J，IOANNOU P A，MIRMIRANI M.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance，Control and Dynamics，2004，25(5):829－838.

[8]YANG Junchun，HU Jun，LV Xiaole.Design of Sliding Mode Tracking Control for Hypersonic Reentry Vehicles[C]//Proceedings of the 26th Chinese Control Conference.Zhangjiajie，Hunan:[s.n.]，2007.

[9]ZHOU Yanxia，WU Yuxiang，HU Yueming.Robust Backstepping Sliding Mode Control of a Class of Uncertain MIMO Nonlin-ear Systems[C]//2007 IEEE International Conference on Control and Automation.Guangzhou:[s.n.]，2007.

[10]韩京清.自抗扰控制器及其应用[J].控制与决策，1998，13(1):19 －23.

[11]朱承元，杨涤，翟坤.无陀螺大挠性多体卫星的自抗扰姿态控制[J].计算机仿真，2005，22(1):43－47.

[12]SU J B，QIU W B.Robotic Calibration-free Hand-eye Coordination Based on Auto Disturbances Rejection Controller[J].Acta Automatica Sinica，2003，29(2):162 －167.

[13]SHAUGHNESSY J D，PINCKNEY S Z，MCMINN J D.Hypersonic vehicle simulation model:winged-cone configuration[R].NASA TM-102610，1990.