超空泡射弹尾拍振动特性分析

张劲生，张嘉钟，曹 伟，魏英杰，于开平

(哈尔滨工业大学 航天学院，150001哈尔滨，zjn88@126.com)

水下航行体高速运动时(＞50 m/s)，航行体表面附近的水会发生空化相变，形成覆盖航行体大部分或全部表面的超空泡.形成超空泡之后，航行体将在气体中航行，从而极大地降低了所受的流体阻力[1].利用超空泡减阻，水下射弹可以实现超高速水下飞行.由于发射时射弹会受到扰动，当飞行速度处于300～900 m/s时，弹体将发生尾拍.即射弹在前进的同时，还绕着其前端摆动，使射弹的尾部与空泡壁面发生连续地碰撞和反弹，如图1所示[2].在尾拍航行阶段，过大的动应力响应会导致弹体结构失效，过大的弯曲变形可以使射弹运动时发生翻滚失稳[3]，因此研究超空泡射弹的尾拍振动特性具有重要意义.

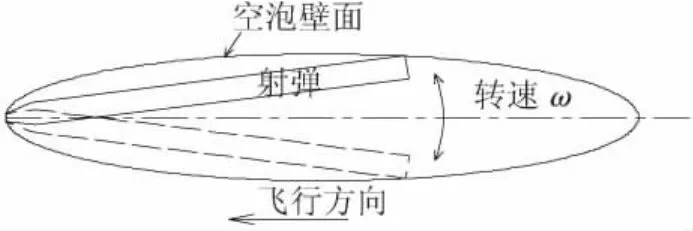
图1 射弹尾拍示意

尾拍过程中，射弹在绕头部转动的同时，弹体还发生振动.大范围的刚体转动与弹体变形运动发生相互耦合，使系统的振动特性与不考虑耦合效应时的系统振动有很大的不同，产生“动力刚化”现象.这时系统的振动频率和模态振型将是时变的，并随角速度而变化，而不是无刚体转动时系统振动的固有频率和固有模态[4].

到目前，国内、外对超空泡流的流体动力学特性已经进行了大量的研究，对超空泡航行体自身的力学特性也开始进行一些研究工作，主要是对超空泡鱼雷的振动特性和超空泡射弹的弹道、动力学的研究[5－9].但对超空泡射弹尾拍航行时的振动特性的研究还很少;尤其是考虑到射弹的刚体转动与振动发生了耦合作用，这时传统的结构动力学理论不再适用，应该采用刚－柔耦合动力学理论来研究系统的振动特性.

本文在前人关于刚－柔耦合动力学理论的基础上[4，10－11]，针对射弹尾拍运动的特点，建立其边界条件，得到了弹体横向振动的基频和一阶模态，并对它们与转速、长细比、弹体材料特性的关系进行了数值模拟和分析.本文得到的结果可以为进一步研究超空泡射弹的结构响应和进行优化设计提供必要的参考.

1 动力学控制方程及边界条件

为简化起见，可以将弹体模型简化为细长圆柱体，基于弹性梁变形理论和Hamilton变分原理，建立刚体转动与变形运动相互耦合的系统动力学方程.本文只考虑弹体的横向振动，不计其纵向振动，耦合动力学控制方程为[11]

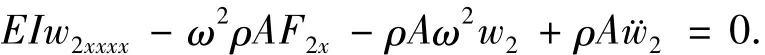
其中:F2=w2x[(x2－l2)/2－I/A];E为弹性模量;I为截面惯性矩;w2为弹体中线上点的横向位移;A为截面积;ω为转动角速度;ρ为密度;l为弹体长度;x为弹体轴向坐标.无量纲化后的方程为[11]

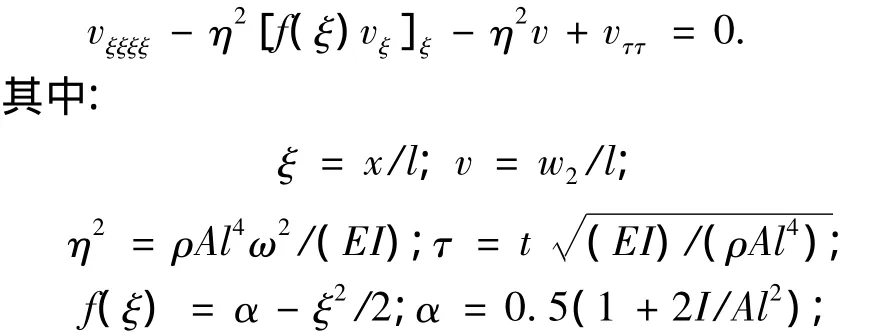
t为运动时间.

采用分离变量法求解控制方程，令

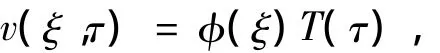
其中φ(ξ)为模态函数.对模态函数采用Frobenius法求解，则

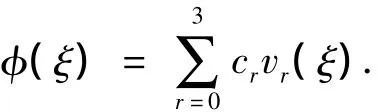
其中cr为待定系数，vr(ξ)可由递推关系求得.

在水阻力Fr、惯性力Fi、重力G和尾拍冲击载荷Fim的作用下，射弹在前进方向上作减速运动，同时弹体绕前端点o来回摆动，使尾部与空泡壁面不断发生碰撞并被反弹.为简化分析弹体的横向振动，可以将弹体近似看作是前端受简支约束，后端自由的梁，在外力作用下，以角速度ω做上下来回的摆动，如图2所示.

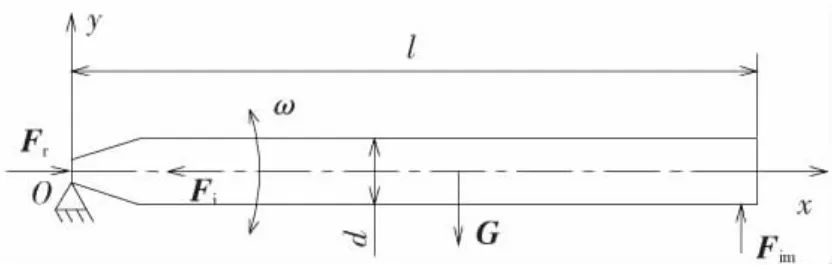
图2 射弹受力及约束

故可以建立无量纲化后的边界条件有:

拉丁美洲和加勒比海地区2017年的核电装机容量为5.1 GWe。该地区核电容量在2030年、2040年和2050年的高值情景预测值分别为10 GWe、17 GWe和20 GWe，低值情景预测值分别为8 GWe、7 GWe和8 GWe。

简支端

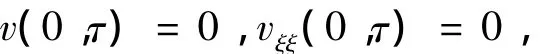
自由端

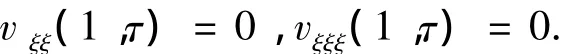
2 弹体基频和一阶模态

由简支边界条件可得c0=c2=0，所以

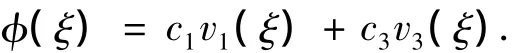
由自由端边界条件可得

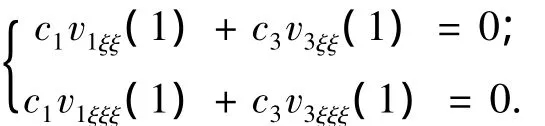
方程要有非零解，则必须

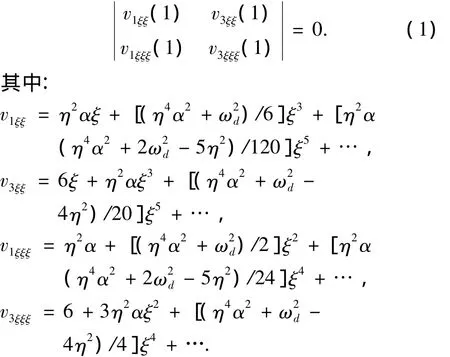
当 v1ξξ、v3ξξ精确到 ξ5、v1ξξξ、v3ξξξ精确到 ξ4时，由式(1)可得系统横向振动的频率方程为

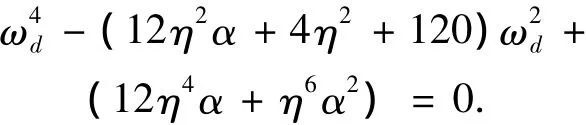
可解得系统一阶频率ωd(无量纲化值)为

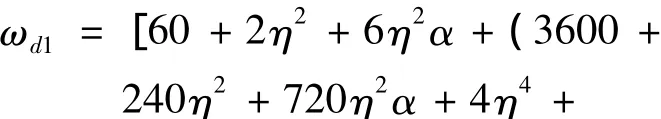
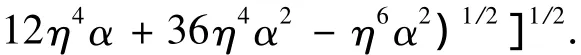
其中c3为任意常数.

3 数值模拟及分析

3.1 系统基频的计算和分析

为了分析弹体长细比和转速对横向振动频率的影响，取材料为钢，直径d=0.01 m，但长细比b=l/d不相同的系列射弹，利用前述的结果，分别对其一阶频率进行计算.当不考虑弹体转动与横向振动的耦合效应时，算得弹体横向振动的基频值，无量纲化后近似为11.当考虑转动角速度ω对系统频率的耦合影响时，可以得到如图3所示的横向振动基频图.

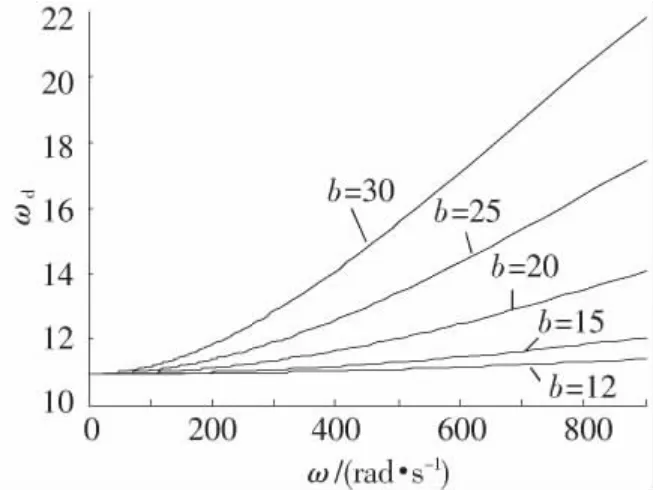
图3 不同长细比时，基频与转速关系

从图中可见，振动系统不存在所谓的固有频率，其频率值随转动角速度的增加而变大.同时，弹体长细比增大，使系统柔度增加，导致大范围转动对振动特性的影响更加显著，从而使振动频率随角速度的变化更迅速.当转速较小时(ω ＜50 rad/s)，或者长细比较小时(b＜12)，转动对振动频率的影响很小，可以认为系统的频率保持不变，等于不计耦合作用的影响时系统的固有频率.

为了分析材料特性对振动频率的影响，分别选取 h= ρ/E=3 × 10－8、3.4 × 10－8、3.9 × 10－8、4.2 ×10－8、6.5 ×10－8的材料进行计算，得到如图4所示的振动基频图.

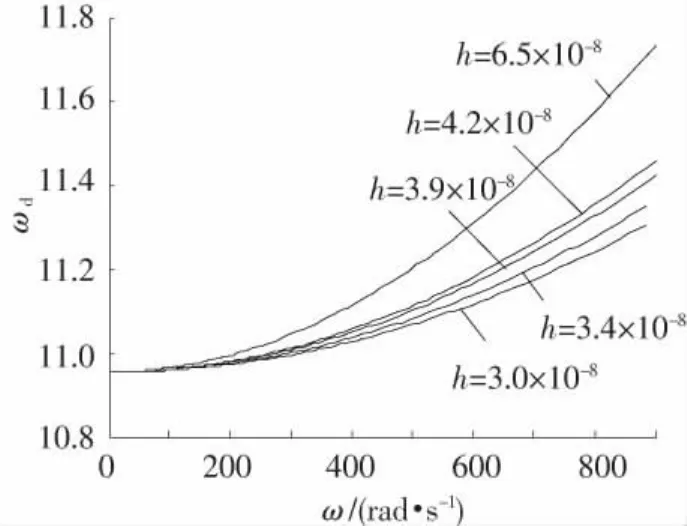
图4 不同材料下，基频与转速关系

可见h越大时，基频随着角速度增加得越明显.当转速较小时(ω ＜50 rad/s)，各种材料模型的频率都近似相同，这时可以认为基频与材料参数无关，也不随转速变化，并近似等于系统的固有频率.

3.2 系统一阶模态的计算和分析

对材料相同，但长细比b不同的射弹，在不同角速度下，计算弹体的一阶模态.可得到如图5、6所示的弹体一阶振型.再对长细比相同而材料特性量h不同的射弹，计算其一阶模态.得到如图7、8所示的弹体一阶振型.

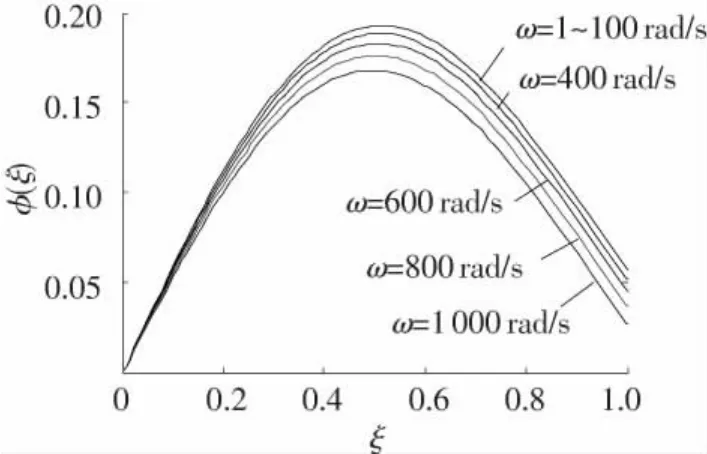
图5 b=12时，一阶模态与转速的关系

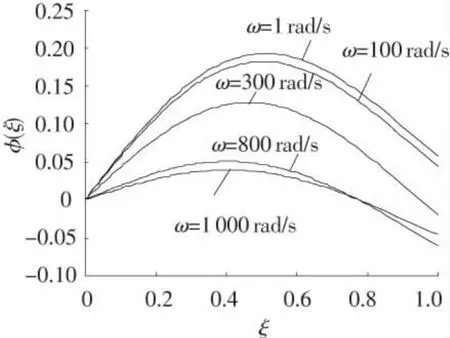
图6 b=30时，一阶模态与转速的关系

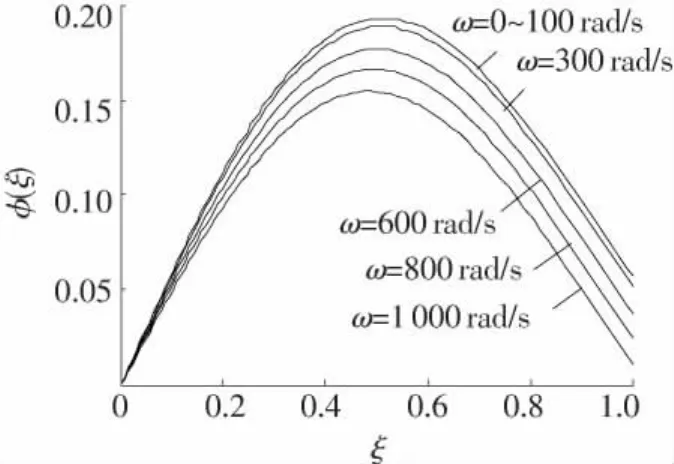
图7 h=6.5×10－8时，一阶模态与转速的关系

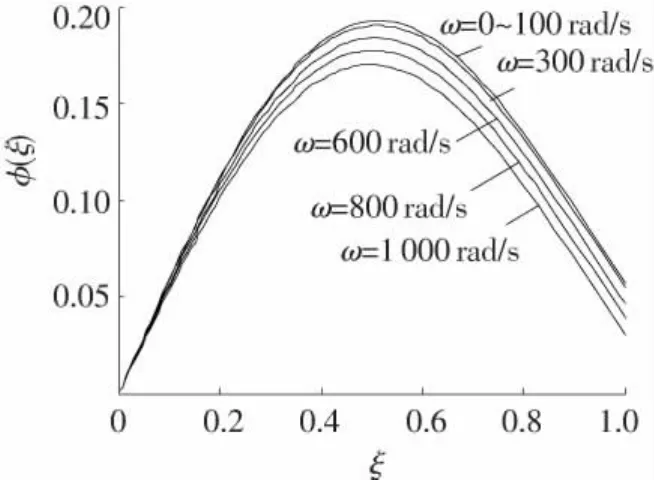
图8 h=3×10－8时，一阶模态与转速的关系

从图中可见，模态振型都随角速度的不同发生变化;比较图5和图6可以看出，当长细比b较大时，模态随角速度的变化更剧烈，转动与振动间的耦合效应更强烈.

同样，比较图7和图8，可见当弹体材料参数h=ρ/E较大时，模态随角速度的变化更显著.

但当转速ω＜100 rad/s时，可近似地认为弹体模态是不变的，不受转速、长细比和材料的影响，并与不计转动的耦合影响时系统的固有模态相同.

可见，弹体越细长，刚度越小，转动角速度越大，都会使弹体的大范围转动对弹体振动的耦合作用增强，使模态出现明显的变化.但当转速较小时(ω＜100 rad/s)，可忽略耦合作用的影响，并认为系统模态是不变的，等于其固有模态.

4 结论

1)弹体长细比的增大和材料常数h的增加，会使弹体的整体刚性降低，这将使大范围转动对弹体振动的耦合作用增强，从而导致振动频率和模态随转速的变化更加显著.

2)当长细比较小时(b＜12)，弹体转动对振动频率的影响可忽略不计，认为振动频率等于不考虑转动影响时系统的固有频率.

3)较小的转速下，可以忽略耦合作用对振动的影响;当角速度ω＜50 rad/s，可采用系统的固有频率值，当ω ＜100 rad/s，可采用弹体的固有模态.

[1]ANUKUL G.Robust control of supercavitating vehicles in the presence of a dynamic and uncertain cavity[D].Florida:University of Florida，2005.

[2]SAVCHENKO Y N.Control of supercavitation flow and stability of supercavitating motion of bodies[C]//RTO AVT lecture series on supercavitating flows.Brussels Belgium:[s.n.]，2001.

[3]HRUBES J D.High-speed imaging of supercavitating underwater projectiles [J]. Experiments in Fluids，2001，30:57 －64.

[4]蒋丽忠，周凌宇，罗小勇.刚一柔耦合系统动力学分析[J].长沙铁道学院学报，2000，18(3):1－5.

[5]杨传武，王安稳.动态轴向载荷对超空泡航行体振动特性的影响[J].华中科技大学学报，2008，36(12):71－74.

[6]RAND R，PRATAP R，RAMANI D.Impact dynamics of a supercavitating underwater projectile[C]//Proceedings of the 1997 ASME Design Engineering Technical Conference.Sacramento:ASME，1997.

[7]KULKARNI S S，PRATAP R.Studies on the dynamics of a supercavitating projectile[J].Applied Mathematical Modelling，2000(24):113－129.

[8]孟庆昌，张志宏，顾建农，等.超空泡射弹尾拍分析与计算[J].爆炸与冲击，2009，29(1):56－60.

[9]曹伟，魏英杰，韩万金，等.超空泡航行体阻力系数的数值模拟研究[J].工程力学2008，25(12):208－212.

[10]YOO H H，SHIN S H.Vibration analysis of rotating cantilever beams[J].Journal of Sound and Vibration，1998，212(5):807－828.

[11]蒋丽忠，洪嘉振.大范围运动对弹性梁振动频率及模态的影响[J].振动与冲击，1999，18(1):13－16.