基于波束成形的MIMO-OFDM插值算法

何春龙 尤肖虎 朱鹏程 盛 彬

(东南大学移动通信国家重点实验室，南京 210096)

多径衰落和频谱效率是未来移动通信系统中的2个最主要挑战.正交频分复用(orthogonal frequency division multiplexing，OFDM)技术将信道分成若干个并行子信道，能够将频率选择性信道转变为平坦衰落信道，而多输入多输出(multiple input multiple output，MIMO)技术可显著提高平坦衰落信道的容量，从而大幅度提高频谱效率.因此，将MIMO和OFDM技术相结合可实现数据在无线通信系统中的高速传输［1-2］.

已有的研究成果表明，MIMO-OFDM技术在发射端已知信道状态信息(CSI)的前提下能显著提高系统性能［3-6］.单用户MIMO-OFDM 系统在发射端已知CSI时，可通过简单的波束成形或预编码技术来获得发射分集增益和阵列增益.在时分双工系统中可以利用信道的互易性得到发送端的CSI，而频分双工系统不具有互易性.因此在实际系统设计中，接收端通过有限反馈将某些与信道相关的信息发送给发射端.在MIMO-OFDM系统中，有限反馈数量与子载波个数成正比，因此即使采用量化的波束成形，反馈开销依然很大.针对MIMO-OFDM系统中反馈开销过大的问题，文献［7］提出了分组和线性球状插值算法，接收端只需反馈导频点的波束成形向量，非导频点的波束成形向量通过子载波频率的相关性得到;文献［8］通过在Grassmann流形上求解最小二乘法得到非导频子载波上的波束成形向量从而减少反馈开销;文献［9］提出了三阶样条补插和变换域补插的方法来减少反馈开销;文献［10-12］针对多用户MIMO-OFDM系统提出利用子载波频率之间的相关性来减少反馈开销.本文针对线性球状插值算法复杂度过大并且只适用于非量化波束成形的情况，提出了一种通用的插值算法，并在通用插值算法基础上提出了一种相位量化方法.

1 系统模型

图1所示为Mt根发送天线、Mr根接收天线、N个子载波的MIMO-OFDM系统.在发送端，调制信号{S(k)，k=1，2，…，N}首先乘以对应的波束成形向量 w(k)={w1(k)，w2(k)，…，wMt(k)}T，然后经过IDFT变换后，信号通过频率选择性衰落信道发送出去.假设H(k)为Mr×Mt信道矩阵，其中的元素表示第k个子载波的复信道增益.接收端经过 z(k)={z1(k)，z2(k)，…，zMr(k)}T向量合并后，第k个子载波信号可表示为

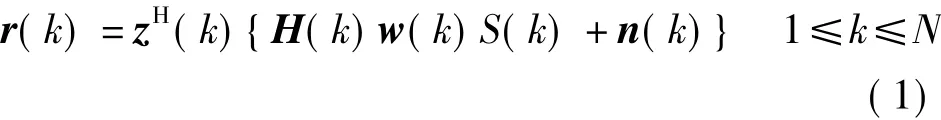
式中，n(k)是均值为0，方差为N0的Mr维独立同分布复高斯噪声.假设信道参数仅在接收端已知，且子载波功率满足，则第 k 个子载波的信噪比(SNR)可表示为［7］

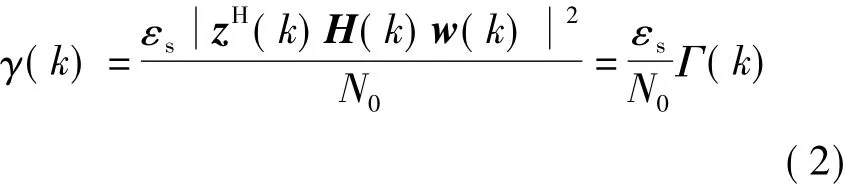
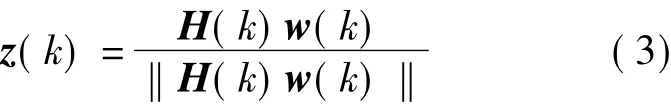
图1 Mt发Mr收MIMO-OFDM波束成形有限反馈系统框图

2 MIMO－OFDM波束成形插值算法

在MIMO-OFDM波束成形系统中，波束成形向量在频域上具有相关性，因此可利用该特性来减少波束成形向量反馈量，即只反馈子载波上的波束成形向量，然后利用信道频域相关性，内插重构非导频子载波上的波束成形向量.因此，关键问题是利用性能好的插值算法来重构非导频子载波上的波束成形向量.下面将具体介绍各种插值算法.

2.1 线性球状插值算法

为了表示方便，记wl=w(lK+1)，0≤l≤N/K－1，则第lK+k个子载波的线性球状插值计算公式为［7］

式中，K为一组子载波的大小;ck=(k－l)/K为线性权重值;wN/K=wN/K－1;θl为相位旋转参数.为了得到线性插值的最佳性能，接收端需要计算出最优的相位值.如果以平均误码率性能最小为准则优化相位值，那么相位参数的代价函数非常复杂.文献［7］提出了将一组子载波中有效信道增益的最小值最大化的准则，得到次优的相位参数为

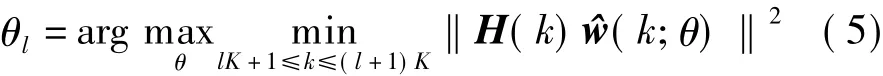
通过假设第lK+K/2+1个子载波有最差的有效信道增益，相位旋转参数θl可表示为［7］

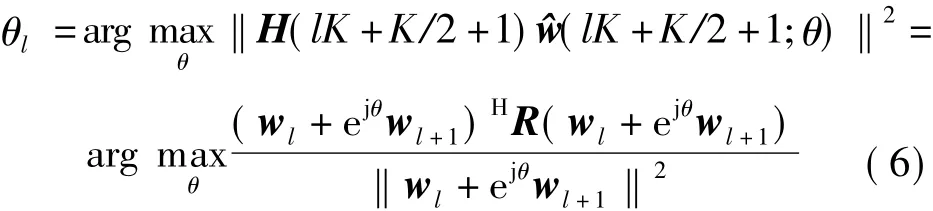
式中，R=HH(lK+K/2+1)H(lK+K/2+1).经数学推导，式(6)的解可表示为［7］

其中

2.2 提出的通用插值算法

通过分析2.1节的线性球状插值算法，可发现式(6)的闭式解有2个问题:①算法求解过程非常复杂;②不适用于量化波束成形的情形.比如当使用的码书长度为16，子载波个数为64，则这64个子载波波束成形向量是由长度为16的码书组成的，因此必然存在2个或以上子载波的波束成形向量相同，故η1=0，因此式(7)没有解.针对这2个问题，本文提出了一种通用的插值算法，该方法不仅适用于非量化波束成形，并且也适用于量化波束成形.其数学表达式为

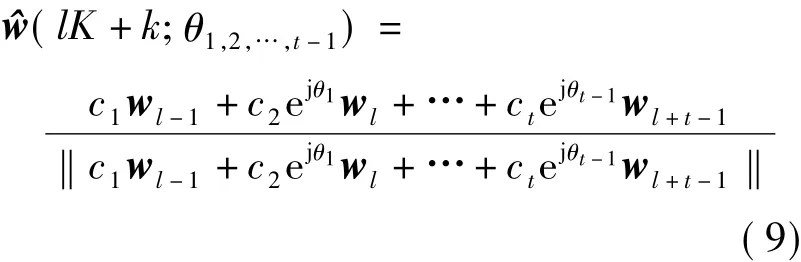
式中，c1，c2，…，ct为权重值;w－1=w0;wN/K=wN/K－1，0≤k≤K;θ1，θ2，…，θt－1为相位旋转参数.令x=c1wl－1+c2ejθ1wl+ … +ctejθt－1wl+t－1，则次优的相位旋转参数 θ1，2，…，t－1可表示为

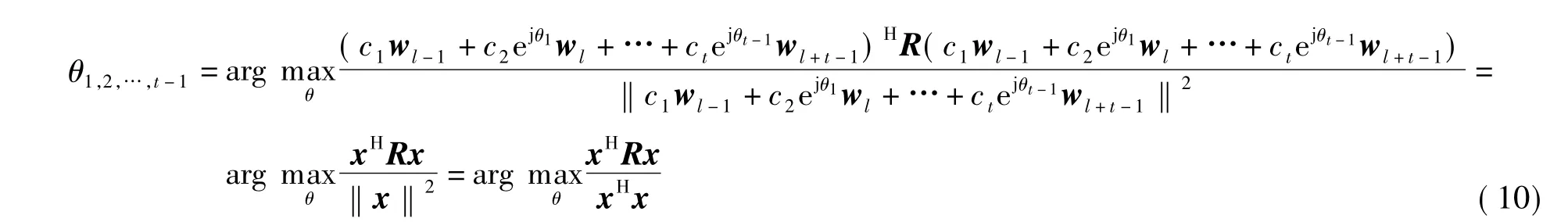
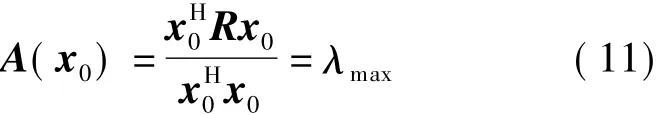
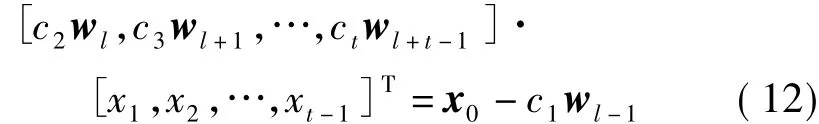
式(12)的解为

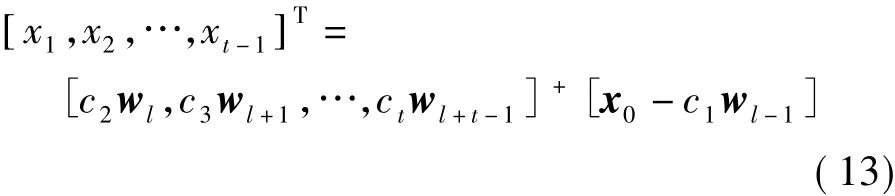
式中，［］+表示伪逆.从式(10)的解可得出相位旋转参数一定要小于等于发射天线个数.该限制条件对式(13)在实际应用中没有影响，因为相位旋转参数一旦大于天线个数，那么实际的系统将极大地增加反馈量.通过应用Rayleigh熵定理，可得到简化的通用插值算法为

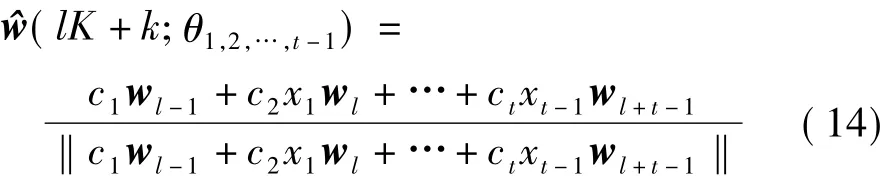
2.3 二阶高斯插补算法

二阶高斯插补算法是利用前后3个连续的导频子载波波束成形向量估计非导频子载波波束成形向量.则第lK+k个子载波的二阶高斯插补算法计算公式为［9］

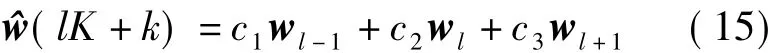
其中

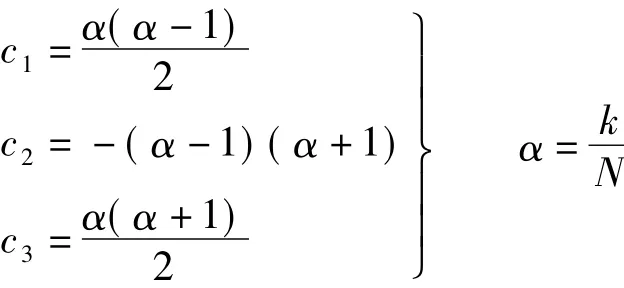
2.4 变换域插补算法

首先将反馈得到的波束利用IDFT将其变换到变换域，即［9］

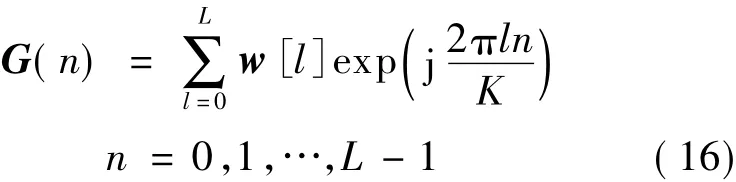
其中，L=N/K.保留G(n)序列中前L0个点的值不变，后L－L0个点的值置0，即

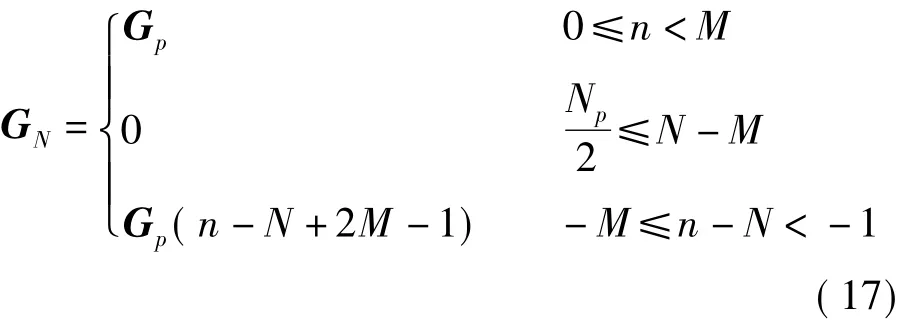
其中，M=K/2+1.设得到的新序列为 G′(n)，将G′(n)进行 DFT 变换得［9］

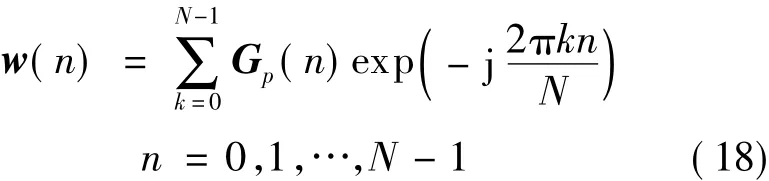
2.5 提出的相位量化法

由式(13)可看出相位旋转参数无法量化，因此本文提出一种新的量化方法，即通过选择相位旋转参数使一组子载波中总的有效信道增益最大化.下面以二阶插值为例来说明量化过程.经过修正的高斯插值算法数学表达式为

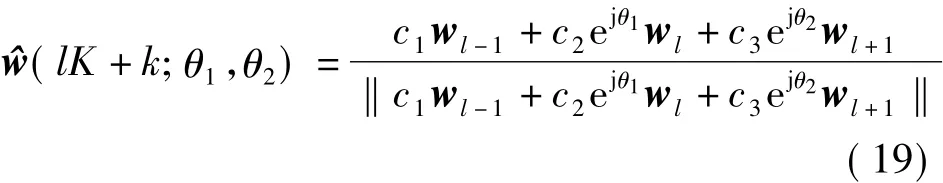
则次优的相位旋转参数可表示为

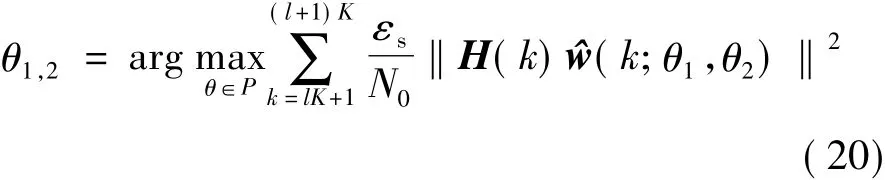
式中，P={0，2π/T，4π/T，…，2(L －1)π/T}，T 为相位旋转参数量化级别，决定了系统性能和复杂度.T越大，系统性能越好，但算法复杂度和反馈量都相应地增加.因此实际系统中应选择合适的T值.

3 计算复杂度与反馈开销分析

考虑到实际系统的可实现性，对各种插值算法的反馈量都在量化波束成形情况下进行比较.波束成形向量采用码书W进行量化，每个波束成形向量需要反馈量，因此理想的量化波束成形需要的反馈量，分组方法、二阶高斯插补和变换域插补的反馈量都为，线性球状插值算法波束成形向量反馈量为，同时相位参数需要的反馈量为N/Klog2T.为了便于比较，本文提出的通用插值算法和相位量化法都仅采用一个相位参数，因此其反馈量与线性球状插值算法相同.各种插值算法的反馈量如表1所示.

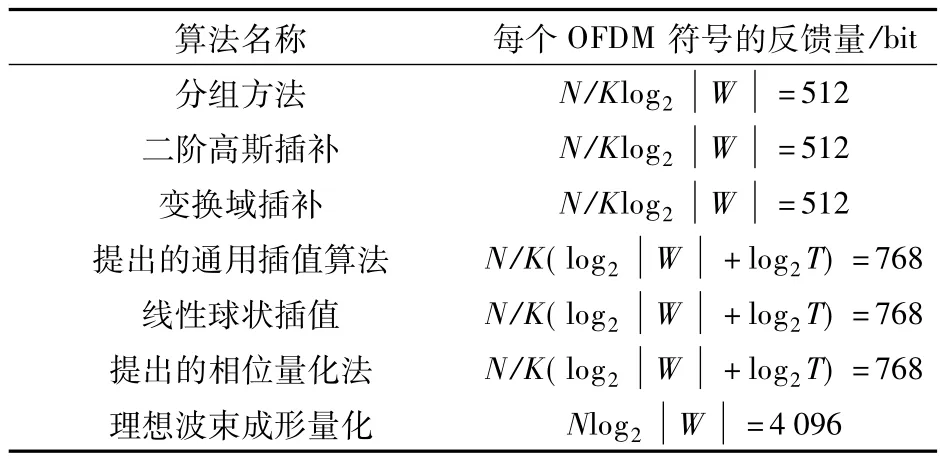
表1 各种插值算法反馈量比较(N=1024，K=8，T=4，W=16)

本文中计算复杂度定义为每个OFDM符号需要的复数乘法次数，因为同步、信道估计、QAM调制与解调、接收端合并和DFT/IDFT对各种算法复杂度都一样，因此本文不考虑它们的复数乘法，仅考虑插值算法、波束成形量化和相位量化的复杂度.分组方法的量化复杂度为K，二阶高斯插补时式(15)产生的复杂度为3NMt，变换域插补时式(16)和(18)产生的复杂度分别为N/2log2N和N/2log2N/K，线性球状插值时式(4)产生的复杂度为2NMt，提出的相位量化法由式(20)产生的复杂度为NT.具体比较如表2所示.

表2 各种插值算法复杂度比较(N=1024，K=8，T=4，W=16)

4 仿真结果

MIMO-OFDM系统仿真参数设置如下:发射天线数Mt=4，接收天线数 Mr=2;载频fc=3.5 GHz，带宽B=20 MHz，OFDM 采用N=1 024个子载波，循环前缀长度为256个样点;仿真信道采用室外环境［13］，其功率延时谱服从负指数衰落，最大多径时延为7 μs;采用QPSK调制，每条时域多径均采用瑞利衰落信道，且不同的收发天线之间的信道是独立同分布的，信道在一帧内不变.本文考虑非量化波束成形和量化波束成形2种情况，在量化波束成形中码书长度W=16，即每个波束成形向量只需反馈4 bit信息给发送端［14］.为了比较的公平性，本文提出的通用插值算法和相位量化法都只采用一个相位参数，并且在通用插值算法中2个加权系数为［15］

图2和图3分别为非量化和量化波束成形向量情形下的插值算法误比特率(BER)性能比较曲线图，其中Choi等［7］提出的插值法指的是式(6)的解.由图2和图3可看出，本文提出的通用插值算法在非量化和量化波束成形向量情形下误比特率性能明显优于分组方法、二阶高斯插补和变换域插补.在BER为1.0×10－3时，提出的通用插值算法在非量化和量化情形下相对分组方法分别有2.5和5 dB的信噪比增益，由此可证明本文提出的通用插值算法的正确性.同时也可看出，本文提出的相位量化方法在非量化和量化波束成形向量情形下误比特率性能都接近理想波束成形性能.在BER为1.0×10－3时，提出的相位量化方法在非量化和量化情形下相对通用插值算法分别有1和2 dB的信噪比增益;Choi等［7］提出的插值法在非量化波束成形下也具有好的性能，但本文提出的通用插值算法和Choi等［7］提出的插值法都没有量化相位，因此在实际系统中不能实现.

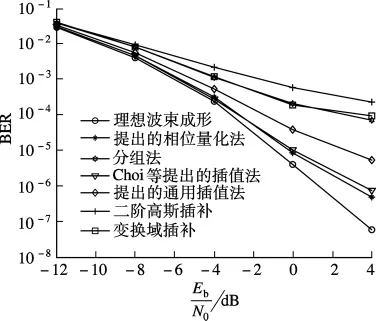
图2 非量化波束成形下的插值算法BER性能比较

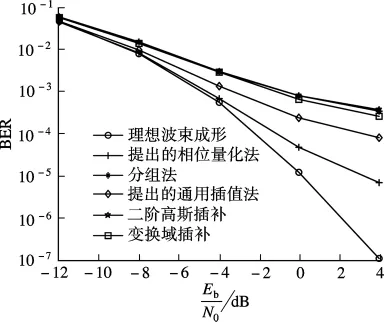
图3 量化波束成形下的插值算法BER性能比较

由表1可看出，二阶高斯插补、变换域插补以及分组方法所需的反馈开销最小，提出的通用插值算法和相位量化方法的反馈量和Choi提出的插值法相当，相对分组方法增加了50%，相对理想波束成形量化减少了81.25%.由表2可看出，分组方法算法复杂度最低.本文提出的相位量化方法、通用的插值法和Choi提出的插值法在反馈开销和复杂度方面大体相当;通用的插值算法复杂度相对分组方法增加了16.7%，相对理想波束成形量化减少了85.4%.

综上所述，如果系统对误比特率性能要求不是很高，而对复杂度和反馈量有较高要求，则分组方法是最好的选择;如果系统对误比特率要求高，对反馈量和复杂度没有过高要求，并且要求能实际实现(即波束成形向量和相位参数都要求量化)，则本文提出的相位量化法将是很好的选择.

5 结语

为了减少MIMO-OFDM系统中波束成形向量的反馈开销，本文提出了一种通用的插值算法和相位量化方法.通用的插值算法结构简单，但因为反馈相位没有量化，因此在实际系统中不能实现.而相位量化方法反馈的导频波束成形向量和相位信息都已经量化，因此便于实际系统实现.仿真结果表明，提出的相位量化方法的误比特率性能优于现有的插值算法，并且易于实际系统实现.

References)

［1］ Sampath H，Talwar S，Tellado J，et al.A fourth-gener-ation MIMO-OFDM broadband wireless system:design，performance and field trail results［J］.IEEE Commun Mag，2002，40(9):143-149.

［2］ Yang H W.A road to future broadband wireless access:MIMO-OFDM-based air interface［J］.IEEE Commun Mag，2005，43(1):53-60.

［3］ Ghaderipoor A，Tellambura C.Minimum distancebased limited-feedback precoder for MIMO spatial multiplexing systems［C］//IEEE Vehicular Technology Conference.Montreal，Canada，2006:416-419.

［4］Zhou S，Giannakis G.Optimal transmitter eigen-beamforming and space-time block coding based on channel mean feedback［J］.IEEE Trans Signal Process，2002，50(10):2599-2613.

［5］ Mukkavilli K K，Sabharwal A，Erkip E，et al.On beamforming with finite rate feedback in multiple-antenna systems［J］.IEEE Trans Inf Theory，2003，49(10):2562-2579.

［6］ Love D J，Heath R W，Santipach W，et al.What is the value of limited feedback for MIMO channels? ［J］.IEEE Commun Mag，2004，42(10):54-59.

［7］ Choi J，Heath R W.Interpolation based transmit beamforming for MIMO-OFDM with limited feedback［J］.IEEE Trans Signal Process，2005，53(11):4125-4135.

［8］ Pande T，Love D J，Krogmeier J V.Reduced feedback MIMO-OFDM precoding and antenna selection［J］.IEEE Trans Signal Process，2007，55(5):2284-2293.

［9］邹应全，李春国，杨绿溪.MIMO-OFDM系统中反馈插值方法和复杂度［J］.东南大学学报:自然科学版，2010，40(5):885-889.Zou Yingquan，Li Chunguo，Yang Lüxi.Interpolation of beamforming in the reduced feedback of MIMOOFDM systems［J］.Journal of Southeast University:Natural Science Edition，2010，40(5):885-889.(in Chinese)

［10］ Fakhereddin M，Sharif M，Hassibi B.Reduced feedback and random beamforming for OFDM MIMO broadcast channels［J］.IEEE Trans Commun，2009，57(12):3827-3835.

［11］ Shirani-Mehr H，Caire G.Channel state feedback schemes for multiuser MIMO-OFDM downlink［J］.IEEE Trans Commun，2009，57(9):2713-2723.

［12］ Sánchez-García J，Soriano-Equigua L，Heath R W Jr.Quantized antenna combining for multiuser MIMOOFDM with limited feedback［J］.IEEE Signal Process Letters，2010，16(12):1027-1031.

［13］ Horn R A，Johnson C R.Matrix analysis［M］.New York:Cambridge Press，1985.

［14］ European Telecommunications Sdandards Institute.ETSI TS 101 475 Broadband radio access networks;HIPERLAN type 2;physical(PHY)layer［S］.Sophia Antipolis Cedex，France:ETSI，2000.

［15］He C L，Peng Z M，Zeng Q.A novel OFDM interpolation algorithm based on comb-type pilot［C］//IEEE WirelessCommunications，NetworkingandMobile Computing Conference.Beijing，China，2009:893-896.