基于EEMD的奇异谱熵在旋转机械故障诊断中的应用

高清清 贾民平

(东南大学机械工程学院，南京 211189)

机械设备中大部分都是旋转机械，旋转机械设备发生异常或故障时，其振动信号多表现为非线性、非平稳特征［1］.对于这类非平稳信号的分析方法有短时傅里叶变换、Wigner-Ville分布、小波变换［2］等，但这些方法都存在一定的局限性.如短时傅里叶变换自适应性差;Wigner-Ville分布存在交叉干扰项;小波变换需预先设定基函数和分解尺度，难以在工程中得到广泛使用.

经验模式分解(EMD)［3］是将信号分解为有限个高频到低频的本征模态函数(IMF)的和.由于该方法的自适应性，在处理非线性、非平稳信号上具有明显的优势，因此，近年来被广泛应用于机械故障诊断［4-5］.但 EMD存在模态混叠问题，模态混叠［6］是指1个IMF分量中包含差异很大的特征时间尺度，或者相近的特征时间尺度分布在不同的IMF分量中，为了抑制模式混叠，Huang等［7］提出集合经验模式分解(EEMD)，是一种噪声辅助的数据分析方法，能够很好地还原信号的本质，是对EMD算法的重大改进.

另一方面，奇异谱熵在机械信号信息量评估、信息成分分析等多方面有独特性能，是对时间序列进行空间的一个重构.但奇异谱熵需人为确定嵌入维数和延时常数，限制了其在机械故障诊断中的应用［8］.本文提出基于EEMD的奇异谱熵的故障诊断方法，以车削细长轴为试验对象，采集车削时的振动信号，利用该方法对其进行分析.

1 EMD算法和EEMD算法

设原始信号为x(t)，EMD算法是把x(t)分解为一组IMF分量ci和余项rn的和，即

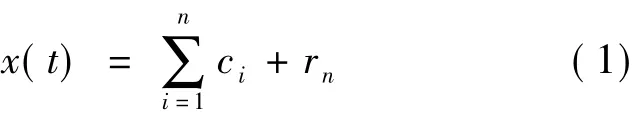
EMD存在的模式混叠使得IMF分量的物理意义不清楚，错误地显示了信号的时频分布.Huang等［9］认为模式混叠是信号的间歇现象，与极值点的选择有关.

EEMD算法的实质是在原始信号上叠加高斯白噪声，进行多次EMD分解，取IMF分量的均值作为最终结果.该算法利用高斯白噪声的统计特性，使得加入噪声后的信号在不同频率尺度上具有连续性，有效解决了模式混叠问题.

EEMD算法过程如下:

①初始化EMD执行总次数M和白噪声的幅值系数 k，m=1.

②执行第m次EMD分解.

a)在原始信号x(t)上加一幅值系数为k的随机高斯白噪声 nm(t)，得到加噪的待处理信号xm(t)，即

b)用EMD分解xm(t)，得到p个IMF分量cj，m(j=1，2，…，p)，cj，m表示第 m 次试验分解出的第j个IMF;

c)当m＜M，m=m+1，返回步骤②.

③对M次分解的每个IMF计算均值，即

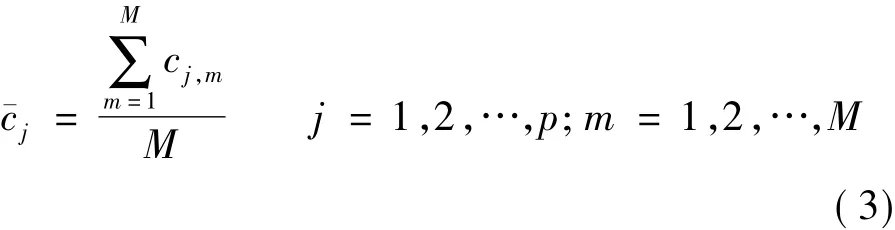
④输出¯cj作为EEMD分解得到的第j个IMF，j=1，2，…，p.

2 基于EEMD的奇异谱熵

信息熵的定义为［10］:假设A是一个可测集合类H生成的σ代数和具有μ测度，μ(A)=1的勒贝格空间，且可表示为有限划分A={Ai}中互不相容集合的形式，即则对于该划分A的信息熵为

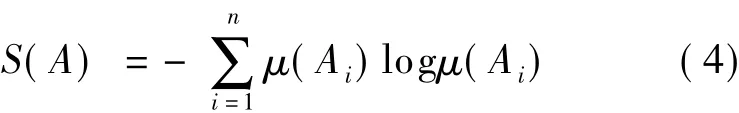
式中，Ai为划分模式;μ(Ai)为Ai的测度.

信息熵是对系统未知程度的一种度量.从信息熵的定义可看出，信号越复杂，即信号的模式越多，信息熵也越大.

由EEMD算法的原理可知，EEMD对x(t)进行分解，可得到p阶IMF分量和一个残余量rn，IMF分量分别表示了原始信号的不同频率特征，包含了不同的故障信息，因此根据不同的频率段将p阶IMF分量组成一个模式矩阵R，表示为

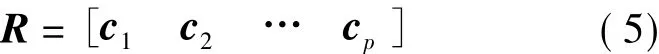
对模式矩阵R进行奇异值分解.假设获得的奇异值 μ1≥μ2≥…≥μM，则{μi}构成了原始信号的奇异值谱，是对信号在时域中的一种划分.若k为非零奇异值的个数，则k值反映了矩阵R的各列中包含的不同模式的数目.由此可以定义时域中信号的奇异谱熵为

3 仿真及应用实例

3.1 仿真试验

仿真信号x(t)由频率为20 Hz的正弦波x1和高频瞬态振荡信号x2组成，采样频率为2 kHz，采样点数为500，如图1所示.

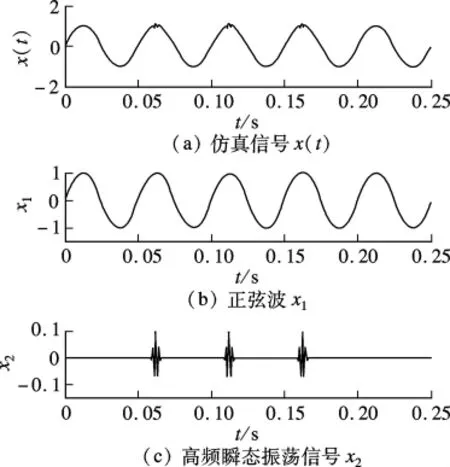
图1 仿真信号及其组成信号

对x(t)进行EEMD分解，白噪声的系数k=0.25，执行EMD总次数M=100，得到如图2所示的各阶IMF分量.从图2看出，第1阶分量c1与瞬态高频信号x2很相似，表明EEMD能将异常事件从原始信号中区别出来，而c1中幅值极小的波形是高斯白噪声的极少残留量.c4接近于信号x1，但其幅值略小于x1的幅值，c4与c5叠加后更接近x(t)中正弦波成分.可见，EEMD能高质量地分离出仿真信号中各个组成部分，没有发生模式混叠，真实、准确地反映出了信号的物理本质.

图2 仿真信号EEMD分解结果

根据奇异谱熵的理论分别求取原始信号x(t)和正弦信号x1的奇异谱熵值.x(t)和x1的熵值分别为0.516 44，0.343 64.x(t)的熵值较大是因为x(t)中混入了高频瞬态信号，频率成分丰富，模式复杂，而x1频率单一，故熵值较小，验证了基于EEMD的奇异谱熵方法的可行性.

3.2 切削加工工况分析

采用车削细长轴的振动信号，利用基于EEMD的奇异谱熵对发生颤振时的振动信号进行故障诊断.CK6140数控车床以恒定主轴转速1 000 r/min切削工件，采样频率2 kHz，采样点数6 000，采集正常车削、过渡阶段及发生颤振的振动信号.

分别用EMD和EEMD对3种工况的振动信号进行处理，其中EEMD加入系数k=0.25的随机高斯白噪声，执行100次.对EMD和EEMD的各阶IMF分量进行幅值谱分析，前3阶幅频图如图3和图4所示.根据奇异谱熵理论，对模式矩阵求奇异谱熵值.奇异谱熵值如表1所示.

图3 EMD的IMF幅频图

正常车削时，振动信号的能量在系统的固有频率处分布很集中，振动模式单一，熵值较小;发生颤振时，颤振主峰会明显加强，同时颤振频率倍频处峰值变大，因此频率分布相较于平稳阶段更分散，故熵值较大;过渡阶段，则介于两者之间.

由图3和图4可看出，正常车削时，频率特征主要集中在高频670 Hz左右处;过渡阶段，特征频率由原来的高频向低频移动;而颤振失稳阶段，在230，240 Hz附近都出现了明显的峰值，两频率的幅值相差不大，其倍频处的峰值也比较明显，频率成分更丰富.

从表1可看出，基于EMD和EEMD的奇异谱熵值方法均为颤振阶段的熵值最大，过渡阶段次之，正常车削时最小，与上述分析完全符合.但是前者3种工况下的熵值均大于后者.这是因为EMD方法存在模式混叠问题，使得信号的频率成分更复杂，而EEMD能较好地分离各个频率成分的信号，故其奇异谱熵值略小.因此，基于EEMD的奇异谱熵方法能更准确地判断出车削过程的工况.

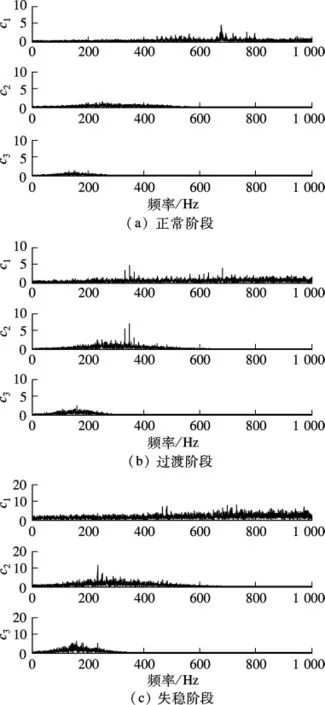
图4 EEMD的IMF幅频图

表1 振动信号的奇异谱熵

4 结语

EEMD通过添加不同的随机高斯白噪声，改变每次分析的频率特征尺度，多角度、多层次地剖析原始信号，有效抑制了EMD的模式混叠现象.

在实例分析中，利用EMD和EEMD对车削加工的振动信号进行分解，使得各频率特征分布在不同的时间尺度上.车削过程中各状态的频率特征不同，因而模式矩阵的奇异谱熵值不同，可通过奇异值熵的大小判断是否发生颤振.分别用基于EMD和EEMD的奇异谱熵法对实验数据分析对比，结果表明基于EEMD的奇异谱熵法能更有效地判断系统的工况，为旋转机械的故障诊断提供了有效的方法.

References)

［1］程军圣.基于Hilbert-Huang变换的旋转机械故障诊断方法研究［D］.长沙:湖南大学机械与装载工程学院，2005.

［2］ Lei Yaguo，He Zhengjia，Zi Yanyang.Application of the EEMD method to rotor fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2009，23(4):1327-1338.

［3］贾民平，凌娟，许飞云，等.基于基于时序分析的经验模式分解法及其应用［J］.机械工程学报，2004，40(9):54-57.Jia Minping，Ling Juan，Xu Feiyun，et al.Empirical mode decomposition based on time series analysis and its application［J］.Chinese Journal of Mechanical Engineering，2004，40(9):54-57.(in Chinese)

［4］ Ai Shufeng，Li Hui.Gear fault detection based on ensembleempiricalmodedecomposition and Hilbert-Huang transform［C］//Fifth International Conference on Fuzzy Systems and Knowledge Discovery.Jinan，China，2008:173-177.

［5］ Zhang Jian，Yan Ruqiang，Gao Robert X.Ensemble empirical mode decomposition for machine health diagnosis［J］.Key Engineering Materials，2009，413-414:167-174.

［6］张玲玲，骆诗定，肖云魁，等.集合经验模式分解在柴油机机械故障诊断中的应用［J］.科学技术与工程，2010，10(27):6745-6749.Zhang Lingling，Luo Shiding，Xiao Yunkui，et al.Application of EEMD in fault diagnosis of diesel engine［J］.Science Technology and Engineering，2010，10(27):6745-6749.(in Chinese)

［7］ Huang N E，Wu Z H.Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.World Scientific，2009，1(1):1-41.

［8］于德介，陈淼峰，程军圣，等.基于EMD的奇异值熵在转子系统故障诊断中的应用［J］.振动与冲击，2006，25(2):24-26.Yu Dejie，Chen Miaofeng，Cheng Junsheng，et al.Fault diagnosis approach for rotor system based on EMD method and singular value entropy［J］.Journal of Vibration and Shock，2006，25(2):24-26.(in Chinese)

［9］Wu Z H，Huang N E.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proceedings of the Royal Society，2004，460(2046):1597-1611.

［10］陈非，黄树红，张燕平，等.基于信息熵距的旋转机械振动故障诊断方法［J］.振动、测试与诊断，2008，28(1):9-13.Chen Fei，Huang Shuhong，Zhang Yanping，et al.Research on diagnosis of vibration faults rotating machinery based on distance of information entropy［J］.Journal of Vibration，Measurement and Diagnosis，2008，28(1):9-13.(in Chinese)