基于网络DEA的航空运输公司绩效分析

谭玉顺 陈森发

(1东南大学经济管理学院，南京 210096)

(2南京财经大学应用数学学院，南京 210046)

在航空运输高速发展的今天，我国民航运输总周转量增长迅速，但与欧美国家相比，我国民航运输业整体竞争能力依然较弱，在这种背景下，研究航空运输业的效率具有现实意义，数据包络分析(DEA)方法是广泛应用的分析工具.文献［1］利用随机前沿和DEA方法，检验了1976—1986年度欧美航空运输效率的差异.文献［2］运用DEA模型对国内5家航空公司2006年的运营效率进行了评价［2］.在这些研究中，都利用初始投入和最终产出评价航空公司运输有效性，没有考虑各航空公司的中间运营环节，因此无法确定运输中间过程的效率对整个运营过程的影响.航空运营过程可以分为2个子过程:①生产过程，即航空公司一定时期内的投入(人力、飞机数量、燃料用量等)和完成的飞行数量(航班数、飞行里程等);② 服务过程，即航空公司在已经完成飞行数量条件下，为人们出行、货物转移提供的服务数量.本文选取中国16家航空公司作为研究单元，建立了一种链式网络DEA模型，并利用该模型对航空公司的运输效率进行了全面评价.

1 网络DEA模型

数据包络分析法(DEA)是处理投入和产出之间转化效率的有效工具，在转化过程中把决策单元作为“黑箱”来处理.网络DEA模型把决策单元分为若干个子过程，每一个子过程都有相应的输入变量和输出变量，同时还有中间变量.通过这些中间变量，决策单元的各子过程建立了一定的联系.文献［3］在文献［4］的基础上给出了基于流程的单向网络DEA模型的一般形式;文献［5］给出了具有2个阶段的网络结构和效测量方法;文献［6-7］将网络DEA模型与多活动DEA模型进行了融合，建立了多活动网络DEA模型，将其应用于同步评价铁路客运和货运的技术效率和服务效率;文献［8］引入了Herbert和Lewis的网络DEA模型，分析了企业供应链绩效的评价过程;文献［9］构建了资源约束型2个阶段生产系统DEA模型，对我国商业银行的运作效率进行了评价;文献［10］研究了具有多阶段的链式网络DEA模型，给出了网络决策单元的网络有效性与阶段网络有效性的关系.

本文在文献［3-4］所给出的网络DEA模型的基础上，采用以方向性距离函数表示的链式网络DEA模型.考虑多个阶段网络结构的决策单元的相对有效性评价［4，10］(见图 1)，评价单元具有 k 个阶段，阶段S1利用初始投入z1得到阶段S1的产出z2，从阶段 S2开始，阶段 St的投入 zt是阶段 St－1(2≤t≤k)的全部产出，直到阶段 Sk得到最终产出zk+1.

图1 多阶段网络结构

1.1 方向性距离函数

设企业生产过程是将投入量x，转化为产出量y的生产技术过程，投入集L(y)、产出集P(x)、生产可能集T分别表示如下［11］:

生产模型必须满足生产过程中的基本属性，产出集为封闭、有界的凸集.生产可能集一般满足4条公理:凸性、锥形、无效性和最小性.企业经济活动中对生产技术的使用情况可用方向性距离函数表示，其定义为

式中，{－gx，gy}为给定的方向向量;β为方向性距离函数值［12］.其经济解释(见图2)为:生产可能集的一点C，沿方向{－gx，gy}逼近生产前沿面时与其交点为B，方向性距离函数表示在给定方向下，被观测点对生产前沿面偏离的测度，偏离越小，离生产前沿面越近，该点的生产率越高.

图2 方向性距离函数

文献［13］提出的投入与产出距离函数是方向性距离函数的特例，产出、投入距离函数分别为

产出距离函数表示某一产出向生产前沿面的最大限度的扩张或逼近，即某一产出和最大可能产出的比值;投入距离函数表示的某一生产点向理想的最小投入点最大限度的压缩比例.

如果选用基于投入的DEA模型，取gx=x，gy=0，则方向性距离函数与标准距离函数的关系为

如果选用基于产出的DEA模型，取gx=0，gy=y，则方向性距离函数与标准距离函数的关系为

为保证投入集和产出集的有效性，可知D(x，y;gx，gy)≥0.

1.2 技术效率

用方向距离函数来定义技术效率E，方向性距离函数的技术效率度量定义为0与1之间的一个指数，即

根据这个定义，当决策单元位于前沿面上时，方向性距离函数的值为0，相应的技术效率为1，根据该技术效率的大小可对决策单元进行排序.

2 航空运输系统网络DEA模型

2.1 建模思路

将航空运输过程分为2个过程，子过程1为航空运输生产过程，子过程2为航空运输服务过程，且运输生产过程的产出为运输服务过程的投入，航空运输过程结构如图3所示.

图3 航空运输过程结构图

由于这2个过程的内在联系，使得整个航空运输系统的运输效率受到2个子过程效率的影响.因此，本文采用一种网络DEA模型评价我国航空公司运输效率的整体有效性和各子过程运输效率有效性，进而分析航空公司子过程运输效率对整个生产运输过程效率的影响.

2.2 模型假设

假设在航空运输生产中，决策单元(DMU)的个数为J，初始投入要素种类为I，中间产出种类为M，最终产出种类为 S，参考集={(xj，yj):j=1，2，…，J}.设 DMUj为第 j个决策单元;xij为 DMUj生产消耗的 i的数量，其中 i=1，2，…，I;~ymj为 DMUj生产的中间输出 m 的数量，其中 m=1，2，…，M;ysj为DMUj的最终产出或服务s的数量，其中s=1，2，…，S;λkdj为在第d个生产子过程中衡量DMUk时DMUj的权重系数，其中d=1，2.

由方向性距离函数的定义，子过程1和子过程2的距离函数分别定义为投入距离函数与产出距离函数，即

本文采用DEA方法计算距离函数，通过求解相应的数学规划来获得函数值.

2.3 模型结构

子过程1、子过程2的生产可能集分别如下:

2.3.1 子过程DEA模型

对子过程1与子过程2分别使用input-C2R DEA模型和output-C2R DEA模型并对决策单元DMUk的技术效率进行有效性度量，即子过程1追求的是在输出不变的情况下，如何减少输入，从而达到有效率的状态;而子过程2是在输入(中间产出)不变的情况下，如何增加产出使达到有效率的状态.假设这2个子过程都为规模收益不变，子过程1 DEA评价模型P1为

子过程2 DEA评价模型P2为

由方向性技术效率的定义，可得到决策单元DMUk子过程1与子过程2的技术效率分别为

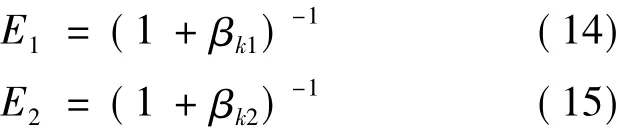
2.3.2 网络DEA模型

航空公司在整个运输生产过程的生产可能集可表示为

假设在规模收益不变的情况下，结合模型P1与P2建立评价网络决策单元DMUk效率的链式网络DEA评价模型P3如下:

对于该链式网络DEA效率，定义决策单元DMUk网络DEA模型的效率为2个子过程DMUk效率的几何平均数［9］，即

2.3.3 模型相关定义与性质

定义1设模型Pd(d=1，2)的最优解为，(d=1，2;j=1，2，…，J)，如果模型Pd(d=1，2)的最优集满足=0，则称决策单元DMUk在子过程d为弱DEA有效的.

定义2设模型P3的最优解为，如果模型的最优集满足==0，则称决策单元DMUk为网络DEA有效的.

定理1 决策单元DMUk为网络DEA有效的充要条件为决策单元DMUk在这2个子过程中均为弱DEA 有效，即==0.

充分性 决策单元DMUk在这2个阶段均为弱DEA 有效，即==0，若 DMUk不为网络 DEA有效，则由式(19)可知，决策单元至少有一个不为弱DEA有效，矛盾.

必要性 决策单元DMUk为网络DEA有效，即==0，下面证==0.反证，不妨假设＞ 0，由((1 －)x~) ∈T1及生产可能集的无效性知(~)∈T1，又由于¯θk2=0，有∈T2，从而＞0，=0为模型P3的可行解，但此时+=＞0，与DMUk为网络DEA有效矛盾，必要性得证.

3 网络DEA的有效性分析

本文采用客运量、客运周转量、货运量、货运周转量作为航空公司的产出指标;选择飞行班次、飞行里程和飞行小时数作为中间产出指标.由于数据的可获得性和局限性，选取各航空公司的飞机数量、燃料用量作为初始投入.数据均来源于2009年中国交通年鉴［14］.根据模型 P1～模型 P3和式(14)，(15)，(18)，利用 Lingo 编程，计算结果如表1所示.

根据计算结果，所有航空公司都无一为网络DEA有效，但航空公司整体运输效率平均值为0.889，效率值较高.在航空运输子过程1中，山东航空与金鹿航空运输效率最高，对应的有效度量值为1，为弱DEA有效;南方航空和东方航空效率较差，有效度量值都小于0.7.在航空运输子过程2中，中国航空、上海航空、春秋航空与奥凯航空效率最高，效率度量值均为1;山东航空、金鹿航空、东星航空效率较低.整个运输过程春秋航空、四川航空、奥凯航空、上海航空效率相对最高，排在这16家航空公司的前4位，而南方航空、东方航空、东星航空整体效率相对较低.

表1 各航空运输公司的效率评价结果

为了更好地体现各航空公司在2个子过程中的效率，参照2个子过程的效率平均值，构造效率分析矩阵(见图4).以航空公司2个过程的平均效率0.900，0.884为分界点，将其分为4个区域 A，B，C，D.显然在区域A的航空公司(春秋航空、四川航空和奥凯航空)2个过程效率都相对较高;区域C内的航空公司(东方航空、东星航空)2个过程效率都相对较低;区域B内航空公司(中国国航、南方航空、海南航空、上海航空)与区域D(山东航空等)7家航空公司在运输生产和服务效率上是不平衡的，其中中国国航等四大航空公司子过程2的效率高于子过程1，而山东航空等七大航空公司子过程2的效率低于子过程1.

图4 航空公司运输效率分析矩阵

4 结语

本文建立了以方向性距离函数表示的简单网络DEA模型，对我国16家航空运输公司在不同的运输生产过程中的技术效率进行了分析.该模型不仅能够对航空公司的整个运输过程效率的有效性进行度量，而且能够给出影响航空公司在各个运输子过程对无效率运输的影响程度，从而为航空公司管理部门提供调控的可行方向和尺度，因而比传统的DEA模型更具实际应用价值.

References)

［1］ Good D H，Röller L H，Sickles R C.Airline efficiency differences between Europe and the US:implications for the pace of EC integration and domestic regulation ［J］.European Journal of Operational Research，1995，80(3):508-518.

［2］蒋由辉，文军.基于DEA模型的中国主要航空公司的运营绩效评价［J］.科学技术与工程，2010，10(5):1175-1178.Jiang Youhui，Wen Jun.Operational performance evaluation of china main airlines based on DEA model［J］.Science Technology and Engineering，2010，10(5):1175-1178.(in Chinese)

［3］ Herbert F L，Thomas R S.Network DEA:efficiency analysis of organizations with complex internal structure［J］.Computers＆Operations Research，2004，31(9):1365-1410.

［4］ Färe R，Grosskopf S.Network DEA［J］.Socio-Economic Planning Sciences，2000，34(1):35-49.

［5］ Wade D C，Liang L，Zhu J.Measuring performance of two-stage network structures by DEA:a review and future perspective［J］.Omega，2010，38(6):423-430.

［6］Yu M M，Erwin T J L.Efficiency and effectiveness in railway performance using amulti-activity network DEA model［J］.Omega，2008，36(6):1005-1017.

［7］ Yu M M.Assessing the technical efficiency，service effectiveness，and technical effectiveness of the world’s railways through NDEA analysis［J］.Transportation Research Part A，2008，42(10):1283-1294.

［8］钟祖昌，陈功玉.基于网络DEA的供应链绩效评价方法与应用［J］.物流技术，2006(4):29-32.Zhong Zuchang，Chen Gongyu.Approaches and application of SC performance evaluation based on network DEA［J］.Logistics Technology，2006(4):29-32.(in Chinese)

［9］毕功兵，梁樑，杨锋.资源约束型两阶段生产系统的DEA 效率评价模型［J］.中国管理科学，2009，17(2):71-75.Bi Gongbing，Liang Liang，Yang Feng.A DEA-based efficiency-measuringmodel for two-stage production systems with constrained resources［J］.Chinese Journal of Management Science，2009，17(2):71-75.(in Chinese)

［10］魏权龄，庞立永.链式网络DEA模型［J］.数学的实践与认识，2010，40(1):213-222.Wei Quanling，Pang Liyong.Chain network DEA model［J］.Mathematics in Practice and Theory，2010，40(1):213-222.(in Chinese)

［11］ Jeon B M，Sickles R C.The role of environmental factors in growth accounting ［J］.Journal of Applied Econometrics，2004，19(5):567-591.

［12］Chambers R G，Chung Y，Färe R.Profit，directional distance functions，and Nerlovian efficiency ［J］.Journal of Optimization Theoryand Applications，1998，2(8):351-364.

［13］Shephard R W.Theory of cost and production functions［M］.Princeton，NJ，USA:Princeton University Press，1970.

［14］中国交通年鉴编辑部.中国交通年鉴2009［M］.北京:中国交通年鉴社，2009.