应用ARIMA模型预测福建省戊型肝炎疫情

2011-08-21谢忠杭欧剑鸣张莹珍黄文龙王灵岚

中国人兽共患病学报 2011年11期

谢忠杭，欧剑鸣，张莹珍，黄文龙，王灵岚

戊型肝炎（戊肝）是由戊型肝炎病毒引起的一种人兽共患病，临床症状类似于甲型肝炎，但病死率相对较高，主要经粪－口途径传播，可经水、食物等途径传播引起散发或暴发流行［1－2］；目前该病尚缺乏特效的治疗方法，也没有特异性免疫制剂可供预防［1－2］，因此监测资料的分析与预警是及时控制并减少其危害的关键之一；自2004年启动《疾病监测信息报告管理系统》至今，在全国范围内针对戊肝疫情做到了连续、系统、统一、高效、快速的收集，为其预测预警奠定了基础；故本文通过对福建省2004－2010年戊肝分月发病数的分析，根据其序列特点采用适当的ARIMA（autoregressive integrated moving－average，求和自回归移动平均）模型拟合其流行趋势，并对其进行为期1年的预测，为及时发现异常疫情提供科学依据。

1 材料与方法

1.1 资料来源《疾病监测信息报告管理系统》收集的福建省2004－2010年以发病日期统计的戊肝分月发病数（仅分析临床诊断和实验室诊断病例的已终审卡，但不包括删除卡）。

1.2 研究方法利用SAS 9.0软件的 PROC ARIMA综合软件包进行ARIMA模型的建模与分析［3］。

2 结果

2.1 序列的预处理

2.1.1 判断序列的平稳性：福建省2004－2010年戊肝分月发病数见表1，其时序图（图1）显示序列含有以年为周期的季节效应，虽表现出一定程度的上升趋势但总体趋势平稳；其自相关图（图2）呈现出明显的正弦波动规律，具有周期变化规律的非平稳序列的典型特征。

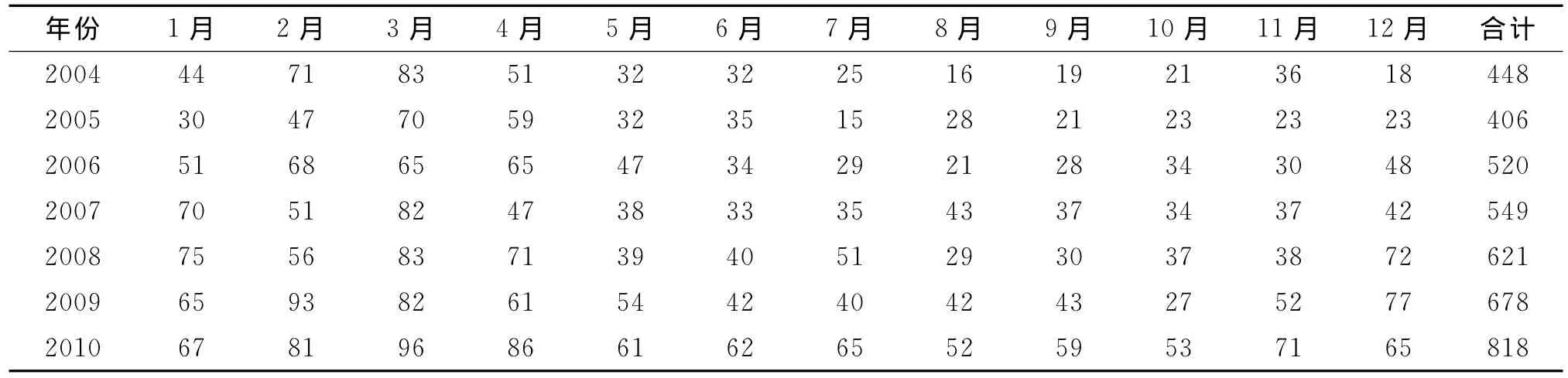
表1 福建省2004－2010年戊肝分月发病情况（例）Table 1 The monthly cases of hepatitis E from 2004 to 2010 in Fujian province

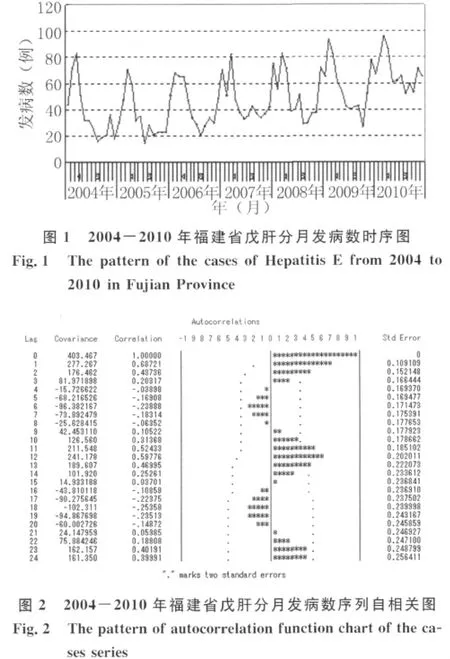
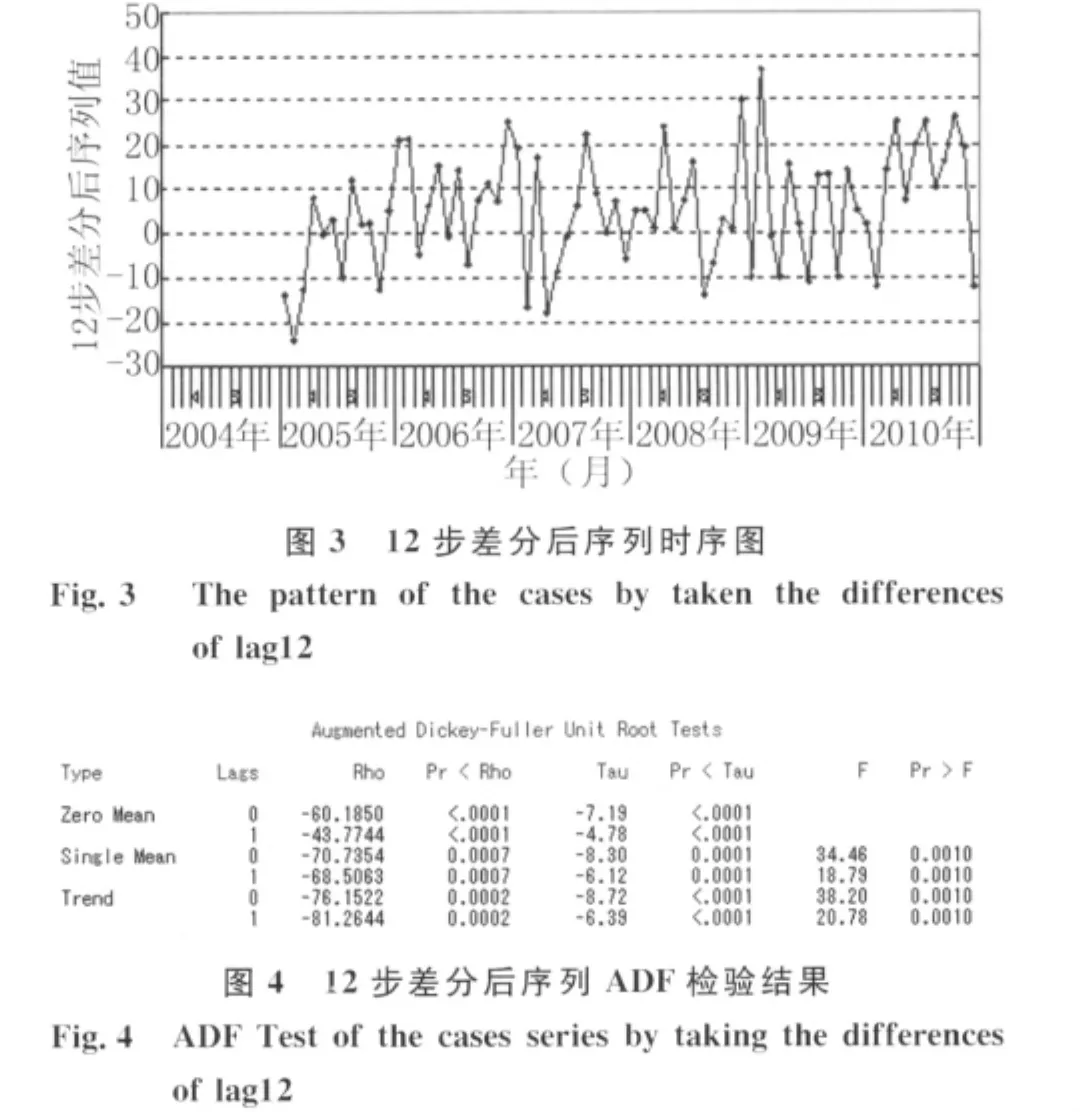
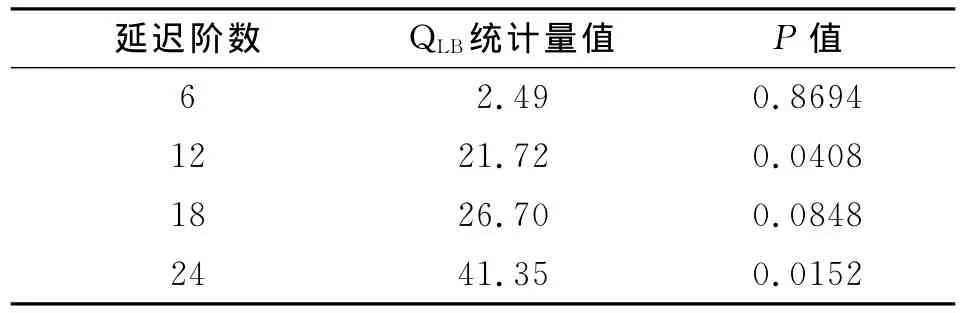
表2 12步差分后序列的白噪声检验Table 2 White Noise Test of the cases series by taken the differences of lag12

2.1.2 对原序列进行差分运算为提取原序列的季节效应，对原序列作12步差分，差分后序列的时序图（图3）和ADF检验结果（图4）示差分后序列平稳。

2.1.3 判断差分后序列的纯随机性通过对差分后序列进行白噪声检验，考察其纯随机性，检验结果（表2）显示，该差分后序列为非白噪声序列。

2.2 对差分后序列拟合ARMA模型差分后序列的自相关图（图5）和偏自相关图（图6）均显示：延迟12步自相关系数和偏自相关系数显著大于2倍标准差范围，其他几乎95%的都落在2位标准差的范围以内，说明差分后序列仍蕴含着显著的季节效应，即差分后序列仍存在季节相关性。故充分考虑各种可能，采用条件最小二乘法进行参数估计，并经模型和参数的显著性检验，拟合了2个显著有效模型（表3），经采用AIC准则和BIC准则评判其相对优劣，结果显示以 MA（（12））模型为相对最优模型［3］，用于预测最为合适，综合考虑前面的差分运算，该模型实际为乘积季节模型 ARIMA（0，0，0）×（0，1，1）12，其数学表达式为：

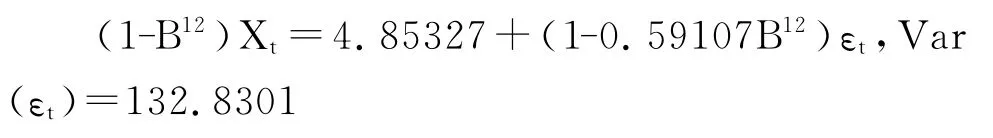
式中Xt为福建省戊肝分月发病数，B为延迟算子，εt为随机干扰。

图6 12步差分后序列偏自相关图Fig.6 The pattern of the partial autocorrelation chart of the cases series by taking the differences of lag12

2.3 进行序列预测根据拟合的相对最优模型ARIMA（0，0，0）×（0，1，1）12对未来12月戊肝发病数进行预测，结果见表4。

通过将该序列实际值、拟合值及预测值、95%置信区间上限联合作图（见图7），可以直观地看出该模型对序列的拟合效果良好。

表3 显著有效的2个备选模型参数估计比较Table 3 Parameter estimation of four ARIMA models

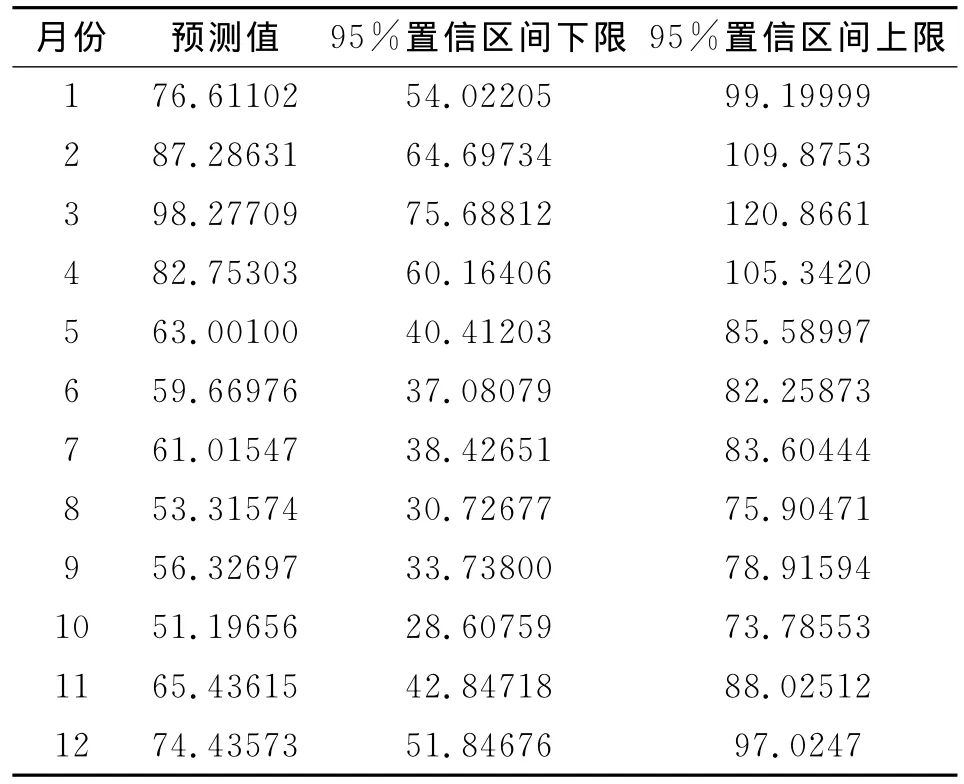
表4 预测2011年福建省戊肝分月发病数及其95%置信区间Table 4 Forecastings and limits of 95%UCL and LCL of Hepatitis E in Fujian province in 2011

图7 福建省戊肝分月发病数序列实际值、拟合值及预测值图Fig.7 The pattern of the actual cases and the fit cases of hepatitis ENote：Cases was showed on the Y axis with the date shown on X axis.The green lines with star marks showed the actual cases，the blue lines showed the fit curve（including forecasting values），the red lines with plus signs showed the line of 95%UCL，and the pink lines with circle signs showed the line of 95%LCL，respectively

3 讨论

从近年福建省戊肝分月发病数时序图（图1）中可以看出近年来福建省戊肝疫情平稳，无暴发或流行现象，控制效果良好。但因戊肝是一种急性人兽共患病，宿主多样且与人群接触密切［1－2］；传播途径多样，其中以粪－口途径传播为主，人群普遍易感，易引起食物或水源性流行爆发［1－2］；2003年起戊肝已成为本省福州地区急性病毒性肝炎的主要原因［4］；我省是乙肝高流行区［5］，可因混合感染导致病情加重［6］；普通人群戊肝病毒的感染率较高，提示亚临床感染的存在［7］，故其防控工作不可以掉以轻心，应密切关注其流行态势，并做好预测预警以严防暴发流行的出现。

ARIMA模型主要从序列自相关的角度揭示时间序列的发展规律［3］，既吸取了回归分析的优点又发挥了移动平均的长处，它根据数据序列的自相关系数、偏自相关系数建立起线性的数据间相互依赖的定量模型，既能解决数据自相关问题，又支持具有季节效果的数据建模，能较好地模拟历史疫情，并得到较好的预测效果，国内已有不少同行论证了该方法的适用性［8－13］。同时，结合本文资料特征，使用ARIMA模型相对优于其他预测模型：如需求序列值呈指数函数变化的灰色预测模型，对变量的分布有特殊要求、且要求变量独立、无法考虑变量间自相关性的回归模型或对数据要求较高的传播动力学模型等。

本文采用ARIMA模型建模，由图7可见拟合的相对最优模型 ARIMA（0，0，0）×（0，1，1）12对福建省近年戊肝发病数的拟合效果良好；该模型对未来12月内的预测值在疫情态势未发生显著变更时，能较好地预测疫情的未来走势及发病数；在疫情态势发生显著变更时（如暴发或流行时），则在疫情趋势变更至显著点（如超过95%的上限值）时，即可直观且客观地判定出疫情态势变更，并产出预警信息，为尽早介入并采取针对性防控措施提供有力的科学依据。

本文戊肝历史发病数的时间序列资料，其统计规则在地域上是以省为单位、在时间上是以自然月为单位、在例数统计上是以发病日期进行统计，故其预测预警受到这些统计规则的限制。但在实际应用中，可以根据需求适当调整这些规则，并建立其相应模型进行预测预警，如在地域上以地市或县区为单位，或时间上以周为单位，或在例数统计上包含疑似病例或以审核日期进行统计等。

但是，时间序列数据通常只适合做短期预测，如MA（q）序列理论上只能预测q步之内的序列走势［3］，故在实际应用中，应适时组织专家建立预警模型，如一年一度的疫情分析年会等；同时，应结合基于电脑的网络直报系统，增强其功能，方可在年度内实现预测值的自动修正预测功能以提高预测精度，并在疫情态势发生显著变更时及时、自动地发布预警信息。

综上所述，通过拟合戊肝发病数的相对最优ARIMA模型进行预测和预警，具有加强其防控工作的实际应用价值。

［1］仇家军，喻荣彬.戊型肝炎流行病学研究进展［J］.中华疾病控制杂志，2009，13（5）：572－576.

［2］吴婷，江浪.戊型病毒性肝炎研究进展［J］.中国疫苗和免疫，2009，15（4）：375－378.

［3］王燕，主编.应用时间序列分析［M］.2版.北京：中国人民大学出版社，2008：142－170.

［4］黄素钦，郑秀奇，吴秋芳.2000－2006年福州市传染病院急性病毒性肝炎流行病学分析［J］.海峡预防医学杂志，2007，13（6）：39－40.

［5］陈彩粼，黄文龙，洪荣涛，等.福建省2000—2008年乙型肝炎流行特征分析［J］.海峡预防医学杂志，2010，16（1）：46－48.

［6］张金良，高学武，辛克峰，等.散发性戊型肝炎的临床和流行病学特征分析［J］.实用肝脏病杂志，2008，11（3）：182－183.

［7］王惠榕，严延生，萧剑雄，等.福建省不同人群中戊型肝炎病毒感染的血清流行病学调查分析［J］.中国人兽共患病学报，2007，23（4）：370－372.

［8］黄春萍，邓晶，张磊，等.ARIMA模型在麻疹预警中的应用［J］.疾病监测，2008，23（1）：53－55.

［9］冯丹，韩晓娜，赵文娟，等.中国内地法定报告传染病预测和监测的 ARIMA模型［J］.疾病控制杂志，2007，11（2）：140－143.

［10］吴家兵，叶临湘，尤尔科.时间序列模型在传染病发病率预测中的应用［J］.中国卫生统计，2006，23（3）：276.

［11］钟球，蒋莉，周琳，等.广东省结核病发病趋势的时间序列分析［J］.中国防痨杂志，2010，32（9）：515－519.