复合材料加筋板的阶梯式挖补修理稳定性分析

徐建新，曹小梅，李顶河

（中国民航大学航空工程学院，天津 300300）

复合材料加筋板结构相对于层合板结构，能够承受较大的载荷，被广泛应用于飞机的蒙皮和壁板，如ARJ-21垂尾壁板、B777垂尾和平尾壁板，同时可降低飞机重量，提高飞机的飞行效率，如航空发动机GE90。因此对复合材料加筋板的损伤的修理研究是民机复合材料结构修理的关键问题。目前复合材料结构主要的修理方式为机械连接修理、胶接修理和机械-胶混合连接，其中机械连接在修理过程中要在原结构上开孔，在修理区域容易引起应力集中现象，破坏了复合材料纤维性能和结构的连续性。而这些修理方法还会降低飞机上复合材料的静、动态承载性能，严重时威胁航空器的安全。因此当前对于复合材料结构损伤的修理，大多采用胶接修理的方法[1]。

对于胶接修理，主要有三种修理方案：斜接以及阶梯形挖补修理、单面贴补修理、双面贴补修理。其中对于受冲击损伤的复合材料加筋层合板，挖补修理是一种非常有效的结构修理方式。对于曲率较大或有气动外形要求较高的表面，挖补修理具有一定的优越性，而且胶接表面的剪应力分布比较均匀，同时可以最大限度地恢复结构的刚度和强度，可见在复合材料层合板维修中得到了广泛的应用[2]。目前越来越多的学者关注复合材料的修理研究，并进行了一系列的试验工作，如Atas C和Akgun Y[3]对玻璃纤维/环氧树脂复合材料板冲击响应进行研究，样品取得了良好的修复效果。孟凡颢[4]等对复合材料挖补修理结构进行试验分析，结果表明挖补修理可使受损件的强度恢复90%以上，取得了良好的修复效果。同时在理论分析方面[5-6]，采用有限元方法进行初步探讨，如Sout和Hu[7]在斜接式搭接研究的基础上，通过有限元计算对挖补修理结构进行失效原理分析。王宇光[8]介绍了复合材料层合板挖补的研究现状，其中涉及了阶梯式挖补的修理现状。Hart Smith[9]介绍了复合材料阶梯式挖补的修理方式。陈光伟[10]等人研究了阶梯型对接层合板复合材料力学性能，测定了2D玻璃纤维机织物层合板复合材料的拉伸和弯曲强度。而且在胶接修理中，稳定性的研究又是复合材料修理的主要领域之一。针对板壳结构的稳定性分析国内外开展了很多研究，目前很多文献[11-16]用各种解析和数值的方法研究了不同边界的各向异性矩形板的稳定性问题。本文将针对复合材料加筋层合板的阶梯式挖补稳定性进行详细分析。

本文主要应用MSC.Patran有限元软件对复合材料加筋层合板在阶梯式挖补修理方式下的屈曲行为进行了数值模拟，详细研究了补片半径、修补阶梯数、筋距等参数对其修补稳定性的影响规律，由此得出了修补板的屈曲特性，得出的结论为复合材料结构修理方案的设计提供了一定的有价值的参考依据。

1 几何模型

加筋层合板阶梯挖补修理几何模型如图1所示，层板为对称结构，含中心孔损伤。其中板长、宽为a=b=400 mm，厚度t=2.4 mm。筋厚度ts=4 mm，高度ds=10 mm，筋边到板边距离L。损伤孔直径d=20 mm，补片最大直径D为变量。

图1 复合材料加筋层合板结构修补的几何模型Fig.1 Model of stiffened composite laminates with stepped-lap repair

复合材料层合板和补片材料均为Celion/LARC-160，采用相同的铺层结构，即[0°/-45°/45°/90°]s，共分为8层，每层厚度为0.3 mm。在有限元计算中，将其假设成均匀正交各向异性的线弹性材料，材料性能参数如表1所示。

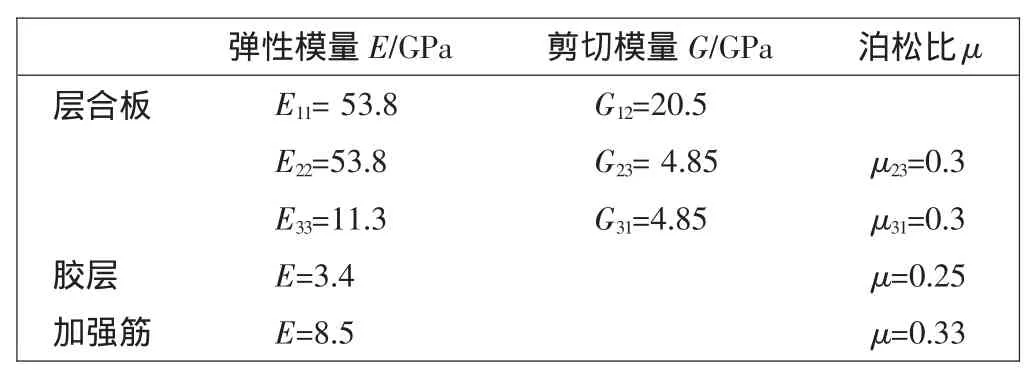
表1 材料性能参数Tab.1 Material of properties of plate,adhesive and stiffener

2 有限元建模

本文主要针对薄的航空复合材料层合板进行结构建模分析，为了准确地对复合材料加筋层合板阶梯式挖补的屈曲变化趋势进行描述，胶层和层板的主要部分采用六面体等参体元来构造，中心圆板用三棱柱等参元来模拟。由于是层合板模型，需按不同方向铺层，为了建模过程中定义材料属性的方便，将除胶层以外的其他每部分分为 4 组，即 0°组、-45°组、45°组、90°组。每一组都由建好的有限元网格的面单元拉伸不同距离得到，幷确定当所有组显示在一起时能够组成一块完整无间隔的板。补片和模板通过拉伸得到。胶层和加强筋不需要铺层，也由拉伸得到。在建模的最后，消除重复节点是必不可少的一步。

3 算例分析

3.1 补片最大半径和阶梯数

取筋边到板边距离L=100 mm，对建好的模型施加边界条件，该加筋板一端固支，一端施加压力，F=2.4×105N。选择生成结果的分析类型为屈曲分析SQL105，定义求解参数中特征值提取数为1。随后提交到MSC.Nastran进行计算，最后读入分析结果。

3.1.1 补片最大半径

取修补阶梯数为3和4，对同一种阶梯数不同半径的加筋层合板进行屈曲分析，取不同的补片最大半径r为22 mm、28 mm、34 mm、40mm，屈曲因子变化趋势如图2所示。

通过图2不同补片最大半径对应的第一阶屈曲因子变化曲线可以反映出，随着补片半径的增大，屈曲因子逐渐增大，说明半径越大，临界载荷越大，稳定性越好；而且还反映出阶梯数为3所对应的屈曲因子大于阶梯数为4的屈曲因子，所以阶梯数影响着不同补片半径下的屈曲因子；同时，当阶梯数为4时，随着补片半径的增大，临界载荷变化小，稳定性趋于平缓。所以当修补阶梯数一定时，随着补片最大半径的增大，板的修补稳定性逐渐增大。所以在实际修理操作中根据挖补的阶梯数，补片在一定的范围内越大越好，但这也要确保能在实施的基础之上进行修补。

3.1.2 修补阶梯数

取补片最大半径r为40 mm和48 mm的不同阶梯数的加筋层合板进行屈曲分析，取阶梯数为2、3、4、5，屈曲因子变化趋势如图3所示。

通过图3的不同补片阶梯数对应的第一阶屈曲因子变化曲线可以反映出，随着补片阶梯数的增大，当补片最大半径为40 mm时屈曲因子总体趋势是先增大后减小又增大的；当补片半径为48 mm时，随着阶梯数的增大，屈曲因子是先减小后增大的；当补片半径越大时，修补的屈曲因子越大，稳定性越好。所以，不同补片半径在阶梯数的变化下呈现出不同的变化趋势。因此在实际修补操作过程中需进行精确的计算之后再确定修补梯数。

3.2 筋距

取阶梯数4，取修补最大半径r为28 mm，取筋高ds为8 mm和10 mm，对筋边到板边距离的取值L为80 mm、90 mm、100 mm、110 mm、120 mm。对筋边到板边距离L变化的加筋层合板进行屈曲分析，屈曲因子变化趋势如图4所示。

通过图4的不同筋距对应的第一阶屈曲因子变化曲线可以反映出，随着两根筋之间筋距的增大，屈曲因子在增大，而且也反映出筋越高，屈曲因子越大，临界载荷越大，稳定性越好，但在实际的修补中要考虑筋的重量对设计的影响，因此在实际的修补中，筋距要经过精确的计算来确定。

4 结语

本文主要应用MSC.Patran有限元软件，建立了复合材料加筋层合板的有限元模型，并在一定的作用力下，对复合材料加筋层合板的屈曲行为进行了数值模拟，详细研究了补片最大半径、修补阶梯数和筋距对其修补效果的影响规律。由此得出以下结论：

1）对于相同的修补阶梯数，取不同的最大补片半径时，随着补片最大半径的增加，板的临界载荷逐渐增大，板的稳定性就增大了，而且阶梯数越小，所对应的临界载荷越大，稳定性越好；对于相同的补片最大半径，取不同修补阶梯数时，随着修补阶梯数的增加，临界载荷呈现出一定的规律性，而且当半径越大，对于相同的修补阶梯数，对应的临界载荷就越大，稳定性就更好。

2）对于相同的修补阶梯数和最大补片半径，当两根筋之间的距离在不断增大时，临界载荷也在不断增大，而且当筋的高度越高，所对应的临界载荷越大，稳定性越好。

[1]陈绍杰.复合材料结构修理指南[M].北京：航空工业出版社，2001.

[2]薛克兴.复合材料结构的损伤与修补[M].北京：航空工业出版社，1992.

[3]ATAS C，AKGUN Y.An experimental investigation on the low velocity impact response of composite plates repaired by VARIM and hand layup processes[J].Composite Structures，2011，93（3）：1178-1180.

[4]孟凡颢，陈绍杰，童小燕.层压板修理设计中的参数选择问题[J].复合材料学报 ，2001，18（4）：28-31，68.

[5]BARUT A，HANAUAKA J，MADENCI E.Analysis method for bonded patch repair of a skin with a cutout[J].Composite Structures，2002，55（3）：277-294.

[6]ENGELS H，BECKER W.Closed form analysis of external patch repairs of laminates[J].Composite Structures，2002，56（3）：259-268.

[7]SOUTIS C，HU F Z.Failure analysis of scarf patch repaired carbon fiber/epoxy laminates under compression[J].AIAA Journal，1998，38（4）：737-740.

[8]王宇光，黎关生.复合材料结构修理研究现状[J].航空维修与工程，2003（3）：31-34.

[9]HART-SMITH L J.Adhesive-Bbonded Scarf and Stepped-Lap Joints，NASA-CR-112237[R].Hampton，VA：Langley Research Center，1973.

[10]陈光伟，王富有，张国利，等.阶梯型对接层合板复合材料力学性能的试验研究[J].材料工程，2009（2）：182-185.

[11]DAWE D J，CRAIG T J.The vibration and stability of symmetrically laminated rectangular plate subjected to in-plane stresses[J].Composite structures，1986，11（5）：281-307.

[12]HU HR，BADIR AR，ABATAN A.Buckling behavior of a grahite/epoxy composite plate under parabolic variation of axial loads[J].International Journal of Mechanical Science，2003，45（6）：1135-1147.

[13]PURBOLAKSONO J，ALIABADI M H.Buckling analysis of shear deformable plates by boundary element method[J].International Journal for Numerical Methods in Engineering，2005，62（4）：537-563.

[14]KANG JH，LEISSA ARTHUR W.Exact solutions for the buckling of rectangular plates having linearly varying in-plane loading on two op posite simply supported edges[J].International Journal of Solids and Structures，2005，42（14）：4220-4238.

[15]PALARDY R F，PALAZOTTO A N.Buckling and vibration of composite plates using the levymethod[J].Composite Structures，1990，14（1）：61-68.

[16]SHERBOURNE A N，PANDEY M D.Differential guadrature method in the buckling analysis of beams and composite plates[J].Computers and Structures，1991，40（3）：903-913.