基于统计置信度的湍流检测门限确定方法

卢晓光，夏 冬

（中国民航大学智能信号与图像处理天津市重点实验室，天津 300300）

湍流是造成飞机颠簸的主要原因，严重影响着飞行的安全性[1]。机载气象雷达是一种重要的航空电子设备，具有气象探测、气象回避等功能，它为航空运输的安全性提供了保障，是民航飞机的“双眼”。机载气象雷达都具有湍流检测的功能[2]，可以探测飞机前方存在的湍流区域，从而引导飞行员避开这些危险区域，保障飞行的舒适性与安全性。

湍流是由大量不规则运动的微粒组成的，而且这些微粒的速度在较小的范围内变化剧烈，具有较宽的速度谱，即速度偏差较大。雷达的出现使湍流检测成为可能。最早通过雷达反射率因子即雷达回波幅度判断[3]，准确度不高；多普勒雷达出现后，利用速度谱宽的判断方法出现[4]，也是目前机载气象雷达最常用的方法。在近几年，研究者又提出了诸如旋涡分散率等一些新的检测量[5-6]，但计算起来较复杂，或者需要其他的辅助信息。最简单而且实际中普遍使用的是谱宽法，也是目前民航机载气象雷达应用的方法[7]。对民用客机而言，一般认为速度偏差大于5 m/s的气团即为湍流目标[7]。机载气象雷达正是通过测量气象目标的速度信息检测湍流，比较目标回波信号的谱宽与预设湍流门限的大小判别湍流的存在性[2，8-9]。机载气象雷达是脉冲多普勒雷达，通过对目标的多次采样探测气象信息。由于气象目标是体目标，其回波是由大量散射粒子叠加而成，回波会具有一定的起伏，对同一目标不同脉冲采样的回波不尽相同，判断的结果当然会有差别。测出的谱宽值有的大于门限，有的小于门限。那么，究竟如何可靠地判断该目标是否为湍流，即检测门限的确定。由于微粒随机运动，这个问题本质上是一个统计学问题，本文引入统计学中置信度[10]的概念来进行检测门限的判断，即将检测门限与检测的可靠性联系起来，通过统计学中置信度来确定检测门限。

1 机载气象雷达湍流检测流程

气象目标是由大量散射粒子组成的，是分布式目标。当雷达波照射时，大量粒子（各自具有随机相位）散射电场的叠加可得到一个高斯统计信号。由于粒子相互运动，因此还存在一个多普勒扩展，通常被称为多普勒谱方差。所以，气象目标的回波功率谱呈现高斯谱的特性[11]，且谱宽与气象目标的类型有关。湍流内部的粒子运动较为剧烈，因而具有较大的谱宽，一般认为速度谱宽大于5 m/s，如图1所示。

为了有效检测湍流的存在，现代民航飞机无一例外地安装了具有湍流检测功能的机载气象雷达。它是利用多普勒效应来探测湍流目标，雷达接收到目标回波后，提取目标回波的相位信息，通过一定的信号处理手段，经过统计分析得到目标的速度谱宽，再与湍流阈值相比即可判断目标是否为湍流。具体的实现步骤随不同的处理方法而不同，这里介绍一下检测湍流的常用方法——脉冲对探测法的处理流程。脉冲工作方式的“脉冲比较法”检测原理电路如图2所示。处理I、Q信号可以得到信号的相位信息，其与速度有关。第一次比较电路计算相邻重复周期的回波信号的相位差，获取当前时刻目标的多普勒速度。经过积累平均，可以获取目标的平均速度。经过第二次比较，即计算第一次比较后得到的相位与平均相位之差的绝对值，即相位偏差，与速度偏差相对应。门限检测就是以速度偏差为5 m/s对应的相位为门限，判断偏差相位是否超过该门限。由于气象目标包含大量的微粒，其雷达回波是这些微粒回波信号的叠加，因而具有随机信号的特点，仅仅通过一次判断是不能进行检测的，需要经过统计来分析是否为湍流目标。原理图中统计分析即是实现这一功能的，如统计分析后认为大于68%的回波位于湍流谱宽门限内，则该目标为普通的降雨目标；否则，即少于68%的回波位于湍流谱宽门限内，该目标被判断为湍流。由于是统计分析，这里的门限与置信度（描述判决结果的可信程度）相关，因此可称为置信度门限，即设置的门限可使统计结果的置信度达到所要求的门限，则关键是置信度门限的确定。

2 湍流检测置信度门限的确定

前面提到，在湍流检测的统计分析步骤中，需将统计得到的速度偏差超过湍流门限的个数与置信度门限做比较，超过门限即判断为湍流，否则为普通降水目标。那么，这个门限是怎么确定的，下面从统计学的角度来分析这个问题。

湍流的速度分布呈现高斯谱的特性，且速度谱宽至少为5 m/s。如图3所示，画出了几种不同的速度分布特性，其中“+”标记的为普通降水，另两个为湍流。两条竖线表示的是湍流的门限。

以σ=5（临界湍流）为例，计算速度绝对值小于5 m/s的概率，为

则对于湍流来说，肯定存在p≤68%。因此在湍流检测中，可以统计速度在（-5，5）之间的概率，然后与68%进行比较，从而做出是否为湍流的判断。但是，在实际当中，由于样本有限，不可能得到p的真实值，只能通过速度样本来估计。另外，在湍流检测时，为了做出判断我们所关心的是p是否小于68%，而并不需要知道其真实值，因此需要做的就是判断估计到的p＾是否以很大的可能性落于68%的范围之内，也就是说只需要得到p的一个粗略估计。

用数学模型表示，这实质上是一个参数估计的问题。假设检测时积累的脉冲数为n，其中速度偏差小于5 m/s的样本个数为k，统计分析就是对速度偏差小于5 m/s的概率进行估计。由概率统计中的贝叶斯公式得，

其中：p为速度偏差小于5 m/s的概率；f（p）为p的概率密度函数；l表示n个速度偏差样本中速度偏差小于5 m/s的个数为k这一事件，且由二项式分布可知P{l|p}=pk（1-p）n-k。则式可变为

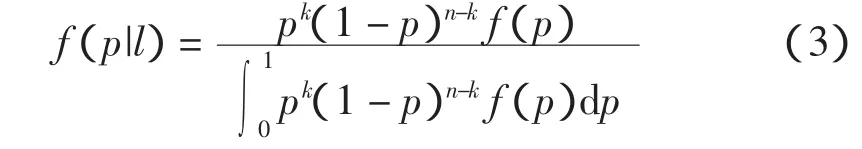
对于p我们没有任何先验信息，此时可假设p为一个在[0，1]均匀分布的随机变量，令f（p）=1代入式（3），得

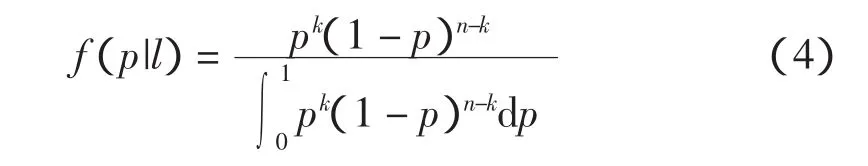
又 则

可见当l发生时，p服从的是β-分布[12-13]。

下面引入一个统计置信度，其定义为经过一系列试验，某事件A的实际概率小于规定水平的几率（定义中的实际概率是指有限次试验多的概率在试验趋向无限时的极限值）。应用于估计事件A发生的概率p，统计置信度可阐述为进行n次试验，事件A发生k次的条件下事件A发生的概率不大于规定水平的概率，即

其中：CL为置信度；P[]为概率。根据上面的定义可知，CL是一种概率，其可能的取值范围为[0，1]。从物理意义上讲，CL表示接受某一事件的可信度。

在湍流检测中，由式（4）和式（5）得

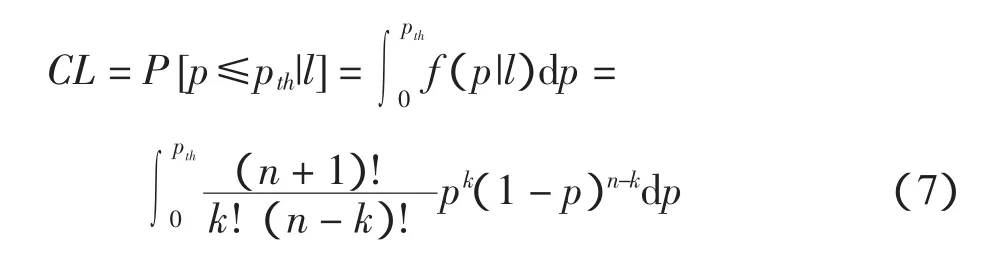
其中pth=68%。

这里以n=10为例，计算n个速度偏差样本中速度偏差超过门限5 m/s的个数k取不同值时，速度偏差小于5 m/s的概率小于68%这一事件的可信度。为了比较，还做了pth为50%、60%和75%时的置信度，结果如图4所示。

从图4可看到，当且仅当速度偏差超过门限5m/s的个数大于等于6时，认为速度偏差小于5 m/s发生概率小于68%的可靠性为95%，因此当n=10时，可得到湍流检测的95%置信度门限：速度偏差大于等于5 m/s的个数为6，即当且仅当速度偏差大于等于5 m/s的个数至少为6时，才可认为气象目标为湍流。

3 实验仿真结果与分析

为了验证方法的有效性，利用仿真的气象雷达回波信号进行了实验。实验设置如下的场景，在飞机前方存在5个气象目标区域，包括湍流目标和普通气象目标，其中2个降雨区域，3个湍流区域，假设微粒的速度服从高斯分布，可以通过谱宽的大小来区分是否是湍流目标。具体场景参数如表1所示，飞机位于坐标原点处，向前方飞行，雷达从左向右扫描，探测前方的气象目标。根据气象雷达的工作过程利用文献[14]的方法进行了雷达回波的仿真，仿真时实验条件模拟Collins公司的机载气象雷达WXR-2100湍流模式[7]。图5为微粒的径向速度分布图，可见存在湍流区域的微粒速度间变化剧烈。

表1 仿真气象场景的参数Tab.1 Simulated meteorological scenes

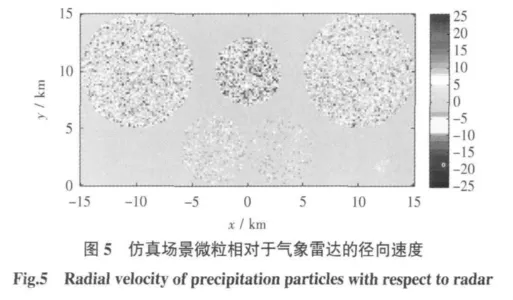
接下来根据湍流的检测流程，对仿真的机载气象雷达信号进行处理。在湍流检测时第一次平均脉冲积累数和统计分析所用脉冲积累数均为10，根据前面的理论分析可知湍流门限为5 m/s和检测门限为速度偏差大于5 m/s的个数为6。如图6所示，为检测结果。从图6可以看到，通过湍流检测，位于上方的3个气象区域中的大部分被判别为湍流，而其他两个区域没有检测出湍流，这与实际假设相吻合，可见根据理论得到的检测门限是合理的。另外从图6还可以看出，3个湍流区域检测出存在湍流的距离单元数目不同，中间的大部分单元存在湍流，左边的区域次之，右边的区域数目最少，这是由于湍流的强度不同造成的，其结果与表1设置的相符合。

4 结语

检测门限的设定对湍流的自动检测至关重要，过小会引起虚警，过大又会造成湍流的漏报而带来灾难性的后果。本文引入统计学中的置信度概念，利用统计学的理论推导了机载气象雷达湍流检测时检测门限的确定方法。对仿真气象雷达信号的实验证明了所得到的检测门限正确，能够检测出湍流区域，从而对湍流做出预警。

[1]KAPLAN M L，HUFFMAN A W，LUX K M.Characterizing the severe turbulence environments associated with commercial aviation accidents[J].Meteorology and Atmospheric Physics，2005，88（3－4）：129－152.

[2] 蔡成仁.彩色气象雷达[M].北京：北京国防工业出版社，1992：13－30.

[3] LEE J T，MCPHERSON A.Comparison of Thunderstorms over Oklahoma and Malaysia Based on Aircraft Measurements[C]//In Proceedings of the International Conference on Atmospheric Turbulence，London，1971：1－13.

[4] DOVIAK R J，ZRNIC D S.Doppler Radar and Weather Observations[M].New York：Academic Press，1993.

[5]CORNMAN L，MEYMARIS G，MARTHA LIMBER.An Update on the FAA Aviation Weather Research Program′s in Situ Turbulence Measurement and Reporting System[C]//11thConference on Aviation，Range and Aerospace Meteorology，Hyannis，MA，American Meteorological Society，2004.

[6]PROCTOR F H，HAMILTON D W.Turbulence Hazard Metric Unification[R].Oral Presentation，NASA Weather Accident Project Review，Williamsburg，VA，2005.

[7] ROCKWELL COLLINS.WXR －2100 MultiScan Radar Operator′s Guide[G].2007.

[8]苏卉芳.民航机多普勒气象雷达的湍流检测[J].电子技术，1989（4）：153－158.

[9] 陈惠萍.多卜勒湍流检测[J].中国民航学院学报，1990，8（4）：38－46.

[10]吴从中.数字通信系统中误码率的估计方法[J].合肥工业大学学报（自然科学版），2002，25（1）：113－116.

[11]ZRNIC D S.Estimation of spectral moments for weather echos[J].IEEE Transaction on Geosciences Electronics，1979，GE－17：113－128.

[12]AGRESTI A，COULL B A.Approximate is better than“exact”for interval estimation of binomial proportions[J].American Statistics，1998，52：119－126.

[13]VOLLSET S E.Condence intervals for a binomial proportion[J].Statistics in Medicine，1993，12：809－827.

[14]CHEONG B，PALMER R，M XUE.A time－series weather radar simulator based on high－resolution atmospheric models[J].Journal of Atmospheric and Oceanic Technology，2008，25（2），230－243.