桥梁结构基于校验系数损伤程度的研究
2011-07-31张献民
张献民,李 惠
(中国民航大学机场学院,天津 300300)
近些年来无论国内还是国外,桥梁倒塌的事故频频发生[1],众多由于桥梁损伤而导致桥梁倒塌的例子向我们发出严重警告,许多现有的桥梁已不能满足现代交通运输量的使用要求,桥本身已经出现不同程度的损伤与承载力下降问题,需要及时进行检测监测并对其进行维修加固处理。
无论是公路铁路桥梁还是机场滑行道桥,桥梁试验对桥梁结构的损伤检测都具有十分重要的意义。桥梁试验一般分为静荷载试验和动荷载试验。静载试验是将静载作用在桥梁上的指定位置而测试结构的静应变、静位移以及其他试验项目,从而推断桥梁结构在荷载作用下的工作状态和使用能力。在静载试验中校验系数是一个重要的评测指标[2],而目前许多文献对校验系数的研究仅仅在于对比它的值是否符合规范标准,而没有把校验系数和损伤程度联系起来。本文针对这种情况,结合有限元软件ANSYS模拟T型梁在不同荷载作用下挠度的变化来探索损伤程度和校验系数的关系,为桥梁的无损检测提供了新思路。
1 理论基础
1.1 结构跨中位置的挠度

1.2 梁构件承载力评定方法—校验系数η法
校验系数η是评定结构工作状态、评定桥梁承载力的一个重要指标,可以从中判定桥梁结构的承载能力的工作状态。校验系数η是试验实测值与理论计算值的挠度之比,它反映结构的实际工作状态。即

一般来说η≤1说明理论计算偏安全,结构尚有一定的安全储备,在这个情况下说明桥梁结构的工作状态良好,η值越小表明结构的安全储备越大。由于本文研究的是有一定损伤程度的桥梁的校验系数,因此校验系数均η≥1。
1.3 基于频率变化对桥梁的检验
采用极限频率作为结构模态参数进行桥梁结构检验,由振动力学可知,结构的固有频率的表达式可写成如下形式

由上式可以看出,结构的固有频率是质量m、截面尺寸、材料的函数。当桥梁整体承载力下降时结构的抗弯刚度EI也会相应减小,而质量变化不大从而结构的固有频率相应减小。
综上所述,抗弯刚度EI的变化和挠度、校验系数以及频率都有着密切关系,所以本次课题着重研究当抗弯刚度EI发生一定变化即桥梁有一定损伤情况下,校验系数的变化规律。
2 理论分析
2.1 ANSYS模型的建立
1)本文根据河北省某桥为原型建立T型梁,T型梁的翼缘的宽度B为1 480 mm,翼缘的高度hf为80 mm,T型梁的高h为1 160 mm,跨度分别取L1=15 m,L2=17.5 m,L3=19.96 m。
2)本构关系的选取:混凝土的本构关系采用E.Hongnestad表达式表示混凝土的单轴应力应变关系式。在ANSYS建模时,认为应力应变关系式拉压相等,由于混凝土材料受拉段非常短,认为拉压相同影响小。纵向钢筋的应力应变关系采用理想弹塑性模型,如图1和图2所示

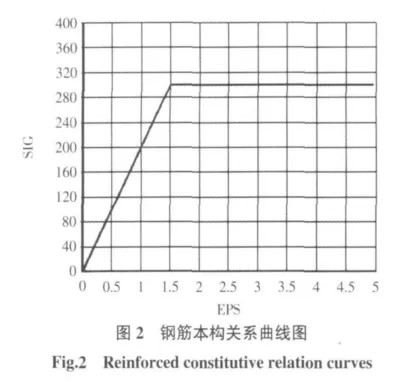
3)ANSYS仿真建模中,混凝土采用SOLID65单元,计算模型假定混凝土与钢筋粘结良好,不考虑二者之间的滑移,采用的是分离式模型,混凝土强度等级C30,钢筋采用二级钢筋,纵筋采用LINK 8。划分单元时,为保证计算精度,单元尺寸尽可能小些,钢筋混凝土采用分离式建模的方式,并进行了耦合。具体参数以及模型如表1和图3和图4所示[4-6]。

表1 混凝土,钢筋材料模型参数数据表Tab.1 Concrete and steel material model parameter data table

2.2 检验系数与损伤程度计算关系的建立
2.2.1 损伤程度与频率的关系
15 m、17.5 m、19.96 m跨长的T型完好梁以及各个损伤程度下一阶频率的变化,如表2所示。

表2 不同跨度不同损伤程度下频率的变化值Tab.2 Frequency changes value under different span and degree of damage
根据文献[7]的研究表明,当桥梁的频率降至完好桥梁的75%~85%时,认为桥梁已不能使用,本文取15%作为标准,因此由表1可以看出,损伤程度在30%时,频率下降了16.27%,因此损伤程度取到30%为止,关系图如图5所示。

2.2.2 损伤程度与校验系数的关系研究
基于本课题主要研究挠度值的变化和损伤程度的关系,为了使研究更具一般性分别模拟了三种跨径,不同损伤程度的T型梁在跨中位置施加不同等级的荷载作用,梁的挠度值的变化,具体数据如表3、4、5所示。
根据表3、表4、表5分别拟合出不同等级荷载下校验系数和损伤程度的关系曲线并拟合成公式,如图6,7,8 以及表 6、7、8 所示。

表3 跨径15 m T型梁损伤程度和校验系数数据表Tab.3 Data table of 15m T beam about damage degree and calibration coefficient

表4 跨径17.5 m T梁损伤程度和校验系数Tab.4 Data table of 17.5 m T beam about damage degree and calibration coefficient

表5 跨径19.96 m T梁损伤程度和校验系数Tab.5 Data table of 19.96 m T beam about damage degree and calibration coefficient


表6 15 m T梁不同荷载等级下损伤程度和校验系数的关系式Tab.6 The equation of 15 m T beam about damage degree and the calibration coefficient

表7 17.5 m T梁不同荷载等级下损伤程度和校验系数的关系式Tab.7 The equation of 17.5 m T beam about damage degree and the calibration coefficient

表8 19.96 m T梁不同荷载等级下损伤程度和校验系数的关系式Tab.8 The equation of 19.96 m T beam about damage degree and the calibration coefficient
由表6、表7、表8可以看出损伤程度和校验系数的关系可以表示成
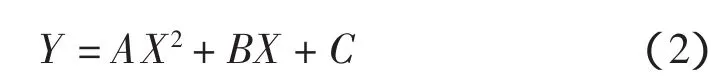
其中:Y为损伤程度%;X为校验系数。
3 结语
1)结构的损伤程度和频率的下降幅度呈一一对应的关系。
2)由校验系数和损伤程度的关系曲线可以看出,当作用的荷载等级较低时,结构处于弹性阶段,此时校验系数的值一定。随着荷载等级的加大以及损伤程度的加深,结构进入了弹塑性阶段,这时候校验系数是随着荷载等级、损伤程度发生相应的变化。
3)建立了校验系数与损伤程度、梁的跨度之间的数学模型关系式,为桥梁的无损检测提供了新思路。
4)本文由校验系数、跨长以及施加的荷载计算结构的损伤程度虽有一定的截面限制,但无疑为开展此方面的研究起到一个抛砖引玉的作用。
[1] 宗周红,阮 毅,任伟新.既有桥梁承载力评估方法与展望[C]//中日结构减震与健康检测研讨会论文集,上海:2002.
[2] 交通部标准公路旧桥承载能力鉴定方法(试行)[S].北京:人民交通出版社,2004.
[3] 刘庆谭.材料力学[M].北京:机械工业出版社,2003.
[4] 刘 涛,杨风鹏.精通ANSYS[M].北京:人民出版社,1986.
[5] 盛和太,喻海良,范训益.ANSYS有限元原理与工程应用实例大全[M].北京:清华大学出版社,2006.
[6] 祝效华,余志祥.ANSYS高级工程有限元分析范例精选[M].北京:电子工业出版社,2004.
[7] 张献民,孙维丰,曹中杰,等.动态测试钢筋混凝土梁的新方法[J].工程力学,2002(S):616-619.
