一种加权的MCLP分类模型及其在不平衡数据集上的应用

朱梅红

（首都经济贸易大学 统计学院，北京 100070）

0 引言

在数据挖掘的分类问题中，经常出现数据集内类别不平衡现象。如信用卡客户识别、生产过程的故障检测等问题中，不同类别的样本数目相差很大：信用卡客户中“违约人”明显少于“守约人”，生产过程中“故障”状态通常少于“正常”状态。对于这些不平衡数据集，决策者更希望能够有效地识别出其中的少数类（以下简称小类）。

那么，如何在保证多数类（大类）分类正确率的前提下，提高小类的分类正确率？对于该问题的研究，可追溯到20世纪60-70年代[1-3]。随着海量数据分析的需要和数据挖掘领域的出现，该研究受到数据挖掘学术界的高度重视，从2000年开始已成为该领域研究的热点问题之一，对它的研究也变得更成体系和规模。

目前，针对不平衡数据的分类，有来自不同领域、针对不同现实问题、运用不同分类方法、从不同角度进行的研究。主要有三种思路：一是通过改进分类模型，使模型更关注小类；二是使用更合适的分类业绩评价标准；三是从训练数据入手，通过适当的数据处理技术，改变训练数据的类分布，以提高少数类的正确率。近50年来，基于第三种思路展开的研究，一直经久不衰。主要是利用抽样(或称再抽样)方法，达到训练数据类间的平衡。其中，抽样方法包括：(1)对小类进行随机上抽样，即通过随机复制小类内的样本点，以使训练集内各类样本量均衡；(2)对大类进行随机下抽样，即通过随机选择大类内的样本点，以使训练集内各类样本量均衡；(3)前两类基本方法的改进：有意识地增加或减少一些样本点[4-7]；(4)各种不同方法的结合运用[8]。比较而言，每种改进方法都有其合理的思想基础和实用价值。但是，没有一种方法是万能的。实际上，改进方法的效果，还取决于其他诸多因素，包括：分类器本身的特性，如，分类器对数据不平衡现象的敏感程度；数据集的特性，如，线性可分程度，类间交叠程度，数据不平衡的程度，训练集的大小；等等。

石勇教授提出的多目标线性规划(Multiple Criteria Linear Programming，以下（简称MCLP)[9-10]是一种比较年轻而优秀的线性判别分类方法，在学术界和应用领域已经取得了相当大的成功。但对于其在不平衡数据集上的表现，尚没有系统的研究。本文以二分类的信用卡客户数据集为例，根据MCLP的特性，从模型层面，提出适用于MCLP的不平衡数据处理技术，并对有效性进行实证分析。

1 MCLP分类模型

MCLP分类模型通过目标函数控制分类业绩，以约束条件作为判别准则。以信用卡客户数据集为例，一个两分类问题的MCLP模型为：

假定该数据集内的客户已经被分为两类，好人(Good，以下简称G)和坏人(Bad，以下简称B)，并且两类之间具有较好的线性可分性。对于客户i，可以用由r个预测变量构成的向量Ai来刻画，Ai=(Ai1,Ai2,…,Air)，i=1，2，…，n，n为信用卡客户数，即样本量。MCLP的思想是：希望求出一个系数向量X=（x1，...，xr）‘，和一个分类边界b（标量），由此构成一个线性判别式AX=b,以便把现有数据集内的两类客户分开，并对新的客户进行归类。对于客户i(表示为Ai)，通过计算其得分AiX，然后将其与b进行比较，以便对该客户进行归类。

为便于直观表示，假设“坏人”集合B在b的左方，“好人”集合G在边界b的右方。一般来说，数据集内的两类数据并不是完全线性可分的，所以它们有一定程度的重叠，如图1所示。在重叠区域，一些数据可能会被错误地分类。假设第i个客户被错误分类，记αi为点Ai到边界b的距离（即被错分的程度）；同理，假设第i个客户被正确分类，记βi为点Ai到b的距离。对于任一点Ai，它要么被正确分类，要么被错误分类，所以ai和βi中，至少有一个为0。所有被正确分类的点，有ai=0；所有被错误分类的点，有βi=0。因此两类客户符合以下等式所反映的条件。

MCLP的目标是同时要求最小化Sai和最大化Sbi。最初的MCLP分类模型表述为：

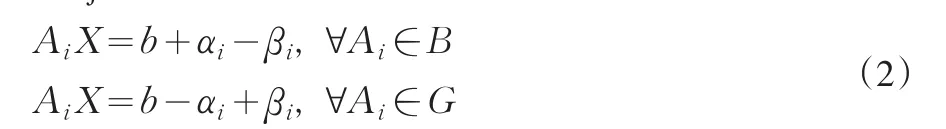
(M1)Minimizeand MaximizeSubject to:其中，Ai已知，X和b无约束,αi,0,bi,0,i=1,2,…,n M1的几何意义如图1所示：

对M1，也可以看作是同时要求最 大 化-Sai和 Sbi。而两个目标此消彼长，不可能同时达到最大。石勇等人[12]引入妥协解的概念，将问题转化为在两个目标之间寻求一个最优的折中，从而将多目标决策问题转化为单目标决策问题。

图1 带有重叠的二分类问题

假设-Sai的理想值为α∗＞ 0，Sbi的理想值为β∗＞ 0。利用妥协解的存在性，在-Sai和Sbi的关系曲线中寻找一个点A，使A点到理想点（α∗，β∗）的距离最短。这里，就是要求A点处的-Sai到α∗的距离与Sbi到β∗的距离之和最小。-Sai到α∗的距离就是妥协值-Sai与α∗的差距或称为遗憾，Sbi到β∗的距离就是妥协值Sbi与β∗的差距或称遗憾。因而新的目标函数就变成妥协解情况下两个目标的妥协值与理想值之间的差距或遗憾之和最小。具体来说，如此定义遗憾：如果-Sai＞ a*，定义遗憾为-da+=Sai+a*；否则，-da+=0。如果-Siai＜ a*，定义遗憾为da-=a*+Sai；否则da-=0。因此，总是有0。同理，有

M1进一步演化为单目标线性规划模型：

Minimize

Subject to

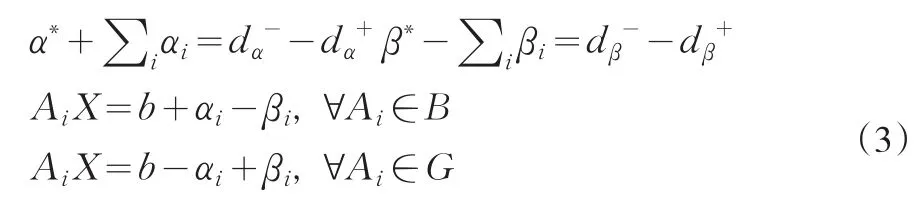
其中，Ai已知，X和b无约束,α∗和β∗给定

M2的几何意义如图2所示：

Min

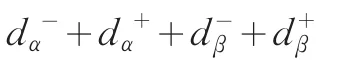
图2 基于妥协解的MCLP模型

作为一种线性分类模型，MCLP的原理简单易懂，易于计算机实现。尤其在计算时，可以灵活地修改参数b，α*，β*。另外，它是一种非参数方法，对数据不需要任何假设。从M2可以看出，要使目标函数达到最小，算法会自动寻找使Sai足够小和Sbi足够大的解。其中，为使Sai足够小，应同时使和足够小，但两者此消彼长，不能同时达到足够小；同理，为使Sbi足够大，应同时使和足够大，同样，和不能同时达到足够大。而在不平衡训练数据集内，两类数据规模不同。假定B类数目少，G类数目多，所以为使Sai足够小，模型在求解过程中，会倾向于忽略和的作用，强调和的作用，从而将小类错分为大类，使得小类错误率高于大类。由此可以看出，MCLP对两类数据样本量的比例（即类分布）比较敏感。

2 面向不平衡数据集的加权MCLP模型

本文基于MCLP模型本身，提出加权的MCLP分类模型，以改善小类的分类结果。该方法的基本思想是：假定训练集内小类和大类样本量分别为n1和n2（n1＜n2）,要求小类中的n1个样本点与大类中的n2个样本点在模型求解时发挥近似相同的作用，以达到两类数据分类结果的均衡。两类样本点在模型中发挥作用，是通过各样本点的αi和βi的取值实现的。这就需要在Sai和Sbi的组成中，两类样本点的力量比较均衡，即：在Sai中，；在Sbi中

这就是要求小类中的任何一个样本点，如果它被错分，其被错分的程度αi的作用要发挥至原来的n2/n1倍；同样，如果它被正确分类，其βi值的作用也要发挥至原来的n2/n1倍。通过修改M2模型中的一个约束条件，即可实现该目标。即：

将AiX=b+αi-βi,Ai∈B修改为：

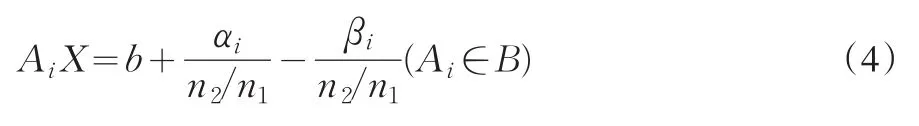
这里，用n2/n1代表小类中每个样本点的权数，因而将修改后的MCLP模型称为加权的MCLP模型。

该方法相当于对每个小类样本点，通过简单复制，形成n2/n1个样本点参与建模，本质上类似于上抽样。而与随机上抽样相比，该方法对小类样本点的复制更为均匀、全面。

3 实证分析

下面运用美国一家银行的信用卡客户数据集，说明该方法的有效性。

3.1 数据准备

经过整理，该数据集含有66个预测变量，5000条数据。由于其不平衡程度较严重（小类占16%），数据集较大，线性可分性一般，数据重叠严重（后两个特性可以从下面的分析中反映出来），因此该数据集很有代表性。首先将数据集随机分为训练池和测试集，并保证两者的分布相同。训练池是所有可用于训练的数据的集合，但建模时真正的训练集可能不同于训练池。各方法的效果用测试集上的分类结果来反映。为减少数据集分割的随机性产生的影响，对数据集进行3轮随机分割，用3轮随机分割的平均结果作为总的分类结果。同时，为使结果更具代表性，还要考察2种不同规模的训练集和测试集上的结果。分割结果见表1。

表1 信用卡数据集的分割

由于信用卡客户数据集的维数较高，不易直观显示两类样本点的分布情况。运用MCLP对其进行分类时，分类结果是满足M2模型目标函数的最优结果，因而，可以用M2的原始分类结果近似刻画两类样本点的分布情况。在模型求解时，设分界值b=1。

以第一轮分割形成的规模为3744（小类612+大类3132）的训练数据为例，运用MCLP M2对其分类，计算各样本点的分值AX，并观察各分值与判别边界b的关系。这里，相当于把66维空间中的每个样本点投影到一维空间中，而b则为该空间中的一个点，并作为两类样本点的分界限。从图3和4可以看出，两类样本点的分值都比较密集，由此我们推断两类样本点交叠比较严重。这里假定训练池和测试集的分布特点相同。如果仍按b=1作为分类界限，不论训练集还是测试集，小类的错误率都将接近60%，这是决策者所不能接受的。

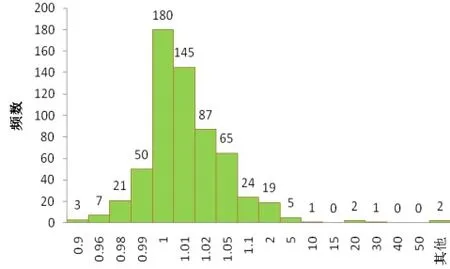
图3 3744个训练数据中小类样本点的分值分布图

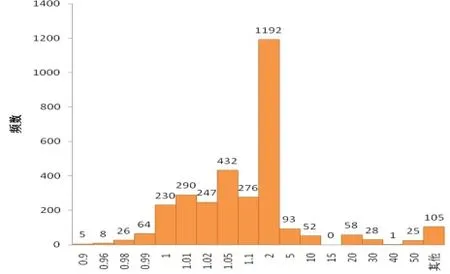
图4 3744个训练数据中大类样本点的分值分布图

3.2 加权MCLP模型中权数的设置

运用加权的MCLP模型时，训练集使用原始的类分布。在训练集样本量为1256和3744时，训练集内大类与小类的样本量之比均约为5.2，故在加权的MCLP模型中，每个小类样本点的权数n2/n1=5.2。

3.3 其他设置

为了显示本文所提出方法的效果，这里再运用两种基于数据层面的抽样技术：随机下抽样和随机上抽样。为了减少抽样随机性的影响，在进行下抽样时，对于每个比例、每一轮的分割，都从分割形成的训练池中，选取全部小类数据，对大类独立进行35次的随机下抽样，并保证两类样本量的平衡，形成该轮的35个训练集，并利用这35个训练集的解在测试集上的结果进行平均，最后再对3轮的结果进行平均。同样地，在进行上抽样时，对于每个比例、每一轮的分割，都从分割形成的训练池中，选取全部大类数据，对小类独立进行35次的随机上抽样，同时保证两类训练样本量的平衡，形成该轮的35个训练集，并利用这35个训练集的解在测试集上的结果进行平均。

3.4 各种改进方法的结果比较

为对不同方法进行比较，在模型求解和在测试集上进行判别分类时，判别阈值b统一设置为1。为了比较不同方法的综合分类结果，这里，也给出了各种方法在测试集上的AUC值。所有结果见表2。

可以看出，（1）根据原始类分布训练出的模型在测试集上的AUC值相对较高，这主要是由于训练集的分布和测试集的分布基本相同。但以b=1作为测试集上的判别界限时，小类的正确率太低。相对于原始类分布，其他四种方法对小类的分类结果都有很大提高。（2）运用随机下抽样技术时，小类的正确率较高，但大类的正确率相对较低，因而综合两类的结果，AUC值最低。这主要是由于小类样本量较小，因而大类中参与训练的样本点比例较低，代表性不足，大类存在信息丢失。（3）在随机上抽样中，由于小类点子是被随机选择并被复制的，可能出现的情况是，有的小类样本点被多次复制，而有的小类样本点则被复制的次数较少。如果小类中不幸存在被误标签的样本点或太多靠近边界的样本点，这些点被多次复制，就会不利于小类的分类结果。（4）相比而言，如果所有小类样本点被同等次数地复制，就不会过度夸大或缩小某个样本点的作用，训练集内小类样本点的分布与原始分布相同，能较好地代表小类数据，因而从AUC看，结果比随机上抽样和随机下抽样好。（5）运用原始类分布和加权的MCLP模型，本质上相当于将所有小类样本点均匀复制，所以其结果与第四种方法几乎相同。而与上述三种数据平衡方法相比，它不需要进行数据集的平衡处理，只需根据训练集的类分布（假定训练集和测试集的类分布基本相同），在模型中确定小类样本点的权数n2/n1。因此，不仅减少了数据操作的麻烦，而且与任何上抽样技术相比，其运算效率大大提高。

4 结论

本文分析了MCLP分类方法在不平衡数据集上的特性，提出了一种加权的MCLP模型，以减少数据集不平衡对MCLP分类业绩的影响。并以信用卡数据集为例，比较分析了几种不平衡数据处理方法对MCLP业绩的影响，显示了本文所提出方法的有效性和效率方面的优势。当然，本文只在一个数据集上进行了分析，未来还需要运用更多数据集来验证该方法的优势，并提出更多基于MCLP分类模型的不平衡数据处理方法。

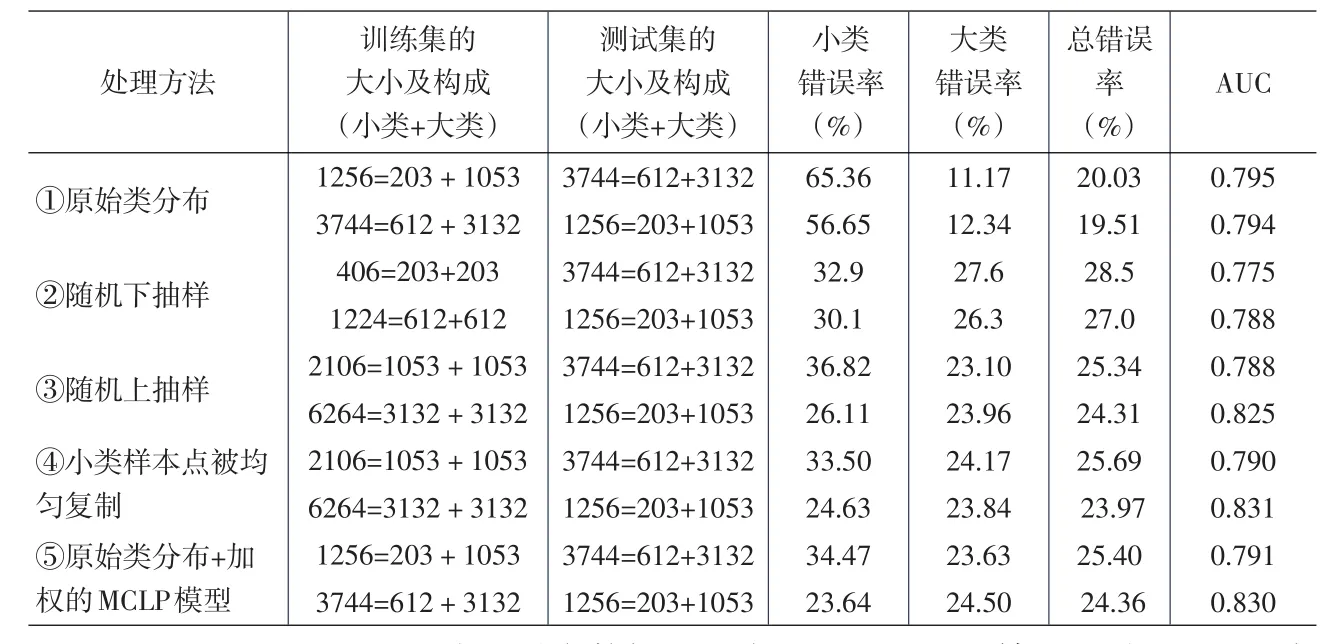
表2 各种方法在测试集上的分类结果比较

[1] P E Hart.The Condensed Nearest Neighbor Rule[J].IEEE Transactions on Information Theory,1968，(14).

[2] D L Wilson.Asymptotic Properties of Nearest Neighbor Rules Using Edited Data[J].IEEE Transactions on Systems，Man，and Communications，1972,(3).

[3] I Tomek.Two Modifications of CNN[J].IEEE Transactions on Systems Man and Communications,SMC-6,1976.

[4] M Kubat，S Matwin.Addressing the Curse of Imbalanced Training Sets:One-Sided Selection[A].Proceedings of the Fourteenth International Conference on Machine Learning[C].San Francisco：Morgan Kaufmann，1997.

[5] N V Chawla，K W Bowyer，L O Hall，et al.SMOTE:Synthetic Minority over-sampling Technique[J].Journal of Artificial Intelligence Research,2002,(16).

[6] C Phua，D Alahakoon,V Lee.Minority Report in Fraud Detection:Classification of Skewed Data[J].IGKDD Explorations,2 004，6(1).

[7] G H Nguyen,A Bouzerdoum,S L Phung.A Supervised Learning Approach for Imbalanced Data Sets[A].Proceedings of Nineteenth International Conference on Pattern Recognition[C].IEEE Computer Society,2008.

[8] G E Batista，R C Prati,M C Monard.A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data[J].SIGKDD Explorations，2004,6（1）.

[9] Y Shi，M Wise，M Luo，et al.Data Mining in Credit Card Portfolio Management:A Multiple Criteria Decision Making Approach[A].M Koksalan，S Zionts.Multiple Criteria Decision Making in the New Millennium[M].Berlin:Springer,2001.

[10] Y Shi,Y Peng,W X Xu,X Tang.Data Mining via Multiple Criteria Linear Programming:Applications in Credit Card Portfolio Management[J].Information Technology and Decision Making，2002,1（1）.