广义布尔函数的正规性

许广魁，杜炜



广义布尔函数的正规性

许广魁，杜炜

（淮南师范学院 数学与计算科学系，安徽 淮南 232001）

基于布尔函数的正规性，提出了广义正规Boolean函数的概念，给出了一些广义正规Boolean函数的构造方法，证明了广义正规Bent函数及其对偶函数所具有的一些独特性质.

广义布尔函数；广义Bent函数；正规性；有限域

1 引言和预备知识

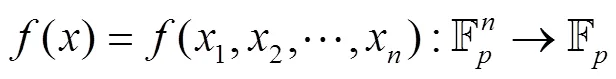
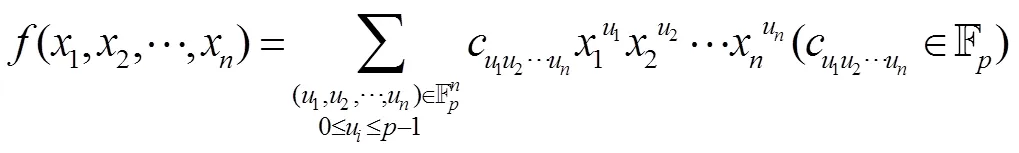
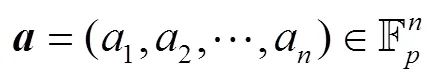
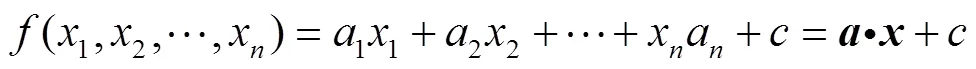
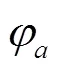
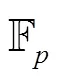
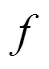
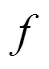
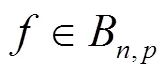
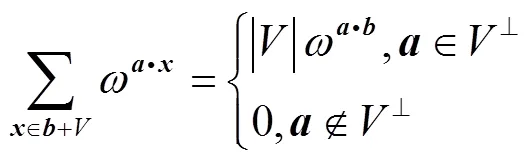
2 广义布尔函数的正规性

定义如下广义正规布尔函数作为对正规布尔函数的推广：

关于广义正规布尔函数和广义弱正规布尔函数，有下面的一个等价命题：

下面给出广义正规布尔函数的几种构造方法. 由例1可以得到：

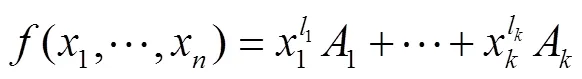
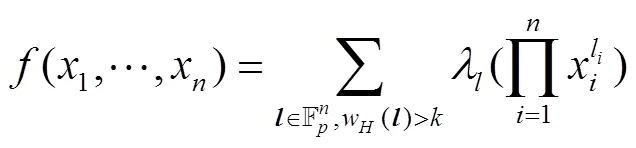
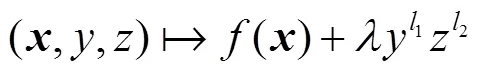
3 广义Bent函数的正规性

下面给出广义正规Bent函数所具有一些特有性质，研究广义Bent函数的正规性和对偶函数的正规性之间的联系.

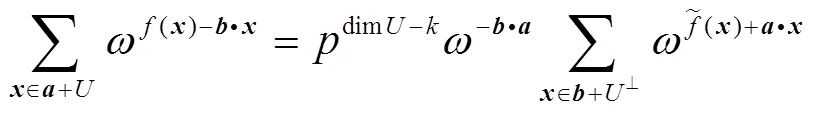
证明 由对偶函数的定义可知

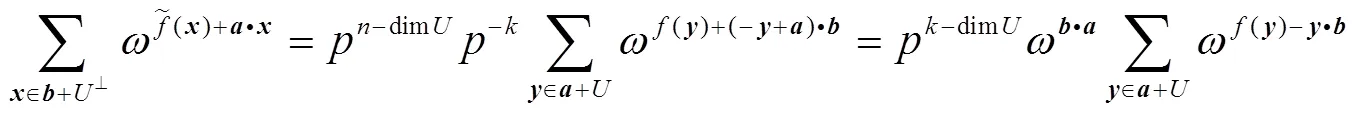
从定理5可以得到以下几个推论：

注：推论1表明如果一个广义Bent函数是正规的，则它的对偶函数也是正规的.

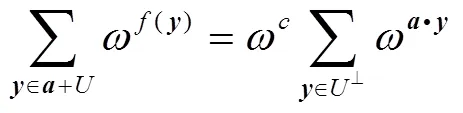
4 结束语

本文提出了广义正规Boolean函数的概念，讨论了广义正规Boolean函数的一些基本性质，给出了一些广义正规Boolean函数的构造方法，研究了广义Bent函数及其对偶函数的正规性. 同时，布尔函数的非正规性最近也成为研究热点，在以后的工作中，我们将探究广义布尔函数的非正规性，并试图用这种方法找到新的广义Bent函数.

[1] CARLET C. Two new classes of bent functions[C]//Advances in Cryptology–EUROCRYPT’93, Lecture Notes in Computer Science. Berlin: Springer, 1994: 77-101.

[2] DOBBERTIN H. Construction of bent functions and balanced Boolean functions with high nonlinearity[C]//Fast Software Encryption–FSE’94. Berlin: Springer–Verlag, 1995: 61-74.

[3] CHARPIN P. Normal Boolean functions[J]. Journal of Complexity, 2004, 20(2/3): 245-265.

[4] 冯克勤，刘凤梅. 代数与通信[M]. 北京：高等教育出版社，2005.

[5] 冯登国. 频谱理论及其在密码学中的应用[M]. 北京：科学出版社，2000.

On Normality of Generalized Boolean Functions

XUGuang-kui, DUWei

(Department of Mathematics and Computational Science, Huainan Normal University,Huainan 232001, China)

As a logical extension of the notion of normal Boolean functions, we focus on considering the normality of generalized Boolean functions. We present a method for constructing an infinite class of generalized normal Boolean functions. Then we give some consequences for the behavior of generalized normal Bent functions which are not included in generalized normal Boolean functions.

generalized Boolean function; generalized Bent function; normality; finite field

1006-7302（2011）02-0029-04

TN918.1

A

2010-09-07

安徽高校省级自然科学研究项目（KJ2011Z356）

许广魁（1981—），男，安徽宿州人，助教，硕士，主要从事代数组合论、信息可靠与安全研究.