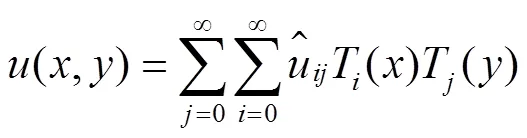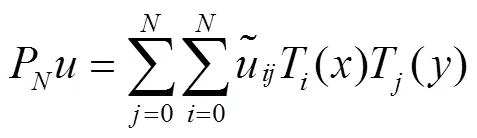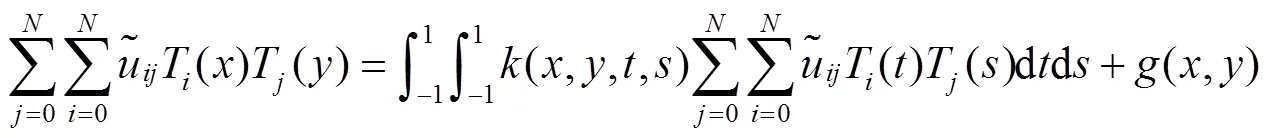一类二维Fredholm积分方程的Chebyshev配置方法和误差分析

李锋，王奇生



一类二维Fredholm积分方程的Chebyshev配置方法和误差分析

李锋，王奇生

（五邑大学 数学与计算科学学院，广东 江门 529020）

利用二元乘积型Chebyshev多项式作为基底，给出了一类二维Fredholm积分方程配置方法，并得到了相应的误差分析结果.

Chebyshev多项式；配置方法；二维Fredholm积分方程；误差分析

考虑下述二维Fredholm积分方程：

在解决Fredholm积分方程中，射影法具有运算次数相对较少、复杂程度相对较低的优点，而配置法又是射影法中一个较好的方法. 文献[1]用一维的Legendre多项式作基底，解决了一维Fredholm积分方程的Legendre配置法求解问题；文献[2]给出了二维Fredholm积分方程的Legendre配置解法；本文给出了二维Fredholm积分方程的Chebyshev配置法及误差分析.

1 Chebyshev配置法