L值P-下半连续函数

陈希西



值-下半连续函数

陈希西

（五邑大学 数学与计算科学学院，广东 江门 529020）

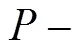
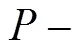
１ 预备知识

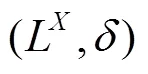
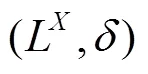
注：在F拓扑空间中，定义4就是文献[4]中相应的分离性定义.

2 L值P-下半连续函数

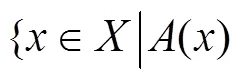
必要性.显然成立. 证毕.

证明 1）显然成立.

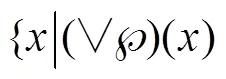
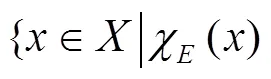
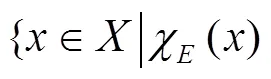
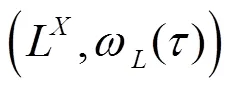
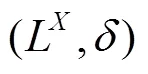
致谢 感谢导师白世忠教授的悉心指导.

[1] MASHHOUR A S, EI-MONSEF M E Abd, EI-DEBB S N. On precontinuous and weak precontinuous mapping[J]. Proc Math Phy Egypt, 1982, 53: 47-53.

[2]王国俊.-Fuzzy拓扑空间论[M]. 西安：陕西师范大学出版社，1988.

[3]韩明莲，谭燕华.-Fuzzy拓扑空间的-可数紧性[J]. 天津师范大学学报：自然科学学报，2002，22(2): 31-32.

[4] SINGAL M K，PRAKASH N T. Fuzzy preopen sets and fuzzy preseparation axioms[J]. Fuzzy Sets and Systems, 1991, 44: 273-281.

[6]白世忠. 拓扑分子格的弱分离公理[J]. 湘潭大学学报：自然科学版，1996, 18(1): 16-21.

-valued-lower Semi-continuous Functions

CHENXi-xi

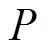
1006-7302（2011）02-0010-05

O189.1

A

2010-12-20

国家自然科学基金资助项目（61070150；10971125）；广东省自然科学基金资助项目（8152902001000004）

陈希西（1986—），女，湖南醴陵人，硕士研究生，研究方向为格上拓扑学.